T形柱正截面受力性能分析

王晓林

(太原学院基建处，山西 太原 030032)

0 T形柱正截面的力学特性

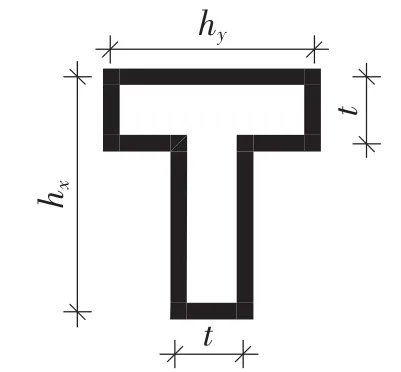
图1 T形柱正截面

当肢厚t=250mm时，分别变化它的腹板长度(hx－t)和翼缘长度hy，来分析两个垂直方向的刚度变化情况。通过计算[1]8－13，T 形柱正截面力学性能列表如下:

T形柱正截面x方向有一个对称轴，其形心在截面内，形心主轴与腹板边缘平行，等惯性矩条件下的T形截面面积比矩形截面面积要小，可以推断，T形截面比等面积矩形的刚度要大。因此，在符合抗震要求的前提下，优先选用异性柱的截面形式，可以节约材料，室内布局也整齐大方，有效利用了角部空间。两个垂直方向的尺寸相差越大时，相对于两个方向的刚度也相差较大，这样不利于抗震。在采用异形柱结构的实际工程中，应特别注意这一点。

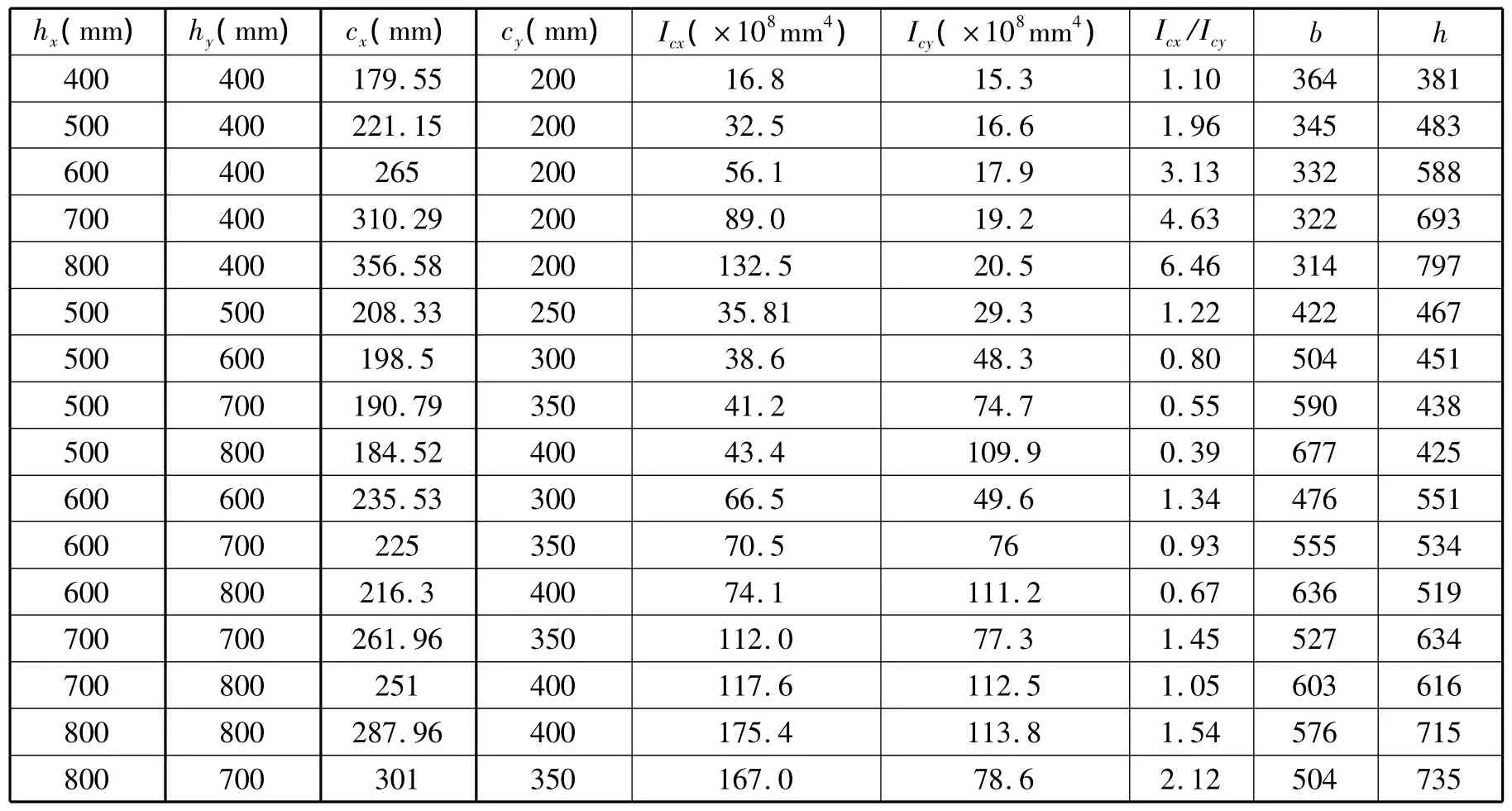
表1 T形柱正截面性能

1 体积配箍率对T形柱的影响[2]67－82

体积配箍率是用箍筋体积除以相应箍筋的一个间距包围的混凝土体积之后的比率来表示的。配箍率控制着混凝土构件斜截面绝大部分受剪承载力。为了构件不发生斜拉破坏和斜压破坏，控制结构构件斜截面的破坏形态，必须得有适当的配箍率才行。

实验模型的加载方式是柱顶位移加载，柱底的约束方式是悬臂固结。根据力的平衡，只要在柱顶加一个水平荷载即可，而这个荷载等于柱底剪力，然后将一个等截面的T形钢梁放于柱顶，单元号为beam188，高300mm，这样可以取得柱底剪力值，模型的网格划分为200mm×200mm×200mm。施加荷载时有两个荷载步，首先以面荷载的形式将轴向力加在整个表面，其次是在柱顶腹板底端中点施加水平位移，方向朝向坐标系Z轴正向。本实验模型是整体式的，SOLID65，这里假定此单元是连续、均匀，并且是采用各向同性的钢筋。整个单调荷载下非线性有限元计算过程，利用ANSYS软件，依托有限元理论完成。

1.1 承载能力变化

通过改变箍筋间距使得体积配箍率发生变化，间距分别是200mm、150mm和100mm。

表2 荷载对比

当箍筋间距变化后，三个变量:开裂荷载变化不大。屈服荷载、极限荷载都发生了明显的变化。当箍筋间距减小后，开裂荷载减小;屈服荷载降幅较大，极限荷载增大。体积配箍率增大后，使得试件提前屈服，但是延迟了试件的最终破坏时间，在发生地震时为人们争取逃生的时间。

1.2 变形能力变化

当体积配箍率增大后，极限位移增大，屈服位移减小，开裂位移保持不变。显然，箍筋的数量增多后，试件的延性改善很多。

表3 位移对比

2 轴压比对T形柱的影响

将轴压比分别为 0.3，0.5，0.7 的构件分别命名为 Z0.3，Z0.5，Z0.7。

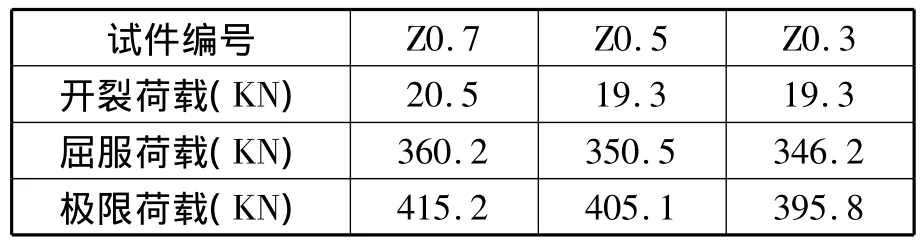
表4 荷载对比

表5 位移对比

表4说明，当轴压比减小，极限荷载、屈服荷载、开裂荷载都降低。表5说明开裂位移对轴压比的变化反应不大，屈服位移同轴压比的变化一致，但是极限位移增大，延性大大改善，说明随着轴压比的增加，T形柱的延性变差。

3 截面高厚比对T形柱的影响

异形柱截面的柱肢高与肢厚的比值(h:t)即为截面的高厚比，它可以用来区分异形柱、短肢剪力墙和一般剪力墙。本次实验中，全部试件均保持相同的相同的配筋率、相同的配箍率和相等的截面面积等，只有高厚比发生变化。依次是4.0、2.92、2.0，对应名称是大柱、中柱、小柱。

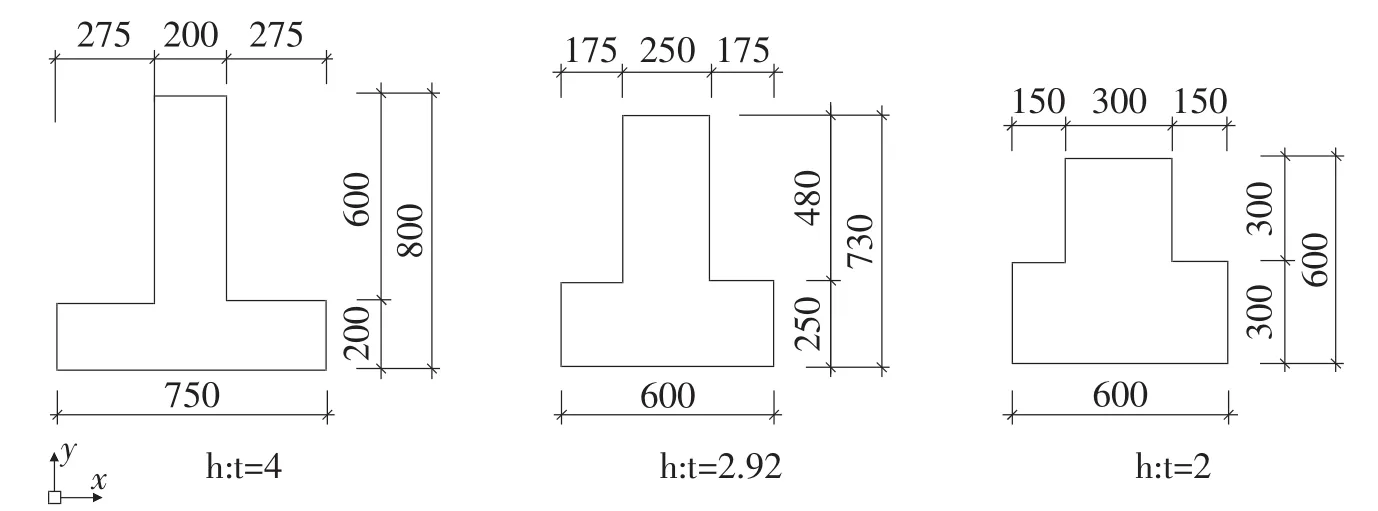
图2 异形柱截面尺寸

由于截面的惯性矩增大，抵抗变形的能力会增强。所以截面的高厚比减小时，开裂荷载、屈服荷载、极限荷载保持同其相同的变化趋势，高厚比是2.92的柱子截面延性最好。高厚比增大37.0%时，延性下降85.2%，衰减严重。所以我们在设计异性柱截面时，高厚比不宜过小，更不宜过大。

表6 荷载对比

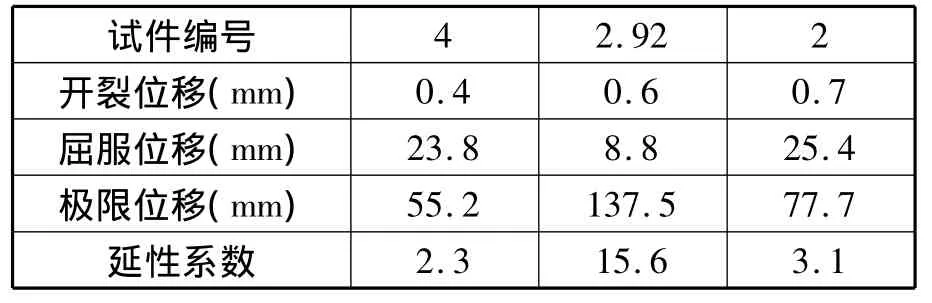
表7 位移对比

4 结论及展望

4.1 主要结论

本文利用ANSYS软件进行了T形柱正截面的受力能力分析。综上所述:

(1)对不同配箍率的T形柱的比较后，认为增大箍筋间距导致延性下降。

(2)对不同高厚比的T形柱的比较后，认为高厚比为2.92时的延性最好，高厚比不宜过大也不宜过小。

(3)轴压比改变时，柱肢的性能会产生变化。轴压比增大后，延性下降。

(4)三个实验中，裂缝发展规律基本是一致的。

4.2 有待以后研究的问题

本文对不同配箍率，不同轴压比，不同高厚比下的异形柱的性能进行了计算机模拟分析。如各项条件具备，最好是能完成实际试验的操作，这样结论会更有说服力。每一个领域都有无尽的科学需要我们去探索发现，关于异形柱有待进一步研究的课题还有很多，我认为急需研究的有:1、不同截面形式异形柱受力试验研究。如L形、十字形。2、不同材料异形柱抗震性能试验研究。如型钢混凝土异形柱。3、不同荷载作用下异形柱的受力性能。4、不同抗震等级下钢筋混凝土异形柱轴压比限值研究。5、高温下钢筋混凝土异形柱的截面特性等等。

[1]易金舫.形柱抗震受力分析及设计建议[D].西南交通大学，2007.

[2]王晓林.钢筋混凝土异形柱结构及其构件受力性能分析[D].太原理工大学，2011.