六自由度柔性测量臂关节零位偏差标定算法研究

胡 鹏 ，金国光 ，隋修武 ，郭振锋

（1.天津工业大学机械工程学院，天津 300387；2.天津工业大学天津市现代机电装备技术重点实验室，天津 300387）

六自由度柔性测量臂属于非笛卡尔式坐标测量机.它仿照人体关节结构，以角度基准取代长度基准，将6个杆件和1个测头通过6个旋转关节串联连接，一端固定在基座上，另一端（测头）可在空间自由移动，构成一个球形测量空间.由于其轻巧便捷、功能强大、使用环境要求较低、测量范围较广、投入成本较低，而被广泛地应用于航空航天、汽车制造、重型机械、轨道交通、零部件加工、模具制造等多个行业.尽管多关节柔性测量臂是一种非常有前途的便携式坐标测量臂，但测量精度低是其致命的弱点，这在很大程度上影响了它的应用.采用高精度的标定方法可以提高柔性测量臂的测量精度[1].多关节柔性测量臂的参数标定方法有很多，有基于最小二乘法和迭代算法[2-3]的参数标定，有基于遗传算法[4]的参数标定，有基于改进模拟退火算法[5]的参数标定等.本文首先建立了柔性测量臂的测量模型和误差模型，然后给出了用最小二乘法和迭代算法对六自由度柔性测量臂的关节零位偏差进行标定的方法，最后在Matlab中对标定算法进行了模拟仿真验证.

1 测量模型

六自由度柔性测量臂可以看成一个串联开式运动链，它是由6个杆件和1个测头通过6个旋转关节串接而成，图1为柔性测量臂简图.

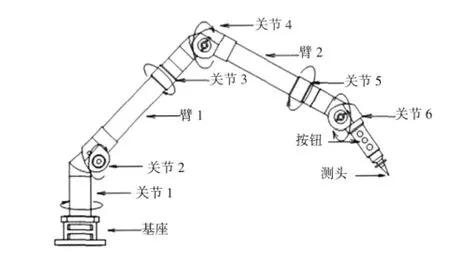
图1 柔性测量臂简图Fig.1 Schematic diagram of flexible measuring arm

Denavit和Hartenberg在1955年提出了对两个相互连接且相对运动的杆件之间相互关系的分析方法，简称 D-H 方法[2，4].

根据D-H方法，连杆i的坐标系的Zi轴位于连杆i与连杆i+1的转动关节轴线上；连杆i的两端轴线的公垂线为连杆坐标系的Xi轴，方向指向下一个连杆；公垂线与Zi轴的交点为坐标系原点Oi；坐标系的Yi轴由Xi和Zi按照右手定则确定，至此，连杆i的坐标系已建立.

测量臂的坐标系模型如图2所示.各杆件坐标系按D-H方法建立，由于在坐标转换过程中不用考虑Yi轴，在图2中未标出.图2中θ7所对应的旋转关节在接触式测量中不起作用，只在激光扫描测量时起作用，可以不用考虑.

在建立了各个杆件的坐标系之后，D-H方法规定用4个参数来描述杆件及杆件之间的关系，其中2个参数用来描述连杆，即连杆长度ai，连杆扭角αi；另外2个参数用来描述相邻两杆的关系，即两连杆距离di，两连杆夹角θi.

在建立了杆件坐标系并确定各个D-H参数之后，Oi-1Xi-1Yi-1Zi-1与OiXiYiZi之间的转换可以通过坐标系的平移、旋转来实现.转换矩阵如下:

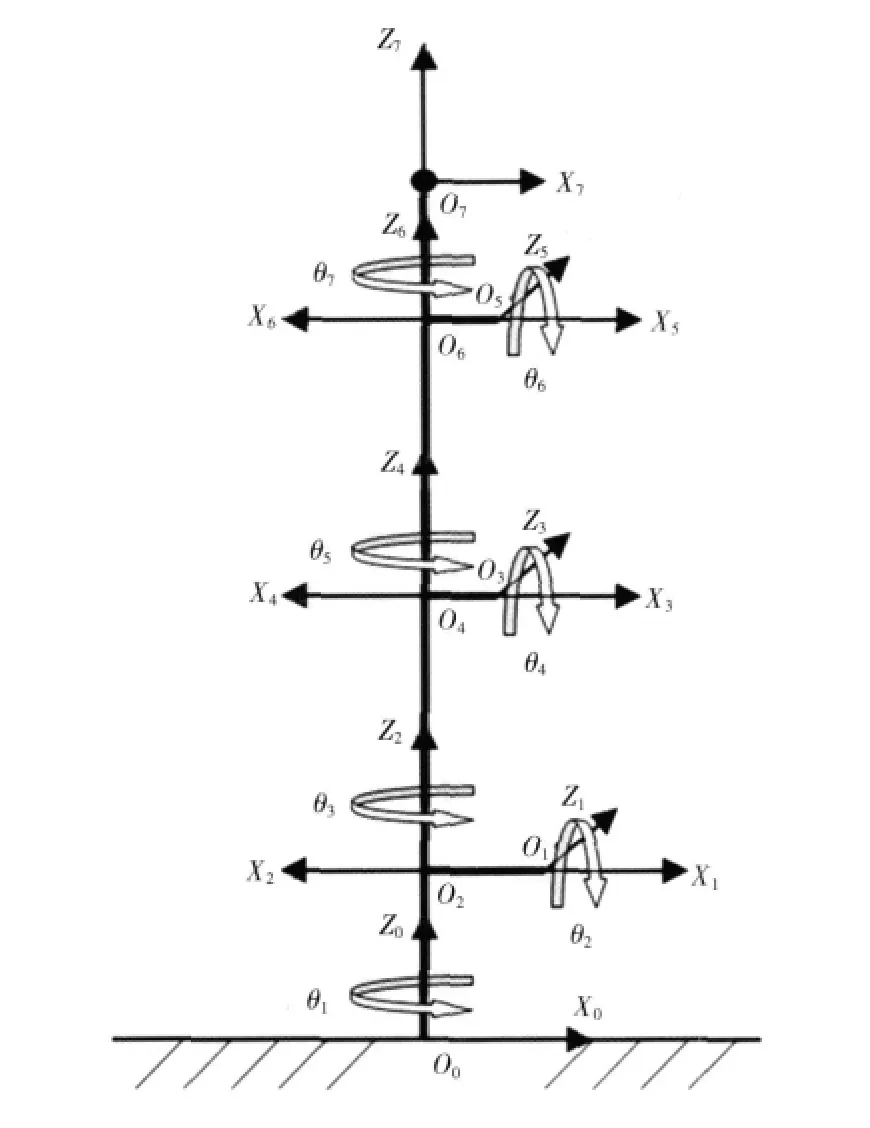
图2 测量臂的坐标系模型Fig.2 Coordinate system model of measuring arm

式中:Ri是3×3的旋转矩阵；qi是3×1的平移矩阵.

如图2所示，把测头坐标系O7X7Y7Z7相对于基座坐标系O0X0Y0Z0的位姿记为A07，这是一个4×4的齐次矩阵，由坐标转换关系可以得到:

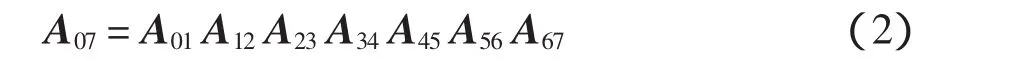
A07反映了测头在空间相对于基座坐标系的坐标位置与姿态.测头在基座坐标系下的齐次坐标P可表示为:

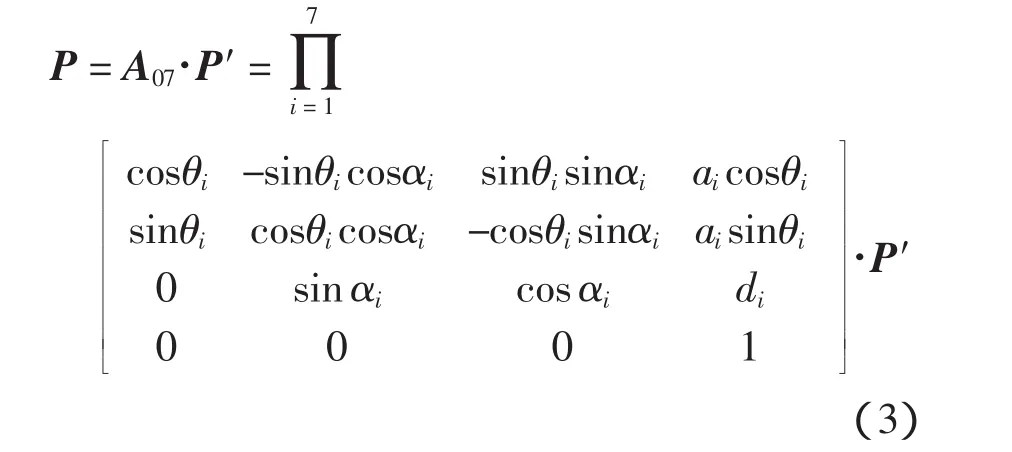
式中:P'=[0 0 0 1]T.

式（3）即为该六自由度柔性测量臂的测头位置坐标测量方程.杆件的 4个 D-H 参数中，参数 ai、αi、di都是固定的常数，称为杆件结构参数，而θi是变化的，称为关节变量.把测量方程写成矢量函数形式:

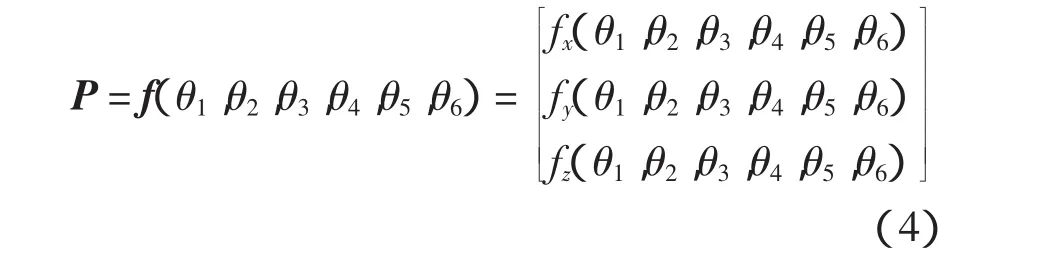
至此，六自由度柔性测量臂测量模型建立完毕.

2 误差模型

考虑到关节零位偏差对测量精度的巨大影响，首先建立基于关节零位偏差的误差模型.

关节零位偏差的特点:各关节的零位偏差互不相同；由于装配工艺水平所限，通常造成的关节零位偏差较大（约±3°），并且由于臂长的逐级放大作用，使得关节零位偏差在末端测头处产生很大的位置测量误差；对于每台装配好的关节臂式柔性测量臂，各关节的零位偏差固定不变，属于系统误差.

为了分析关节零位偏差对测量精度的影响，寻求关节零位偏差与测量位置误差之间的关系，假设关节零位偏差足够小.对式（4）进行全微分，近似得到测头位置误差方程[1-3]:

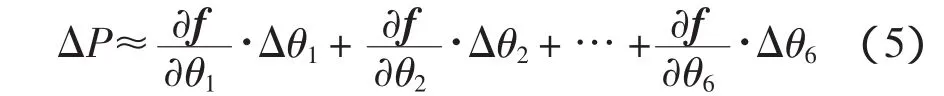
写成矩阵形式:

这里，ΔP=[ΔPx，ΔPy，ΔPz]T

Δθ是一个6×1的误差参数矢量，即:

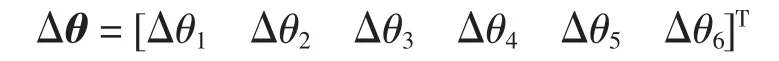
式（6）即为基于关节零位偏差的误差模型，它描述了关节零位偏差与测头位置误差之间的近似线性关系，这种线性关系的建立将大大地简化标定过程.

3 标定算法

通过提高柔性臂的角度编码器、机械零部件的加工与装配精度可以提高测量臂的测量精度，但提高的精度有限且成本非常高；此外，可以采取高精度的标定方法以提高测量精度.

基于最小二乘法和迭代算法的标定方法[2]如下:

为准确标定出关节零位偏差，需要一些已知的标准位置坐标，这些标准位置坐标可以通过高精度的测量设备获得.假设有m个标准位置坐标，用柔性测量臂测量这个m标准位置，记下这m组关节变量组合，然后把这m组关节变量组合代入式（3）计算出m个理论位置坐标，与标准坐标比对，可得到3×m个位置误差方程，即:

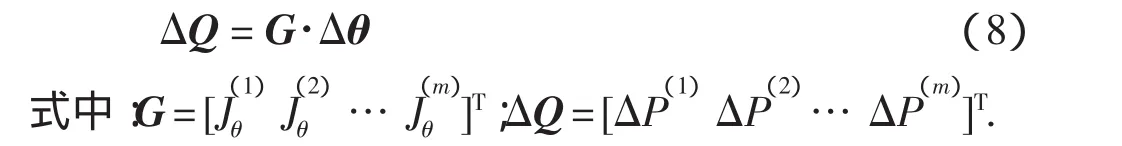
只要3×m＞6，则可运用最小二乘法解出6个关节零位偏差，即

把计算出的关节零位偏差作为修正值对式（4）中的关节变量进行修正，然后计算出新的位置误差和新的误差系数矩阵并代入式（8），再重复式（9）的计算，通过反复的迭代，直到测头位置误差满足要求，从而获得最佳标定结果.

4 仿真验证

为了进行计算机仿真，首先给定柔性臂的结构参数，并假定关节零位偏差.具体数值如表1所示.

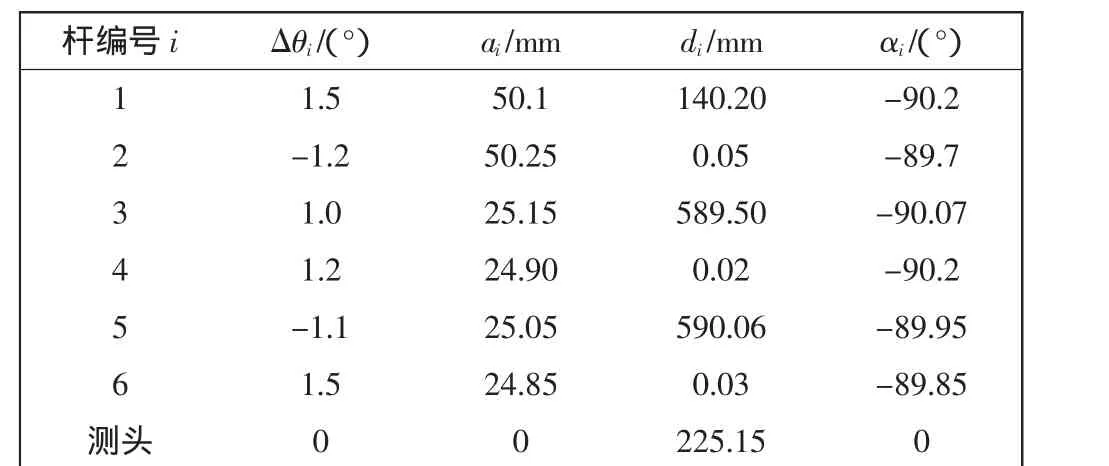
表1 柔性测量臂结构参数Tab.1 Structural parameters of flexible measuring arm

为了验证该标定算法的正确性，共做了3组模拟实验，每组实验包含3组关节变量组合，标定过程分以下3步:

第1步:根据表1中的结构参数和关节零位偏差，按式（3）计算出3个实际的空间坐标作为标准坐标Pb.然后不考虑零位偏差，计算出3个理论坐标Pl，从而得到位置误差矢量ΔP=Pb-Pl.

第2步:根据式（7）计算出误差系数矩阵，然后根据式（9）运用最小二乘法计算出Δθ.

第3步:将第2步得到的Δθ作为修正量对关节变量的理论值进行修正，计算出新一轮的坐标理论值，误差系数矩阵和位置误差矢量.如果修正后位置误差矢量满足要求则结束，未达到要求则重复式（9），计算出新的Δθ，在前一次修复的基础上继续对关节变量进行修正，计算修正之后的位置误差，直到满足要求为止.

本次模拟仿真经过2次迭代，结果如表2所示.

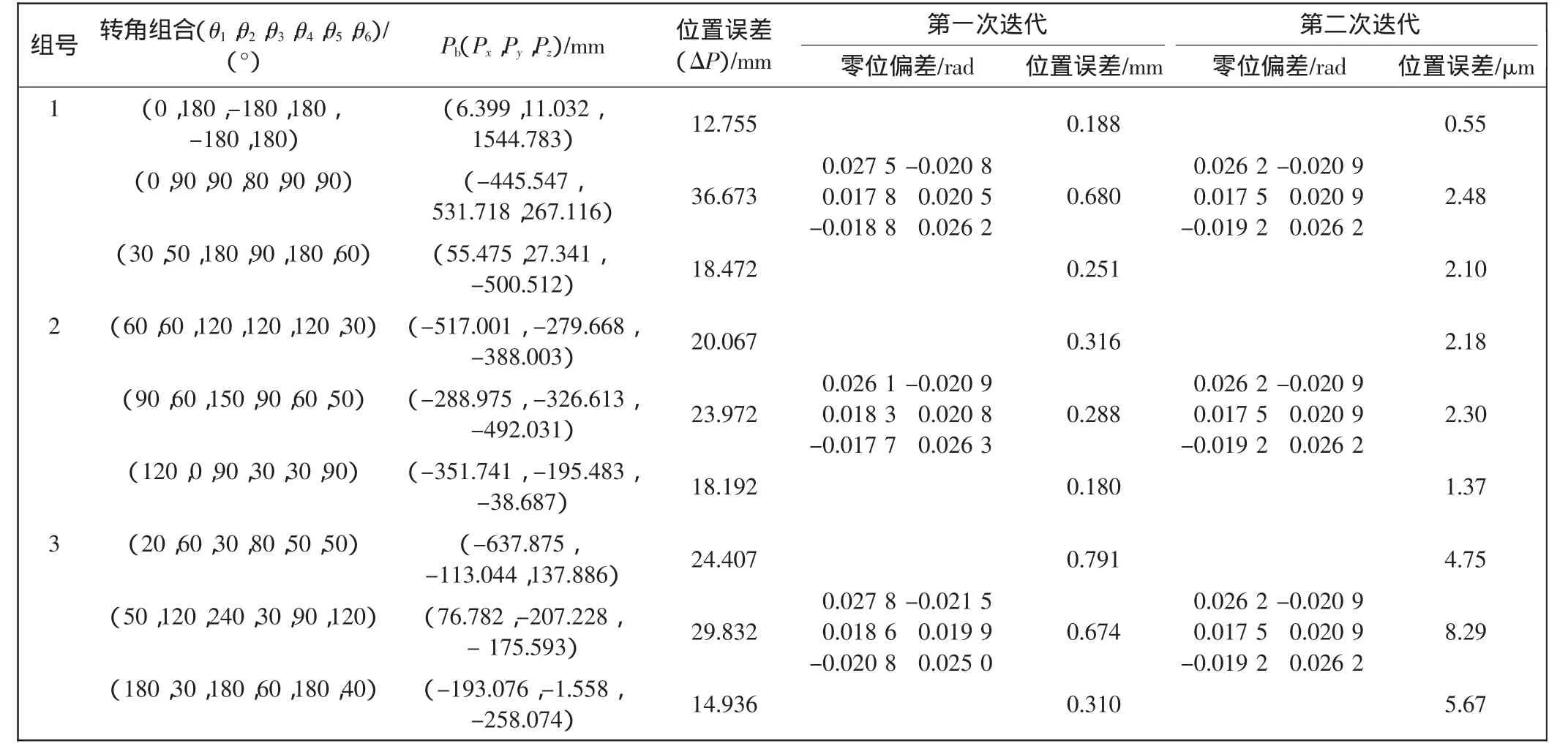
表2 仿真结果Tab.2 Simulation results

由仿真结果可知:

（1）较小的关节零位偏差通过臂长的放大作用会造成很大的位置测量误差，达到数十毫米.

（2）经过一次最小二乘标定，即可把位置误差减小到1 mm以内，经过第二次最小二乘标定，基本上可以消除位置测量误差.

（3）之前设定的关节零位偏差为（1.5°，－1.2°，1.0°，1.2°，－1.1°，1.5°），转化为弧度制表示为:（0.0262，－0.0209，0.0175，0.0209，－0.0192，0.0262），这与仿真验算结果是吻合的，由此可知，通过该标定算法可以准确地标定出关节零位偏差的真实值.这也间接地论证了误差模型的正确性.

（4）3组实验得到的结果相同，说明只要在测量空间任取3点，即可准确且惟一地标定出6个关节零位偏差.

5 结论

本文在建立了六自由度柔性测量臂的测量模型的基础上，运用全微分法建立了基于关节零位偏差的线性误差模型.然后，利用该线性误差模型，结合最小二乘法和迭代算法建立了关节零位偏差的线性标定模型.该标定模型的优势在于，将复杂的非线性参数辨识问题线性化，大大简化了标定过程.最后，通过Matlab模拟仿真验算，证明了该标定算法的正确性.该研究对提高柔性测量臂的测量精度具有重要意义，也为自主研发高精度多关节柔性测量臂提供了理论支持.

[1]王春花，费业泰.柔性三坐标测量机的结构系统及误差修正标定分析[J].工具技术，2006，40（9）:76-78.

[2]魏霖，王从军.多关节坐标测量机的坐标转换和参数标定[J].光电工程，2007，34（5）:57-61.

[3]汪平平，费业泰，尚平，等.柔性坐标测量机参数辨识方法[J].农业机械学报，2007，38（7）:129-132.

[4]邹璇，李德华.多关节机械臂的坐标模型和参数标定[J].光学 精密工程，2001，9（3）:252-256.

[5]高贯斌，王文，林铿，等.应用改进模拟退火算法实现关节臂式坐标测量机的参数辨识[J].光学精密工程，2009，17（10）:2499-2505.

[6]WANG Xueying，LIU Shugui，ZHANG Guoxiong，et al.Calibration technology of articulated arm flexible CMM [J].Journal of Harbin Institute of Technology，2008，40（9）:1439-1442.