基于蠕变特性的加筋挡土墙有限元分析

张佳佳，蔡良才，刘一通，刘 伟

（1.空军工程大学 机场建筑工程系，西安 710038；2.空军工程设计研究局，北京 100068）

加筋土挡墙的主要组成部分分别是面板、填料与筋材，这三种材料组成了相互协同作用的整体。加筋土挡墙的结构特性与其组成材料的工程力学特性和不同材料之间相互作用的机理具有紧密的联系。土工合成加筋材料是加筋土挡墙中应用最为广泛的筋材，作为一种新型的土工聚合材料，具有排水、反滤、隔离、加固、保护与防渗等六个方面的作用，具有良好的经济型、安全性以及施工的简便性。土工合成加筋材料通常为高分子聚合物，最具典型的是土工格栅。土工格栅在土体中一般处于受拉状态，在一定温度下，土工格栅在受到长期的拉力作用下会发生蠕变现象，这种蠕变通常与土工格栅自身的材料特性相关，并可能导致加筋土结构发生变形与强度减小的情况，最终可能导致加筋土结构的失效。

目前，关于土工合成加筋土结构的研究一直是学术界研究的重点，大部分学者通过有限元数值分析方法进行研究，往往认为筋材与土体是相互分离的两个部分，通过在筋材与土体之间的接触面上设置界面单元来分析两者的相互作用与变形[1-5]。Harrison[1]认为加筋土体为各向同性的复合材料，他在这个前提下建立了加筋土体的应力与应变关系。A.Sawikci[2]认为加筋材料与土体之间不会发生相互的位移，并将认为其满足Mohr-Coulomb破坏准则的理想塑性材料，在此基础上建立了加筋土刚塑性模型。以上研究均没有考虑筋材的蠕变性能。

笔者针对以上研究的不足，提出了蠕变性能的加筋土蠕变模型，分析了考虑加筋材料发生蠕变情况下受固定载荷作用的蠕变变形特征。将本文的计算结果与传统的计算方法、实际测量数据进行分析比较后发现，本文所提出的研究方法具有可行性。

1 基于蠕变特性的加筋土本构模型建立

1.1 基本假设

本文假设如下：加筋土为宏观上均匀的各向异性的复合材料；加筋材料为土工格栅，视为黏弹性材料；土体为满足MohrCoulomb准则的弹塑性材料；认为加筋材料与土体之间并不发生相对滑动。加筋材料结构的宏观应力为σij，整体的应变为εij。

1.2 三参数黏弹性模型的应用

对于一般的加筋结构中，加筋材料受到的载荷属于低应力水平载荷。根据相关文献[4]可知，当加筋材料受到的载荷较小时，可以将土工格栅蠕变分为两种模式：初级减速蠕变模式与二级衰减蠕变模式，如图1所示。笔者认为可以将土工格栅在长期受到较低载荷下所发生的蠕变现象所显示的黏性特性通过三参数黏弹性模型进行表示，如图2所示。

通过受力与变形分析，可以得到最终应变结果如式（1）所示。

图1 蠕变过程示意图

图2 三参数黏弹性模型示意图

式中：σ，ε分别为加筋材料受到的应力与应变；E1，E2为模型中弹簧的刚度系数；η为黏壶的黏滞系数；t为时间。

笔者基于三参数黏弹性模型，建立了加筋土的本构模型，所提供的方法可以使土工格栅的蠕变应变成为加载应力与时间的函数，从而简化了分析过程。通过这一模型可以得知在加筋材料受力的瞬间，弹簧元件会发生形变，但是Kelvin体来不及发生形变。随着时间的增加，Kelvin体开始发生变形，整个土工格栅的蠕变将逐渐变得稳定。

笔者针对式（1）所示的蠕变模型进行了实验验证。其中为了进行蠕变模型的验证，先测量得到了土工格栅的相关数据，如表1所示。

表1 土工格栅的相关参数

加筋材料在不同的应力条件下蠕变模型验证试验如图3所示。根据试验结果显示，在低应力载荷作用下，加筋材料刚开始的蠕变形变迅速增加，随后出现应变斜率下降的现象，也就是说应变的增加速度逐步放缓。最终蠕变形变量逐渐稳定下来，出现上文所述的衰减形变的特征。从蠕变模型验证试验中可以看出，本文所提出的三参数黏弹性模型符合试验结果。

1.3 加筋土本构模型建立

由式（1）可以推导得到公式（2）。

图3 蠕变模型验证试验

在本文中定义压应力方向为正方向，也就是说当加筋材料在受到拉力作用时，作用力为负，而产生的形变量也为负值。定义加筋材料的厚度为e，则加筋材料层应力σ与加筋材料单位宽度上拉力R）的关系如式（3）所示。

将式（3）与式（2）结合，可以得到土工格栅黏弹性本构模型的另外一个表达形式，如式（4）所示。

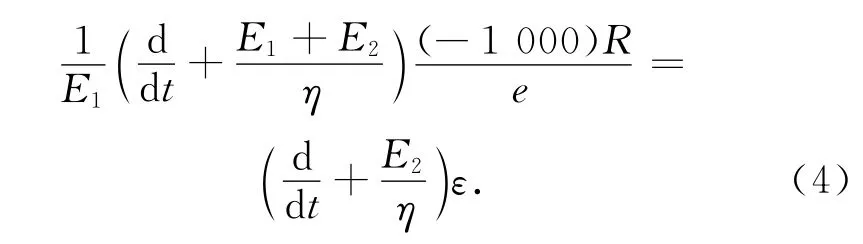
在本文中，认为加筋土结构的宏观应力与应变同土体与加筋材料的微观应力以及应变存在以下关系式：

式中：σij（s）与σij（r）为 土 体 微观应力与 应 变；εij（s）与为筋材微观应力与应变；n与Δh分别为加筋材料土工格栅体积含筋率与层间距。

在平面应变条件下，土体处于弹性阶段时，有以下关系：

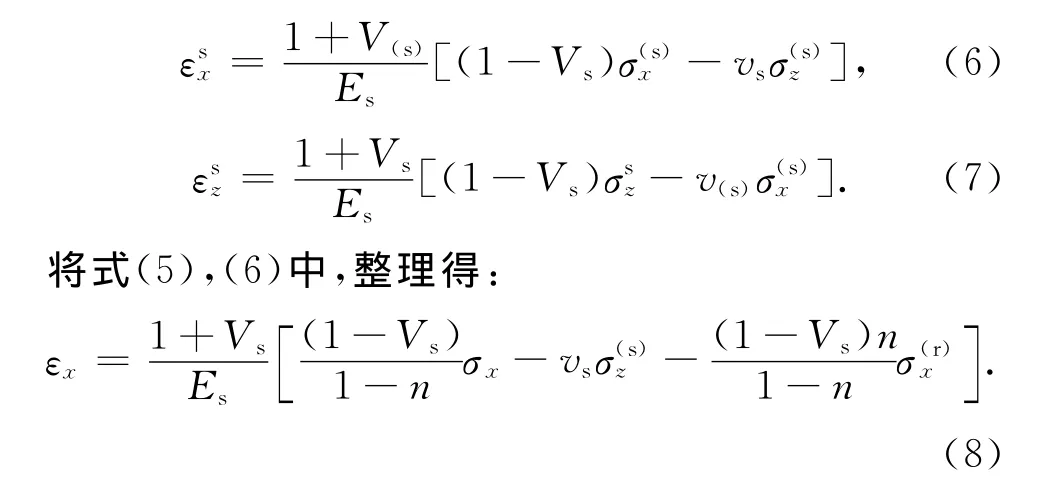
一般认为加筋土结构中含筋率n很低，所以n≈0，在这一条件下，可以将式（8）化简为：

式中：R0为加筋材料起始状态单位宽度拉力；t小于加筋土塑性状态达到的时间。

当土体处于塑性状态时，加筋材料所受应力保持不变，可由式（4）与式（7）得到式（18）：

通过求解微分方程式（13），可以得到当土体处于塑性状态时，加筋土的应变公式：

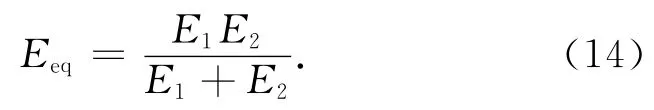
至此，已经得到了加筋土弹性与塑性阶段的加筋材料与土体结构的应力与应变表达式。通过分析可以看出，加筋材料的应力不仅与加筋土的受力有关，还与加筋材料的特性、加筋层间距与土体的特性等相关。

2 有限元模拟分析

2.1 有限元非线性计算方法

在有限元分析中所用的非线性计算方法采用了动态松弛法，由于该方法在进行求解非线性方程问题方面具有较为明显的优点，非常适用于具有高摩擦角的土体。本文计算时，结果的收敛状态有以下两个标准进行判定，如式（15）与式（16）所示。

1）整体残余应力相对标准

2）两次相邻迭代（n和n＋1）间整体残余力绝对标准

其中P为内力矢量；Pinit为初始应力引起的节点力矢量；F为外力矢量；为了保证非线性计算的有效收敛，有限元计算过程中取εF＝εD＝10-6。

除了以上所述，由于土体具有高度的材料非线性，为了改进这一问题在准平衡状态下解的跳跃问题，在本文的有限元求解过程中采用了缩减积分。对于有限元计算中的四边形单元的沙漏现象，通过利用弹性刚度法控制沙漏，也就是在任何土体单元发生沙漏现象时，将加载开始时真实的材料刚度附加在非线性系统中作为抵抗沙漏的节点力。

2.2 有限元模拟分析结果

笔者根据工程实际建立模型，如图4所示。在进行有限元计算时，初始应力场中垂直应力为σv0＝γdh，水平应力为σh0＝K0σv0，其中h为相应单元的高斯点距离顶面的深度，模型试验中沙土的容重比γd为16.0kN／m3，一般认为K0为0.34。

图4 有限元计算模型

根据前面所述，认为与基底相接触的节点均没有水平方向的位移。蠕变加载采用载荷控制法，蠕变时在相同节点上施加恒定的节点力。在进行有限元分析时，基底压力q与基础沉降s分别选取基础正下方10个单元的相应高斯点上垂直应力与迟滞位移的平均值。土体单元水平方向的应力为17.0kPa；格栅加筋材料水平方向的单元应力为＝-7.00kPa；加筋单元宏观初始竖直方向的应力σz为51.0kPa，水平方向的应力σx为10kPa。通过有限元计算可得到达塑性状态前土工格栅单元和土体单元应力在不同时刻的数值，基底压力q与基础沉降s的相互关系，并通过与实际试验的结果进行比较，如图5所示。

可以看出有限元模拟的结果与试验结果在沉降速率发生突变时与基底压力比较接近，而且各个解决的蠕变特征也具有一定的吻合度。加筋土在达到塑性状态之前，由于应力松弛，随着时间的推移，加筋格栅所受拉力与土体应力逐渐减小，随着时间接近加筋土塑性状态达到时间tp，加筋格栅单元应力和土体单元应力趋于稳定。

图5 土工格栅单元和土体单元微观应力的变化

3 结论

本文的研究把加筋土体看成一个整体，分为两个阶段来考虑，第一阶段为黏弹性阶段，第二阶段为黏弹塑性阶段。随着时间的推移，加筋材料发生按负指数衰减的应力松弛，筋材的应力降低，应变增加。加筋材料的应力降低引起土体结构的应力减小，产生加筋材料与土体之间的应力重新分布。当土体达到屈服条件时弹性阶段结束，开始进入塑性阶段。在黏弹塑性阶段，加筋体中应力保持恒定，整个应变由于蠕变的发生逐渐增加。总体而言，本文考虑了筋材蠕变特性的因素，给出了加筋土体整个过程中的应力-应变关系，可以针对具体的工程例子分析加筋土体的应力和变形情况，尽量减轻由于加筋土体强度、稳定性降低、变形增加造成的严重后果。

[1]HARRISON W J，CLARLES M G.Elastic theory applied to reinforced earth[J].Journal of the Soil Mechanics and Foundation Division，1972，98（12）：1325-1345.

[2]SWAIKCI A.Plastic limit behaviors of reinforced earth[J].Journal of Geotechnical Engineering，1983，109（7）：1000-1005.

[3]SAWICKI A.Rheological model of geosynthetic-reinforced soil[J].Geotextiles and Geomembranes，1999，17（1）：33-39.

[4]陈群，朱分清，何昌荣.加筋土本构模型研究进展[J].岩土工程技术，2003（6）：360-363.

[5]HUANG B Q，BATHURST R J，HATAMI K.Numerical study of reinforced soil segmental walls using three different constitutive soil models[J].Journal of Geotechnical and Geoenvironmental Engineering，2009，135（10）：1486-1498.

[6]TAECHAKUMTHORN C.Effects of reinforcement and soil viscosity on the behaviour of embankments over soft soil[D].Kingston：Queen′s University，2011：96-103.

[7]HSIEHL C W，LEE K，YOO H K，et al.Tensile creep behavior of polyester geogrids by conventional and accelerated test methods[J].Fibers and Polymers，2008，9（4）：476-480.

[8]栾茂田，肖成志，杨 庆，等.土工格栅蠕变特性的试验研究及黏弹性本构模型[J].岩土力学，2005，26（2）：187-190.

[9]肖成志，栾茂田，杨 庆，等.土工格栅经验型蠕变模型及其参数试验[J].中国公路学报，2006，19（6）：19-24.

[10]周光泉，刘孝敏.黏弹性理论[M].合肥：中国科学技术大学出版社，1996：8-27.

[11]李董辉，童晓娇.数值最优化[M].北京：科学出版社，2005：174-180.