浅谈高考中的构造函数法
●
(台州中学 浙江临海 317000)
浅谈高考中的构造函数法
●翟美锁
(台州中学 浙江临海 317000)
函数是中学数学的重要内容,函数思想渗透到高中数学的每一个知识板块,是历年高考的必考内容.引导学生学会应用构造函数解决一些数学问题,不仅为解题提供了一个有效的方法,而且能加深学生对函数的认识.笔者结合近几年的数学高考题以及模拟题,探讨构造函数的方法和技巧.
1 细心审题,留意铺垫——等价转化法

(1)求f(x)的单调区间;

(2008年安徽省数学高考理科试题)





即
m>-eln2.

2 选定主元,巧妙构造——主元法
在许多数学问题中,都含有常量、参量、变量等多个量.通常情况下,有一些元素处于突出和主导地位,可视之为主元.为了解决问题,也可人为突出某个量的地位作用,先将其当作主元,从而进一步把握解决该问题的主元.
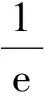
(1)求b,c的值及f(x)的单调递减区间;
(2)设p>0,q>0,g(x)=f(x)+x2,求证:

(2013年浙江省六校联考数学试题)

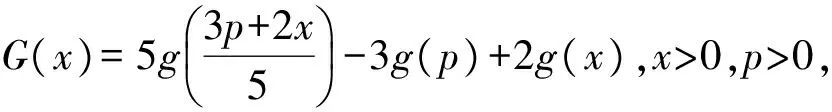
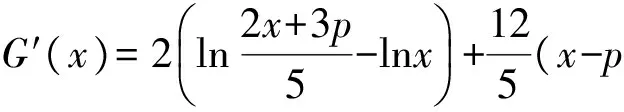

又因为G(p)=0,所以G(x)≤0,即
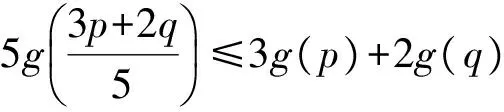
点评一方面,遇到含多元问题时,主元策略往往带给我们启发,化多元问题为一元问题,体现了化归转化思想;同时,主元策略还表现于主元选择的变通性,选择不同的主元,对于结构不对称的式子能形成不同的解题途径.
3 结构整齐,多变量问题——减元法

(1)讨论函数的单调性;

(2009年辽宁省数学高考理科试题)
分析由于第(2)小题中的不等式结构对称整齐,可作如下变形:
设x1>x2,f(x1)-f(x2)>x2-x1,即f(x1)+x1>f(x2)+x2,若构造函数g(x)=f(x)+x,即等价于证明函数y=g(x)的单调性.
解(1)略.
(2)考察函数
g(x)=f(x)+x=

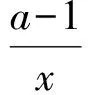

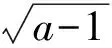
由于1
f(x1)-f(x2)+x1-x2>0,
于是
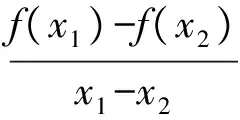
当0 点评本题利用不等式的对称性,把含2个变量的问题转化为函数(1个变量)的单调性,后面的证明较容易. 例4设a>0,b>0,e为自然对数的底数, ( ) A.若ea+2a=eb+3b,则a>b B.若ea+2a=eb+3b,则a C.若ea-2a=eb-3b,则a>b D.若ea-2a=eb-3b,则a (2012年浙江省数学高考理科试题) 分析ea+2a=eb+3b,等式结构不对称,因此无法与函数的构造联系起来,但是该等式可以利用适当的放缩来实现对称从而达到构造的目的. 考察选项A,B,因为ea+2a=eb+3b>eb+2b,所以 ea+2a>eb+2b. 记f(x)=ex+2x,由于f(x)在R上单调递增,因此a>b,正确答案为A. 点评局部对称的条件可以通过适当的改进(比如放缩法)转化为条件对称. 构造函数法通过研究函数的单调性,体现了数学中函数、化归的思想,其中也渗透着猜想、探究等重要的数学思想.通过研究近几年的高考题发现,构造函数的题目几乎都在压轴题上,可见难度很大,因此要熟练地掌握函数的性质,灵活地应用数学知识,才能合理地构造出函数. [1] 宁桂华.构造函数法解决导数问题的研究[J].数学学习与研究,2012(21):10-11. [2] 武增明.构造函数证明函数背景下的不等式的策略[J].中学数学,2012(15):7-8.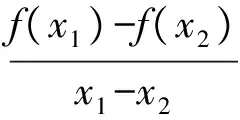

4 联想迁移——放缩法

