问题链驱动下的探究式教学
——“任意角的概念”教学设计评析
●
(小海中学 江苏南通 226015)
问题链驱动下的探究式教学
——“任意角的概念”教学设计评析
●黄锋
(小海中学 江苏南通 226015)
三角函数是描述周期现象的重要数学模型,三角函数一章的研究,从具体问题入手,以问题为背景,体现了“问题情景―建立模型―解释、应用与拓展”的过程.“任意角”是三角函数的第一课,是在锐角、直角、钝角,平角、周角的基础上,对角的概念进一步推广.本节课需要解决好以下几个问题:首先是推广角概念的必要性;其次是正角、负角、零角、象限角、轴线角以及终边相同的角等概念建构的自然性、合理性;再次是对终边相同角的集合的表示及判断象限角等知识运用环节中难点处理的巧妙性.理解任意角的概念,会在平面内建立适当的坐标系,通过数形结合来认识角的几何表示和终边相同角的表示,是学好本课的关键.
为了调动学生的学习兴趣,本节课从学生熟悉的生活情境入手.为了使学生能够轻松地理解看似零碎的概念,本节课借助类比,引导学生观察、思考并感悟概念的本质.为了使学生深刻理解难点,本节课借助生活中的时钟模型,通过设疑来激发学生的思维,通过学生自己动手、体会、归纳,从而解决难点.整节课以问题链的形式展开,通过层层设问,引导学生自主发现问题,自主解决问题;学生探究性学习活动贯穿于整个解决问题的始终.本文主要从3个方面结合教学设计来谈谈笔者对“任意角的概念”教学实施过程中的一些认识.
1 优化数学情境,自然引出课题
课堂教学中,教师有目的、有意识地引入或创设具有一定情绪色彩、以形象为主体的、生动具体的情境,可以使所有的学生都参与到数学学习中来,激发每一个学生的学习热情和学习兴趣,帮助学生更好地理解教材.本课教学安排了学生非常熟悉的摩天轮的例子,具体内容如下:
情境游乐园是人们爱去的地方,各种神奇的游戏器械吸引着人们去玩耍,高大的摩天轮绕轴转动着,边缘上悬挂的座椅,带着游人在空中旋转,给游人带来乐趣!星期天小明的父母带小明到游乐园玩,父母让小明独自一人乘坐摩天轮(摩天轮20分钟转一圈),而父母分别站在摩天轮的2侧.
问题1小明坐上最底部的一个座椅,第5分钟时,摩天轮转动多少角度?第10分钟呢?第1次回到起点时呢?第2次回到起点时呢?
问题2720°是怎样的一个角呢?
问题3小明的父母看到摩天轮转动的方向一致吗?
问题4在实数中,具有相反意义的量是如何表示的?
问题5在旋转形成的角中,如何刻画具有相反意义的角呢?
设计意图问题1为了引出学生熟悉的直角、平角、周角以及720°角,其中720°角已经超出了0°~360°的范围.问题2起着回顾小学、初中角的定义的作用,引导学生从“静态”和“动态”2个角度思考,重点落在本质“转”上,为后续学习作铺垫.问题3帮助学生体会到:考虑旋转所成的角还应考虑方向.通过上述问题可使学生感悟到角的概念有必要做进一步的推广(板书课题).问题4和问题5引导学生类比正、负数,从而将角的概念推广到任意角,即正角、负角和零角.
2 巧设数学问题,合理展开探究
新课程倡导教师开展探究性教学,鼓励学生自主参与学习活动,通过亲身体验,不断质疑,逐步形成勤于动手、乐于探究、努力求知的积极态度.数学的探究性活动,往往是围绕一个实际问题展开.为了能够有效地开展探究性教学活动,本课围绕教学主线,辅助问题链,引导和鼓励学生自主发现问题,自主地探究,设计解决问题的方案,从而自主解决问题.主体教学过程如下:
2.1 巧妙设计教学思路,提炼课堂的教学主线
教学主线:情境→概念→模型→建构→应用→类比理解→拓展.

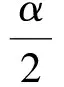
2.2 巧妙利用生活经验,激发学生的参与热情
(1)请学生们说说,生活中还有哪些与角的旋转相关的实例?
(2)以学生们非常熟悉的时钟为研究对象.
问题6若时间慢了25分钟,则校对时间后,分针旋转形成的角为多少?
问题7若时间快了10分钟,则校对时间后,分针旋转形成的角为多少?
问题8若以分针在3点时刻为起始边,旋转90°后,角的终边在什么位置?
问题9在问题8的基础上,再旋转-30°后,角的终边在什么位置?
问题10情境中的直角、平角、周角是象限角吗?
设计意图以学生的生活经验为基础,提出问题,学生的热情一下子被激发起来,答案也多种多样.如:时钟、车轮、音量旋钮、排气扇、剪刀、扳手、体操、跳水等都是旋转形成正、负角很好的例子.时间快慢的校准可以帮助学生进一步强化按逆时针方向旋转形成的是正角,按顺时针方向旋转形成的是负角.另一方面,旋转要确定起始边和终边.为了研究问题的方便,我们引入平面直角坐标系,将角的顶点放在坐标原点,起始边放在x轴正半轴上,从而终边(除顶点外)在哪个象限,就称这个角为第几象限角,终边落在坐标轴上的角称为轴线角.
2.3 巧妙组织课堂活动,提升学生的思维水平
若以时钟的分针为研究对象,分针在3点时刻的位置作为起始边,你能否转出60°角?在60°角的基础上,请转出下列角:420°,780°,1 140°,-300°,-600°.完成下列填空题,并回答相应问题.
420°=60°+______360°,
780°=60°+______360°,
1 140°=60°+______360°,
-300°=60°+______360°,
-600°=60°+______360°.
问题11根据上述经验,与60°角终边相同的角β可以表示为______.
问题12与任意角α终边相同的角β可表示为______.
结论一般地,与角α终边相同的角的集合为β|β=α+k·360°,k∈Z.
设计意图通过学生自己动手实践,边动手、边思考、边归纳,感知420°,780°,1 140°,-300°,-600°角都是与60°角终边相同的角,它们之间相差360°的整数倍.通过设疑来激发学生的思维,让学生体会从具体到抽象、从特殊到一般,逐步归纳得出一般性结论.
2.4 巧妙设计数学例题,培养学生的数学能力
例1写出与下列角终边相同的角的集合,并在0°~360°范围内,找出与之终边相同的角.
(1)650°;(2)-150°;(3)-990°15′.
问题13你能判断上述各角是第几象限角吗?
问题14290°是第几象限的角?
设计意图例1在教材的基础上增加了写出终边相同角的集合的过程,目的是帮助学生快速找到思路,通过问题13强化判断象限角的方法.问题14的目的是引入“形”,从形的角度理解找终边相同的角和判断象限角的方法,即顺时针、逆时针旋转几个整数圈的问题.
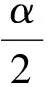
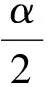
设计意图教材中采用代数方法处理例2,利用代数方法求解,需要分奇数、偶数讨论,学生不易理解.这里可以借助问题引导学生从“形”的角度思考,问题如下:终边相同的角的集合公式中与k相乘的角的度数是“360°”,而这里是“180°”,他们有什么区别和联系呢?学生从形的角度,理解了转一圈和半圈后,问题就迎刃而解了.
思考题(1)终边落在x轴上的角的集合如何表示?
(2)终边落在坐标轴上的角的集合如何表示?
设计意图从正、反2个方面思考问题,进一步加强对图形本质的理解.
3 反思教学内容,提升探究能力
(1)知识结构:

(2)探究方法:类比、归纳、猜想、验证.
(3)拓展探究:请利用互联网搜集与角的概念有关的数学故事,并相互交流.

