立足函数观点观察数列问题——例谈用函数图像性质解决数列问题

●

(天台中学 浙江天台 317200 )

立足函数观点观察数列问题
——例谈用函数图像性质解决数列问题

●陈莹

(天台中学 浙江天台 317200 )

数列内容在高考中占据着非常重要的位置，它对应的试题难度通常在中档或中档以上,尤其在近几年高考卷中，出现了许多与函数紧密相关的数列问题.这些问题是基于函数观点、使用函数思想指导解题的题型,因此，对用函数观点看数列问题的研究有十分重要的意义．

函数思想是中学数学中一种基本的也是主要的数学思想，它应用广泛，但有时应用起来比较困难；它贯穿于整个高中数学．数列是定义域为正整数集N*(或它的有限子集{1,2,3,…,n})的函数，是一类特殊的函数，因此，许多数列问题可以用函数思想、观点和性质来解决.可是人们在解决数列问题时总要遗忘、远离甚至割裂函数知识，因此在教学中加强这一方面的引导是十分必要的．

函数内容的主要构成是概念、性质(定义域、值域及最值、周期性、单调性、奇偶性、对称性)和图像.本文正是基于这样的观点,以例题形式谈论如何解决数列问题．

1 构造函数，利用函数性质解决数列问题

很多数列综合题的解决要紧密联系函数内容，即要经过联想函数、创建函数(模型)、运用函数(有关性质)、解决数列问题等几个阶段.请看下面几个例子．

( )

(2012年四川省数学高考试题)

解f(a1)+f(a2)+…+f(a5)=

2(a1+a2+a3+a4+a5)-(cosa1+cosa2+

cosa3+cosa4+cosa5)=

方法1构造函数，利用函数的单调性.

把a3看成自变量x，构造出函数g(x),令

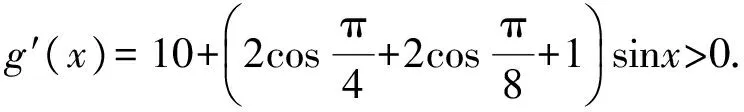
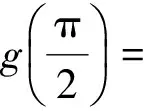
评注本题比较综合，是2012年四川省数学高考选择题的压轴题．上面的解法是本文主题的写真，即站在函数观点的这个高平台上看，数列问题的症结十分清楚，方法得胜出自然．基本程序是通过构造函数

研究其单调性，通过观察找到函数的零点，求出a3的值．这种构造函数利用函数的性质，是解决一些数列综合题的常用方法，但难点是如何发现、构建函数模型．

方法2构造函数，利用函数的对称性.

由f(a1)+f(a2)+…+f(a5)=5π,得

f(a1)-π+f(a2)-π+…+f(a5)-π=0,

构造函数g(x)=2x-cosx-π.因为

g(a1)+g(a2)+…+g(a5)=0，

一定有

即

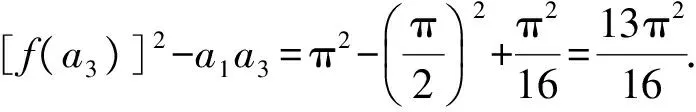
评注这里特别强调的是:在上面有一个“一定有”的推理过程，这个过程不够严格，缺乏依据，跨越太大，作为学生可以用直觉思维判断出来．作为本文，要证明这样的结论，可以考虑证明一个更特殊的命题．

例2已知单调的奇函数y=f(x)，对于项数为k的等差数列{an}，若满足f(a1)+f(a2)+…+f(ak)=0，则一定有a1+a2+…+ak=0．

证明(反证法)不妨设y=f(x)是单调递增的奇函数,若a1+ak≠0，不妨设a1+ak>0，即a1>-ak，一定有

f(a1)>f(-ak)=-f(ak)，

即

f(a1)+f(ak)>0；

再由等差数列{an}的性质，有a2+ak-1>0，同理可得

f(a2)+f(ak-1)>0；

依次类推有

f(a3)+f(ak-2)>0，…，f(ak-1)+f(a2)>0，

f(ak)+f(a1)>0.

把上面的不等式全部同向相加，得

f(a1)+f(a2)+…+f(ak)>0，

与条件矛盾．因此一定有a1+a2+…+ak=0．

以上2种方法都是运用函数的性质圆满解决了问题.本题中通过化简(条件)、凸现(函数模型)是解决问题的第1步，构造函数是解决问题的第2步，也是实质性跨越的一步，难度较大，是学生难以想到的.在教学中，要重视思想方法的落实，促使学生养成这种技能．

2 构造函数，利用函数图像解决数列问题

数与形是中学数学的2条主线，图形起到直观作用，可以启发我们的思维，引出解决问题的办法.要用函数，总是离不开图像,因此，在函数观点下解决数列综合题时，就要经过联想函数、创建函数(模型)、呈现函数(图像)、解决数列问题等过程．

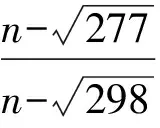
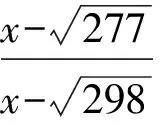
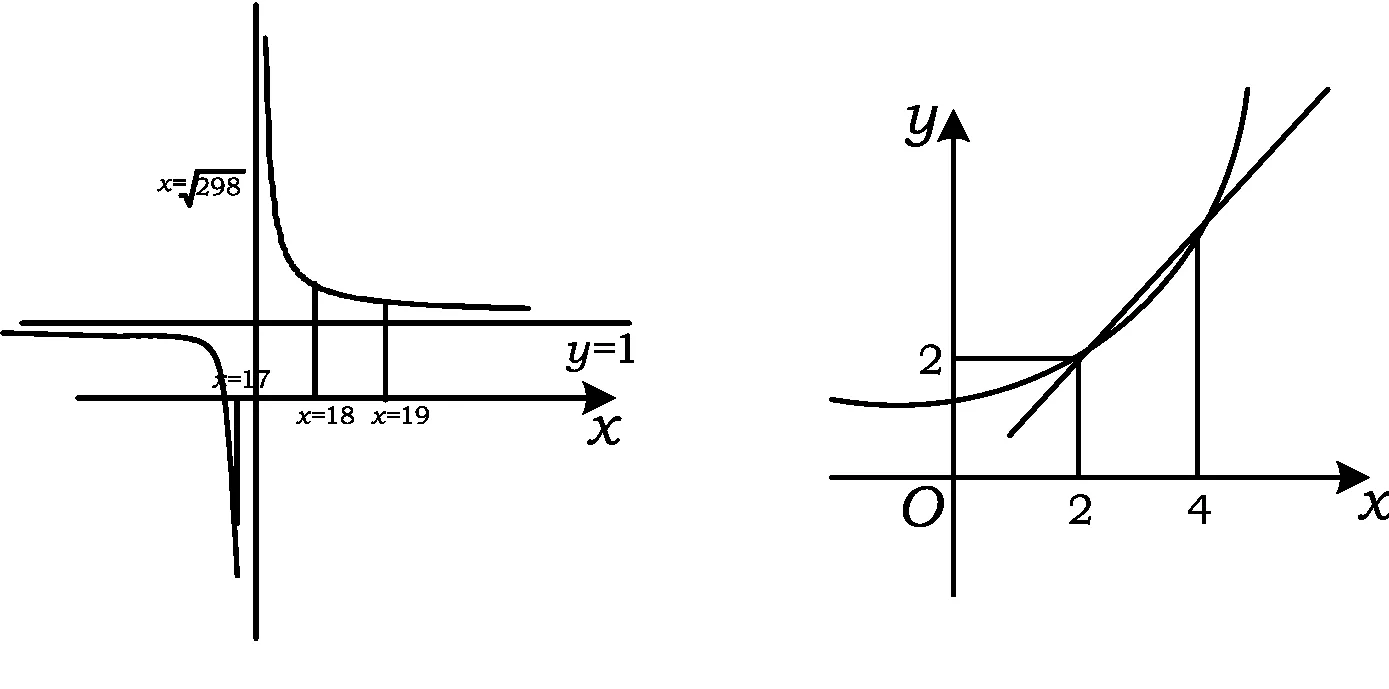
图1 图2

例4已知an是等差数列(公差d≠0)，数列{bn}是等比数列，公比q>1.若a2=b2=2,a4=b4．

(1)比较a1与b1，a5与b5的大小；

(2)猜想并证明an与bn(n≥5)的大小．

分析数列是定义在正整数集合或它的有限子集{1,2,3,4，…，n}上的特殊函数，它是函数概念的继续和延伸，任何数列问题都蕴涵着函数的本质及固有特征．函数图像是函数特征的直观体现，利用图像解决数学问题(以形助数)是解决问题中经常采用的手段．由题意可知an=2+(n-2)d=dn+2-2d，bn=2qn-2,根据函数y=2qx-2(q>1)与y=dx+2-2d的图像可知,在x=2和x=4处有2个公共点，则a1

评注高考中数列题一般都是压轴题，它与不等式、函数、几何等综合在一起．因此函数图像是分析数列中知识常用的工具，有时可为解决问题拓宽思路．

3 例谈几个误区

在教学中，我们经常强调：从函数的观点，数列可以看作是一个定义域为正整数集N*(或它的有限子集{1,2,3,…,n})的函数，因此在解决数列问题时，常用函数的性质去分析.当然如果能将数列与函数有机结合起来，这对解决有关数列问题有很大帮助，能使解题思路更清晰,思维方式更灵活.但数列毕竟有自己的特殊性，与函数有一定的区别，如果不去关注就会导致错误．在教学中，笔者发现学生经常出现以下错误．

3．1 忽视数列具有离散型的特征，一味用函数的单调性解决

例5已知函数

若数列{an}满足an=f(n)(n∈N*)，且{an}是递减数列，则实数a的取值范围是

( )

错解1已知数列{an}是递减数列，由

评注本题中错解原因是把函数的单调性等同数列的增减性，忽视了数列的离散性特征．数列相对函数有自己的特殊性，如果只考虑它是特殊的函数，一味只用函数的增减性来判断和证明就会出错，数列的图像是由孤立的点组成的，数列递减而对应的函数未必单调．在解题中如果牢记这一点，就能减少相关题型的错误．

3.2 忽视数列的定义域

例6数列{an}中，an=-2n2+29n+3，则此数列最大项的值是

( )

(2013年浙江省杭州市高考模拟数学试题)

分析结合二次函数的性质可得

从而当n=7时,an=108为最大值．

评注本题如果不注意数列的定义域是正整数集这一特征，而用二次函数的定义域解题就会出错．

数列问题是数学教学的一大难点，也是高考的重点．通过构造函数及利用函数性质解题，让我们的解题思路更加开阔.学生的认知水平有限,但只要在教学中思想重视，采用一定的方法，注重引导，一定会取得很好的效果．

[1] 褚人统．数形结合对解函数综合题的作用分析[J]．中国数学教育:教师版，2013(1/2)：91-94．

[2] 黄云洁．用函数观点解数列题错解例析[J]．中学数学教学参考，2011(12)：32-33.

[3] 陈云烽．例说数列不等式的证明与探索(续)[J]．中学数学教学参考，2011(12)：25-27.