适性教育下的数学教学
——从日本“一次函数应用”教学案例得到的启示
●
(浙江师范大学教师教育学院 浙江金华 321004)
适性教育下的数学教学
——从日本“一次函数应用”教学案例得到的启示
●刘曌朱哲
(浙江师范大学教师教育学院 浙江金华 321004)
1 问题的提出
适性教育,顾名思义就是适合学生的教育,孔子的“因材施教”可以说是对“适性教育”最好的诠释.数学作为一门具有严谨逻辑思维体系、高度抽象概括性的学科,常常与学生生活经验相脱节,导致多数学生都认为数学枯燥、难学,且无多大用处.如何开展适合学生的数学教育,使学生认为数学有趣且有用,是我国当前数学教育的理论与实践中亟待解决的问题之一.一次函数是学生首次接触的函数,同时它也是初中数学中最基本、重要的内容之一.目前国内不同版本的教科书对一次函数的处理,基本上是通过速度与距离的数量关系、水位的变化或者弹簧的拉伸展开的,与学生生活经验密切相关的内容较少.如何进行适合初中学生的一次函数教学,让学生深入理解一次函数,切身体会它的应用价值,是值得我们研究的.
本文介绍一则来自日本的关于一次函数应用的教学案例,希望提供一个适性教育下开展数学教学的思路,供大家思考.
2 一次函数应用的教学案例
2.1 案例背景

图1 图2
本教学案例[1]主题是一次函数的应用,应用题材为网球发球,即对问题“直线发出的球为了顺利落到对面的发球区,从多少高度发出球最好”的思考.这里忽略球受到的空气阻力及重力影响,即网球所做的是匀速直线运动.运动员从发球线中央(图1中A)发球.图1表示由发球规则所确定的发球区区域大小.为了计算简便,网球场的各部分长度使用图2中的数据.其中,网的高度由地表起算,约为1 m.
2.2 开展教学
2009年12月21日,在日本岐阜県岐阜市立青山中学开展了这次教学,对象为初中二年级学生,共29人.下文是此教学案例的课堂记录,以及笔者对其进行的简单点评.整节课分4个环节有条不紊地进行:第1部分“问题提出——确定课题”;课题确定之后,学生通过资料卡的学习进行“课题探索”;待所有学生均将问题解决之后,进行第3部分“意见交流、总结”;在全体学生、教师进行交流的基础上,教师针对此次教学进行了“及时反馈”,以了解学生是否达到预定的学习目标.
2.2.1 问题提出——确定课题
教师播放网球视频.视频有2种:一种是尽全力打出直线球,却没有进入对面发球区;另外一种是松弛地自由发球,使网球像小山一样的弧线进入对面发球区.首先播放第一个视频,引导学生思考为什么第一个动画中全力发出的直线球没有进入发球区.学生进行了各种猜测.
T:为什么球没有进入发球区呢?
S1:可能还需要多加练习吧.
S2:发球力量不够吧.
点评题材选取的合适与否,直接决定了课堂教学的成败.这里教师由学生生活经验出发,以网球这一日本学生非常熟悉且热爱的运动为切入点,在一开始就吸引了学生的注意力,对于接下来要发生什么学生都满怀期待,为接下来的课题探索作好了精神准备.积极调用学生的生活经验进行教学,提高了教学效率,并且使学生对教学内容产生积极共鸣与浓厚兴趣.
此时,播放第2个视频,学生似乎明白了改变击球方式可以使球顺利进入对面发球区.紧接着再重新播放第一个直线击球的视频.
T:假设将击球高度设置在2.4 m高处,全力击球,球会进入发球区吗?
(学生陷入思考当中.)
S部分:可以进去.
S部分:不能进去.
点评引导学生进行思考并产生要解决的问题,是数学课堂中至关重要的一点.教师在这里成功地将学生引入了思考当中,为接下来的问题解决做好了铺垫.
学生开始议论纷纷,表现出感兴趣的样子.此时,这节课的课题已经渐渐明晰.如图3中的位置发球,与网的上端连接成一条直线.根据以上假设,考虑:
问题1直线发出的球为了顺利落到对面的发球区,从多高的高度发出球最好(图3)?
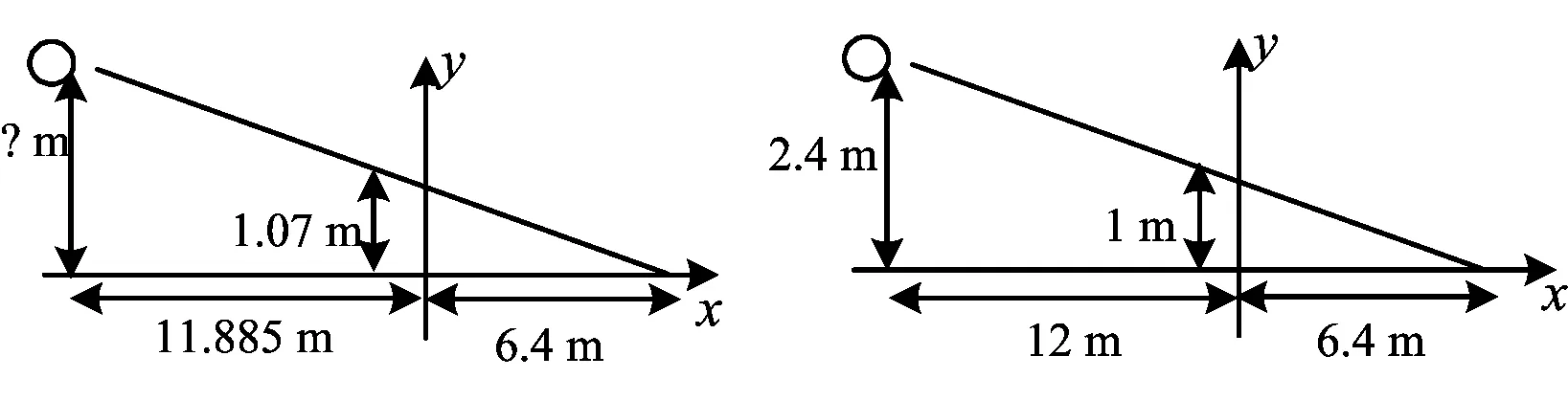
图3 图4
问题2从2.4 m高度直线发出的球能否顺利落到对面的发球区(图4)?
接着,教师和学生一起确定了全力击出球的轨迹是一条直线.
T:大家思考一下是否可以用我们所学过的数学知识表示直线呢?
S全体:一次函数.
然后,教师引导全体学生选取合适的坐标轴,坐标轴的选取是本次授课的难点.在教师和学生的共同讨论下,选取地面为x轴,网球场中央网所在直线为y轴.由此,确定了此次教学的课题.
点评在“问题提出——确定课题”这一部分,教师以问题为导向,将学生自然而然地带入了网球发球的问题情景中.从学生经验出发,抛出了学生感兴趣的问题,由此激发了学生的内在学习动机,使学生自己有兴趣和想法,并且想要去探索并解决这个问题.这一点值得我们学习.
2.2.2 课题探索
确定课题之后,教师引导学生自主完成问题的探索求解.这里提供学生研究的学习资料卡分为2种:资料1和资料2.
资料1供数学学习中等以上的学生.资料中仅给出问题求解所需的数据,以及2个需要探讨、研究的问题,希望学生能通过研究使问题得到解决.
高度!几米?
2年级______组 姓名______
问题:考虑尽全力打出的直线球.
课题:从2.4 m高度直线发出的球能否顺利落到对面的发球区?考虑用一次函数解决.

图5 图6
评价问题:直线发出的球为了顺利落到对面的发球区,从多高的高度发出球最好?
资料2供数学学习稍有困难的学生,其中设置了多个提示项,引导学生一步步解决问题.从一次函数解析式的分步求解,到将已求解的数学问题转化为实际问题的应用,每一步都有相应提示,保证学习困难的学生也可以顺利完成课题.
高度!几米?<提示卡>
2年级______组 姓名______
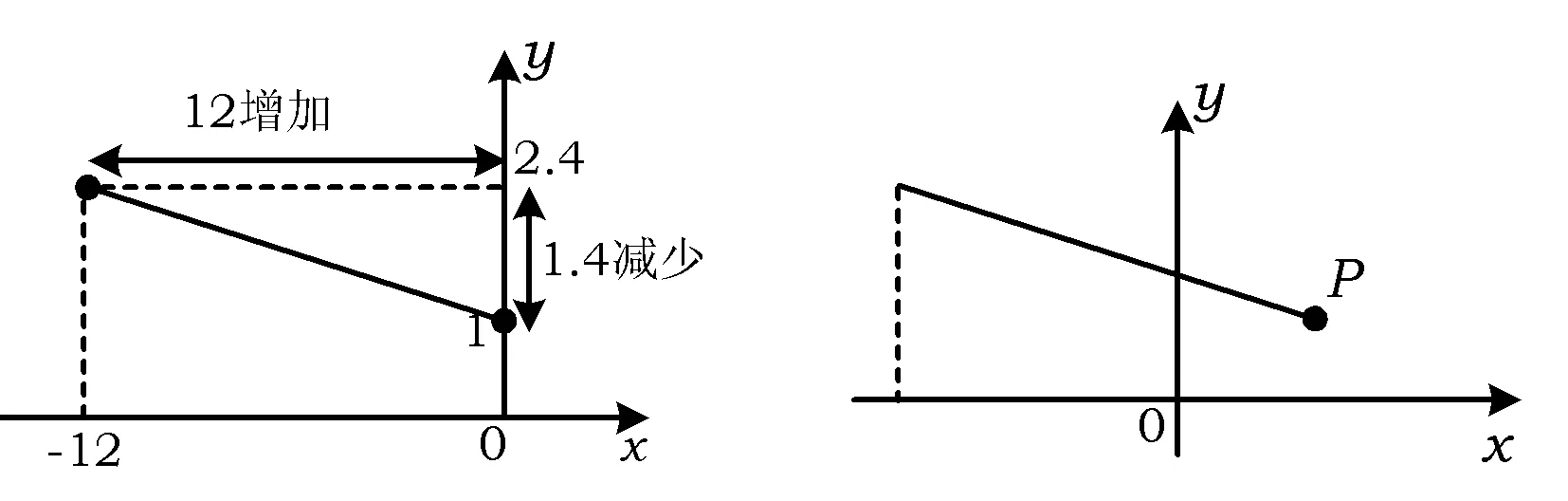
图7 图8
图7中的点表示通过一次函数直线上的2个点:(0,1),(-12,24),与y轴交点的截距是______.
由此可得出一次函数的解析式为:y=______.
如图8,假如知道点P的坐标,那么就可以知道中央网到网球所落点的距离.
点P的纵坐标为0,将0带入一次函数y=______中……可得点P坐标为______.
由此可得出中央网到网球所落点的距离为______m.
从中央网到发球线末端的距离约为6.4 m,那么高2.4 m击出的球……
学生在进行探索时,教师同时进行教学观察.如果拿到资料1的学生感到有困难,教师就将资料2发放给学生,让其继续探索.对遇到还有困难的学生进行必要的提示和帮助,把握所有学生探索研究的进展过程.
点评至此可以看出,教师所采用的是自主探究的学习方式.此处的亮点是教师分发给学生的学习资料卡是有针对性.资料1与资料2分别兼顾了学有余力和学有困难的学生,充分体现了因材施教的观点.第2个值得我们关注的是教师对动态课堂的掌控,对预设教学与生成教学之间的平衡把握.教师在学生进行课题探索的同时,对学生进行观察,及时发现学生学习中遇到的困难,并进行必要的教学策略调整,这样就把握了课堂向高效的方向发展.真实的课堂总是会发生这样那样的情况,教师要通过观察、对话、交流等方式,关注学生如何学习、会不会学习以及学习的程度等等,及时帮助学生改善学习行为,提高课堂效率.
2.2.3 意见交流、总结
每个学生根据自己探索的结果,就“直线发球是否可以进入对面的发球区吗”进行交流讨论.教师指定2名学生(分别是学习优良生和学习有困难学生)对自己的方法进行板演.
S1:求出直线的斜率,知道直线上一点的坐标,带入直线的一般式y=ax+b.
S2:由一次函数变化量总是相等这一性质出发,导出结论.
全班学生一起进行了激烈的讨论,判断哪一种方法可以求出网球是否能落入发球区.
教师继续引导大家:还有别的方法可以判断吗?
最后29个学生一致认为在所给出的条件下,网球是无法进入发球区的.
点评注意到“每个同学……进行交流讨论”、“29个学生一致认为……”、“全班学生一起进行了激烈的讨论”,教师关注到了每个学生对课题的见解,让学生充分展示自己的个人思想,让每一位学生参与问题解决.课堂是教师的,也是学生的,教师作为课堂的一份子,与学生共同完成课题的探索.这里不存在纯粹的教师与学生,而是一群作为教师的学生和一个作为学生的教师.
2.2.4 及时反馈
T:通过本节课的学习,大家都学到了什么?
S:一次函数、变化率、读图与作图、阅读、代入法、正数、负数.
T:除了网球的发球以外,你们认为一次函数还可以应用在哪些类似的场合?
S:棒球的投手进行击球的时候、足球、羽毛球、排球、乒乓球、篮球.
T:再回顾一下今天的内容,大家有什么收获?
S1:知道了从2.4 m的高度击出的球是否能落入发球区,感到很高兴.
S2:原来运动场上的问题也可以用数学求解呀!
S3:网球的发球竟然可以用一次函数来思考,感觉好神奇!
S4:原来一次函数还可以表示我们身边发生的事物,感到好惊讶呀!
S5:我想调查一下身边还有哪些问题可以使用一次函数解决.
S6:一次函数原来是有用的啊!
S7:今天之前,我一直认为一次函数是没有用的,而且觉得也很难.今天了解到一次函数竟然可以应用到身边的场景.
……
点评及时反馈可以帮助教师确定学生是否达到了预定学习目标.这一部分教师分别从知识与技能、过程与方法、情感态度这3个方面进行反馈提问,可以看出原本觉得数学没有多大乐趣和用处的学生们对数学有了重新的认识,并且知识与技能方面也得到了巩固.而且可以看出,教师在进行适当引导后,学生可以将所学知识迅速迁移到类似的场景中进行应用.
3 结论与启示
以上的教学案例,让数学课堂有了耳目一新的感觉,教师的“教”是为了学生的“学”,学生的“学”带动了整个课堂的学习氛围.从这则一次函数应用的教学案例可以看出,日本的课堂最显著的一个特点就是“以学习为中心的教学”,关注每一位学生的成长,实现每一位学生真正的学习.不仅关注“上层”学生的学习,也关照到了“下层”学生的学习,同时,通过教学观察,及时调整策略,使所有的学生都能在原有的经验基础上实现有意义的学习.
综合来看,这则教学案例有以下一些特点:(1)从学生经验出发,精心组织教学,通过情景导入吸引学生注意;(2)兼顾每位学生的学习发展,注重因材施教的教学思想;(3)以问题解决贯穿整个课堂教学始终.让学生通过问题解决的过程学习数学,通过具有实际意义的问题解决帮助学生充分认识数学的应用价值和树立正确的数学观;(4)在教师的组织下,学生充分发表自己的见解,并且与学生进行探讨,最终获得对问题的一致性认识.
适性教育下的数学教学该如何开展,怎样的数学课堂才是适合学生的?从这则来自日本的教学案例,我们可以得到一些启发.笔者认为以下3点是可以借鉴学习的.
3.1 关注学生的生活经验,激发内在学习动力
数学是一门高度抽象与概括的学科,对于大部分学生而言,数学中很多内容本身就是枯燥、难懂、没有任何乐趣的,甚至在短期看来是毫无用处的.如何构建适合学生的数学课堂,使学生想要学习且乐于学习数学是教学必须关注的重要问题.关注学生的生活经验是一个很好的途径.由这则教学案例可以看出,教师选取的是日本学生所熟悉且热爱的网球为素材,在课堂开始就吸引了学生的注意,从问题的探索求解,到之后师生之间的交流,都可以看出学生充满了兴趣,对课题的探索也是源于内心的真实情感,学生的内在学习动机也有效地促进了课题的探索,由此才有了这次课堂的成功.我们的数学教学也应以学生的生活经验为基础,从学生熟悉、热爱的场景出发,吸引学生的注意,激发学生的内在的学习动机.我们知道,当学生的学习是以内部动机为主时,他是真正对学习产生了兴趣,是对学习活动的热爱,能更为有效地进行和坚持学习活动[2].如此一来,学生有兴趣学了,也能学好了,并且在问题解决的过程中也树立了正确的数学观,认识到了数学的应用价值.
3.2 注重学生的个体差异,兼顾课堂公平
认知心理学认为,即使处于同一年龄时期的儿童,在智力发展水平、认知风格、兴趣等方面都存在着明显的个体差异.学生在进行数学学习时,其认知水平、起点状态、情感态度也不同程度地存在着差异,这就必然要求为他们提供适合其状态的教学.因此必须敢于承认学生的差异,敢于根据学生差异而教,敢于教出“差异”来,而不能按照一个标准搞“一刀切”[3].这里“课题探索”部分教师在引导学生自主学习的同时,充分关注了学生的学习起点状态、学习能力差异等,并有针对地准备了2种学习资料卡,因材施教的同时,也保护了每位学生的学习自尊心,树立了学习自信心.因此,适合学生的数学教学应该是立足学生差异,关注学生的学习起点水平、学习能力与情感态度,并在此基础上进行针对性的教学,满足每一个学生的学习需要,使所有的学生都能在原有基础上得到充分的发展.
与此同时,关注学生的个体差异在一定程度上体现了教育公平.在我国长期的数学教育实践中,往往可以看到教师对学业成绩优良和学业成绩不良的学生采用的都是统一的教学内容与进度、统一的教学方法和统一的评价方式,这样就导致了强者更强、弱者更弱的两极分化的极端现象,学困生往往也是这样产生的.这种忽略学生差异的教学其实就是教育不公平的一种体现.
3.3 构建和谐宽松的课堂氛围,创建学习共同体
佐藤学教授说:“学校和教师的责任并不在于‘上好课’.学校和教师的责任乃在于:保障每一位学生的学习权,提供学生挑战高水准学习的机会”[4].数学课堂更是如此,原来“填鸭式”、“满堂灌”的时代早该进入博物馆了.从这例日本课堂可以看出,教师与学生是亲密的伙伴关系,没有出现教师独挡一面、学生侧耳倾听的现象.教师在课堂上最主要的任务是促成每一位学生真正意义上的学习,使每一位学生都能有所进步.学生也在师生、生生间的共同交流中丰富了知识,扩展了思维.课堂就应该是这样,是每位学生与教师共同学习进步的一个平台.因此,数学教师的责任不在于“上好课”,更重要的是作为引导者、合作者、伙伴,与学生共同构建合作学习、互帮互助、共同进步的课堂.这样的课堂才能提供给每一位学生学习的机会与权力,才有可能实现每一位学生真正意义上的学习.“教是为了不教,学是为了会学”,数学课堂不应该单纯是教师讲授的平台,更应该是学生共同学习、共同进步的平台.
(注:本文系2011年度浙江省教育厅科研项目“初中‘适性教育’的理论与实践”(编号:Y201122231)的研究成果之一.)
[1] 後藤弘樹,愛木豊彦.テニスのサーブを題材とする1次関数の活用[J].岐阜数学教育研究,2010(9):62-69.
[2] 陈琦,刘儒德.教育心理学[M].北京:高等教育出版社,2010:194.
[3] 姜智,华国栋.“差异教学”实质刍议[J].中国教育学刊,2004(4):52-55.
[4] 佐藤学.学校的挑战:创建学习共同体[M].钟启泉,译.上海:华东师范大学出版社,2010:1-2.

