半无限周期光子晶体全反射隧穿机理的干涉诠释

刘启能

(重庆工商大学计算机科学与信息工程学院，重庆400067)

1 引言

所谓光子晶体就是其介质的折射率在空间上呈周期性变化的带隙材料，当光在光子晶体中传播时由于光子晶体的周期结构会产生光的带隙。利用光的带隙结构可以十分方便地控制光的传播，这使得光子晶体成为控制光传播的理想材料。根据其周期结构的空间维数不同光子晶体分为一维光子晶体、二维光子晶体和三维光子晶体。一维光子晶体的结构最简单、研究最方便，但是它却具有其他高维光子晶体的基本特性。因此对一维光子晶体的研究成为光子晶体研究领域内的重要内容。

光子晶体的研究中，在带隙特性［1－5］、缺陷模特性［6－9］、滤波理论［10－11］等方面已经取得了可喜成果。近年来人们又发现了光以大于全反射角入射一维光子晶体时出现的全反射隧穿现象［12］。随后文献［13］中利用传输矩阵法研究了TE波和TM波两种偏振光以大于全反射角入射一维光子晶体时出现的全反射隧穿现象，得出了TE波和TM波在一维光子晶体的全反射隧穿现象随入射角和结构参数的变化特征。接着文献［14］利用传输矩阵法进一步研究了一维光子晶体的全反射隧穿效应的滤波特性，发现一维光子晶体的全反射隧穿效应比一维掺杂光子晶体具有更好的梳状滤波特性。为了解释一维有限周期光子晶体的全反射隧穿效应产生的物理机理，文献［15］利用多光束干涉理论推导出一维有限周期光子晶体的全反射隧穿导带频率中心满足的解析公式，从理论上解释了一维有限周期光子晶体的全反射隧穿效应产生的物理机理。随后文献［16］通过建立一维半无限周期光子晶体的谐振腔模型，利用谐振腔的共振条件推导出全反射隧穿导带波长满足的解析公式，建立了一维半无限周期光子晶体全反射隧穿效应的共振理论。从理论上解释了一维半无限周期光子晶体的全反射隧穿效应产生的物理机理。并将共振理论的结果与色散法的结果进行比较，其结果完全吻合。但是文献［16］中存在一个明显的不足:它只得出了一维半无限周期光子晶体的全反射隧穿导带波长的解析公式，而全反射隧穿峰的峰高和带宽两个重要特征没有得到给予解决。因此，文献［16］中的共振理论是一个不完善的理论，有待进一步深入研究和完善。本文在文献［16］的基础上，利用光的干涉理论推导出一维半无限周期光子晶体的全反射隧穿峰的透射率公式和波长公式，解释一维半无限周期光子晶体的全反射隧穿现象的产生机理，对全反射隧穿峰的波长中心、峰高、带宽进行全貌研究。

2 隧穿现象

仍用文献［16］中的一维半无限周期光子晶体结构，它由氟化镁(其厚度为 d1、折射率为 n1=1.38)和碲化铅(其厚度为d2、折射率为n2=4.1)两种介质周期性地交替构成，其周期为无限多个。如图1。设入射空间的介质也为碲化铅，即n2=n0。因n0＞n1，所以当光大于全反射角入射该一维半无限周期光子晶体时会产生全反射现象，其全反射角θm=arcsinn1/n0=0.34rad。取中心波 长 λ0=600nm，设归一化波长Λ=λ/λ0，λ为光在真空中的波长。

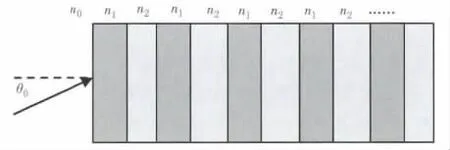
图1 一维半无限周期光子晶体Fig.1 1D half infinite cycle photonic crystal

取n1d1=n2d2=λ0/4、θ0=0.35rad，计算出TE 波入射该光子晶体其色散函数F［17］随归一化波长Λ的响应曲线，如图2。由图2可知，当光大于全反射角入射一维半无限周期光子晶体时会出现全反射隧穿现象。其全反射隧穿现象具有以下特征:全反射隧穿现象是由多级导带组成，波长最大的隧穿导带称为一级隧穿导带，随作波长的减小分别称为二级隧穿导带、三级隧穿导带、……。图2中归一化波长Λ在0.45附近的是一级全反射隧穿导带，归一化波长Λ在0.23附近的是二级全反射隧穿导带，…。各级全反射隧穿导带的带宽随级数的增加而减小。

图2 色散函数随归一化波长响应曲线(θ0=0.35rad)Fig.2 Response curves of dispersion function versus wavelength

图3 多波束干涉模型Fig.3 multiple-beam interference model

图4 透射率随归一化波长响应曲线(干涉理论)Fig.4 Response curves of transmissivity versus wavelength

3 干涉理论

为了解释一维半无限周期光子晶体全反射隧穿现象的产生机理，建立一维半无限周期光子晶体的多光束干涉模型:当光以大于全反射角入射该光子晶体时，由于n0＞n1，光会在从n0入射到n1的界面上发生全反射，但光并不是完全不能进入n1中，它能够以倏逝波的形式进入n1约一个波长的深度。而该光子晶体中n1层的厚度d1约为0.2个波长，因此光能够穿过n1层进入n2层中。当光进入n2层后，会在n2层的前后两个平行界面间往复地反射形成一个谐振腔，如图3。该一维半无限周期光子晶体就由无限多个这样的谐振腔连续排列组成。当光在n2层中第一次反射时会产生透射光线1、第二次反射时会产生透射光线2、第三次反射时会产生透射光线3、……，这些无限多条透射光线会发生相干干涉，其相干干涉出现极大的位置就会产生全反射隧穿现象。由多光束干涉理论［18］可得，这无限多条透射波线发生相干干涉的透射率为:

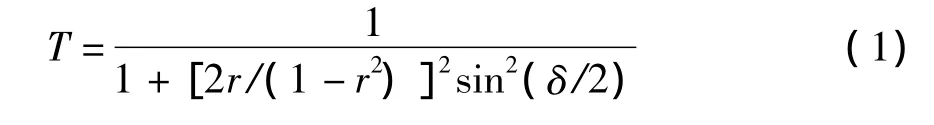
式中，r为n1，n2两层界面的反射系数，δ为相邻两条透射光线的位相差，δ为:

式中，θ2，λ2分别为n2层中光的折射角和波长。由数学知识可知，要使式(1)出现极大值必须满足下列条件:

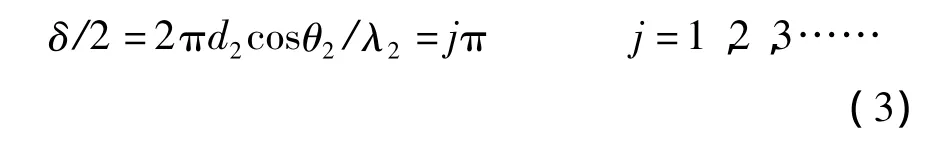
式(3)就是出现一维半无限周期光子晶体全反射隧穿现象的条件。利用θ2=θ0和λ2=λ/n2，由式(1)得出全反射隧穿峰的透射率随归一化波长Λ和入射角θ0的变化关系:

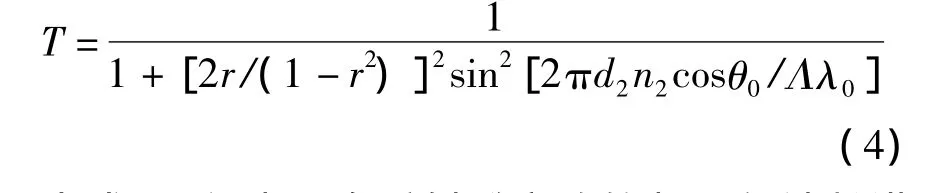
由式(3)得出现全反射隧穿峰的归一化波长满足的条件为:

式中，j称为全反射隧穿峰的级数，j=1对应一级全反射隧穿峰，其归一化波长为Λ1，j=2对应二级全反射隧穿峰，其归一化波长为Λ2，……。取n2d2=λ0/4、θ0=0.35 rad，由式(4)计算出全反射隧穿峰的透射率随归一化波长的响应曲线，如图4。由图4可以看出:在归一化波长 Λ=0.45、0.24、0.15……附近分别出现了一级隧穿峰、二级隧穿峰、三级隧穿峰……，各级全反射隧穿导带的带宽随级数的增加而减小，干涉理论的结果与色散法的结果吻合。这表明干涉理论能成功地解释一维半无限周期光子晶体全反射隧穿现象的产生机理。

还可以发现:式(5)与文献［16］中用共振理论推导出的全反射隧穿导带的归一化波长公式完全相同。而上述全反射隧穿的干涉理论与文献［16］中的共振理论是建立在不同的理论基础上的，两种不同的方法能够得出相同的结论，这表明干涉理论和共振理论都是解释一维半无限周期光子晶体全反射隧穿现象的正确理论。并且干涉理论中的公式(4)不仅能够得出全反射隧穿峰的归一化波长公式(5)，而且还能反映全反射隧穿峰高、宽度等信息。因此，本文建立的全反射隧穿的干涉理论比文献［16］建立的全反射隧穿的共振理论更加全面地、深刻地揭示了产生一维半无限周期光子晶体全反射隧穿现象的物理机理。

4 全反射隧穿峰的特征分析

为了进一步比较干涉理论与共振理论，下面利用干涉理论(即式(4))和共振理论(即式(5))对全反射隧穿峰的特征进行比较研究。

4.1 隧穿峰随入射角的变化

取n2d2=λ0/4，利用式(4)计算出一级全反射隧穿峰随归一化波长和入射角变化的3D图，如图5。利用式(5)计算出一级全反射隧穿峰的归一化波长随入射角的响应曲线，如图6。

图5 隧穿峰随波长和入射角变化3D图(干涉理论)Fig.5 Response curves of tunneling peak versus wavelength and incident angle

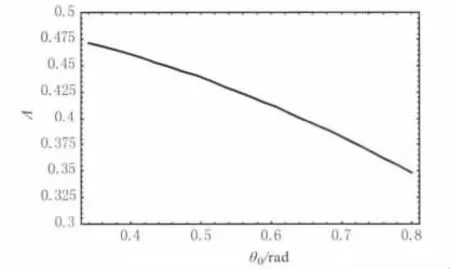
图6 隧穿峰波长随入射角响应曲线(共振理论)Fig.6 Response curves of wavelength versus incident angle

比较图5和图6可以得出:

①一级全反射隧穿峰的归一化波长随入射角的增加而减小，干涉理论与共振理论得出完全相同的结果。

②但图6中的共振理论的图像只能反映全反射隧穿峰的归一化波长随入射角的变化特征，却不能反映全反射隧穿峰的峰值和带宽随入射角的变化特征。而图5中的干涉理论的图像却能够反映全反射隧穿峰的峰值和带宽随入射角的变化特征。

4.2 隧穿峰随腔厚度的变化

腔厚度就是的d2，为了研究方便令d2=Xλ0，X为无量纲的参变量，腔厚度的变化通过X的变化实现。式(4)和式(5)可以化为随X的变化函数:

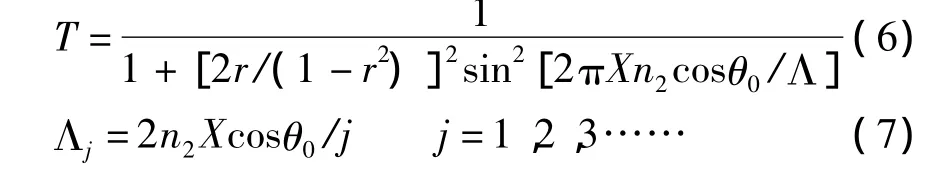
固定θ0=0.35 rad，利用式(6)计算出一级全反射隧穿峰随归一化波长和腔厚度变化的3D图，如图7。利用式(7)计算出一级全反射隧穿峰的归一化波长随腔厚度的响应曲线，如图8。比较图7和图8可以得出:

①一级全反射隧穿峰的归一化波长随腔厚度的增加而成正比增加，干涉理论与共振理论得出完全相同的结果。

②但图8中的共振理论的图像只能反映全反射隧穿峰的归一化波长随腔厚度的变化特征，却不能反映全反射隧穿峰的峰值和带宽随腔厚度的变化特征。而图7中的干涉理论的图像却能够反映全反射隧穿峰的峰值和带宽随腔厚度的变化特征。

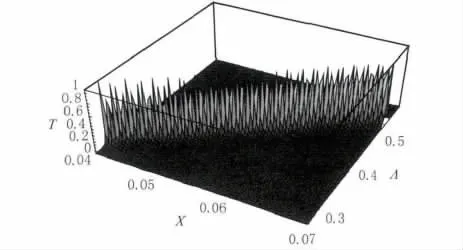
图7 隧穿峰随波长和腔厚度变化3D图(干涉理论)Fig.7 Response curves of tunneling peak versus wavelength andX

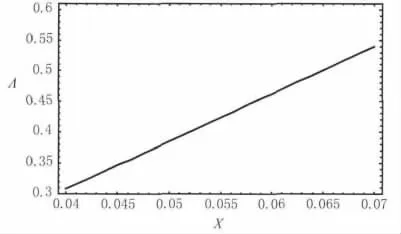
图8 隧穿峰波长随腔厚度响应曲线(共振理论)Fig.8 Response curves of wavelength versus X

5 结论

前面通过建立一维半无限周期光子晶体的多光束干涉模型，利用光的干涉理论推导出一维半无限周期光子晶体全反射隧穿峰的透射率公式和波长公式。利用透射率公式和波长公式成功地解释了一维半无限周期光子晶体全反射隧穿现象产生的物理机理，并利用干涉理论和共振理论对一维半无限周期光子晶体全反射隧穿现象的特征进行了比较研究，两者的结论是一致的。干涉理论不仅弥补了色散法不能解释全反射隧穿现象产生机理的不足，而且弥补了共振理论不能反映全反射隧穿峰的峰值和带宽的不足。

［1］ Wang Rui，Zhang Cunxi，Nie Yihang.Band structure and propagation properties of one-dimension anisotropy photonic crystalsl［J］.Acta Photnica Sinica，2007，35(1):89 －92.(in Chinese)王瑞，张存喜，聂一行.一维各向异性光子晶体的带隙结构和传输特性［J］.光子学报，2007，35(1):89 －92.

［2］ Li Rong，Ren Kun，Ren Xiaobin.Angular and wavelength selectivity of band gaps of holographic photonic crystals for different polarizations［J］.Acta Phys.Sin.2004，53(08):2520 －2523.(in Chinese)李蓉，任坤，任晓斌.一维光子晶体带隙结构对不同偏振态的角度和波长响应［J］.物理学报，2004，53(08):2520－2523.

［3］ Liu Qineng.Transmission characteristics of electromagnetic wave in 1D rectangle photonic crystal［J］.Acta Photnica Sinica，2010，39(5):847 －850.(in Chinese)刘启能.一维矩形光子晶体中电磁波的传输特性［J］.光子学报，2010，39(5):847 －850.

［4］ Zhang Gaoming，Peng Jingcui，Jian Zhijian，et al.Orthogonality relations among modes in left-handed materials slab waveguide［J］.Acta Physica Sinica，2006，55(4):1846 －1849.(in Chinese)张高明，彭景翠，翦知渐，等.左手材料薄板波导中模式之间的正交关系［J］.物理学报，2006，55(4):1846－1849.

［5］ Xu Xuming，Fang Liguang，Liu Nianhua.Unusual photonic tunneling in multilayer system with a negative refraction Index layer［J］.Acta Optica Sinica，2005，25(12):1676 －1679.(in Chinese)徐旭明，方利广，刘念华.含负折射率层的多层体系的反常光子隧穿［J］.光学学报，2005，25(12):1676－1679.

［6］ Liu Qineng.Effect of impurity absorption on one-dimen-sional photonic crystal defect mode［J］.Chinese Journal of Lasers，2007，34(6):777 －780.(in Chinese)刘启能.杂质吸收对一维光子晶体缺陷模的影响［J］.中国激光，2007，34(6):777 －780.

［7］ Shang Tingyi，Zheng Yi，Zhang Huiyun.Omnidirectional gap and defect mode of one-dimensional photonic crystals with negative-index materials［J］.Acta Photonica Sinica，2007，36(4)663 －666.(in Chinese)尚廷义，郑义，张会云.含负折射率材料一维光子晶体的全方位带隙和缺陷模［J］.光子学报，2007，36(4):663－666.

［8］ Liu Qineng.The mode and defect mode of electromagnetic wave in rectangular doped photonic crystal［J］.Acta Physica Sinica，2010，59(4):2551 －2555.(in Chinese)刘启能.矩形掺杂光子晶体中电磁波的模式和缺陷模［J］.物理学报，2010，59(4):2551 －2555.

［9］ Liu Qineng.The defect mode and the quantum effect of light wave in cylindrical anisotropic photonic crystal［J］.Acta Physica Sinica，2011，60(1):0142171 － 0142174.(in Chinese)刘启能.各向异性圆柱掺杂光子晶体的缺陷模及其量子效应［J］.物理学报，2011，60(1):0142171 －0142174.

［10］ Liu Qineng.Filtering feature of 1D rectangle doping photonic crystal［J］.Chinese Journal of Lasers，2010，37(8):2041 －2044.(in Chinese)刘启能.一维矩形掺杂光子晶体的滤波特性［J］.中国激光，2010，37(8):2041 －2044.

［11］ Li Wensheng，Zhang Qin，Huang Haiming，et al.Frequency-multiplication filter based on photonic crystal［J］.Journal of Synthetic Crystals，2012，41(4):1125 － 1129.(in Chinese)李文胜，张琴，黄海铭，等.一种基于光子晶体的多通道倍频滤波器［J］.人工晶体学报，2012，41(4):1125－1129.

［12］ Fang Yuntuan，Liang Zhongcheng.Unusual transmission through usual one-dimensional photonic crystal in the presence of evanescent wave［J］.Opt Commun，2010，283:2102－2106.

［13］ Liu Qineng.Total reflection through effect of light in 1D photonic crystal［J］.Acta Photnica Sinica，2011，40(2)232 －235.(in Chinese)刘启能.光在一维光子晶体中的全反射贯穿效应［J］.光子学报，2011，40(2):232 －235.

［14］ Liu Qineng.Theoretic study of total reflection through effect polarization filter of photonic crystal［J］.High Power Laser and Particle Beams，2011，23(4):1091 － 1094.(in Chinese)刘启能.光子晶体全反射贯穿偏振滤波器的理论研究［J］.强激光与粒子束，2011，23(4):1091 －1094.

［15］ Liu Qineng.Analytical study on total reflection tunnel effect of 1 － D photonic crystal［J］.Acta Optica Sinica，2012，32(2):0219002.(in Chinese)刘启能.一维光子晶体的全反射隧穿效应的解析研究［J］.光学学报，2012，32(2):0219002.

［16］ Liu Qineng.Resonance theory of the total reflection tunnel effect of half infinite period photonic crystal［J］.Acta Photnica Sinica，2012，41(8):986 －989.(in Chinese)刘启能.半无限周期光子晶体全反射隧穿效应的共振机理［J］.光子学报，2012，41(8):986 －989.

［17］ Liu Qineng.New dispersive method of stratified medium and its application in photonic crystal［J］.Laser ＆ Infrared，2009，39(6):643 －646.(in Chinese)刘启能.分层介质的新色散法及其在光子晶体中的应用［J］.激光与红外，2009，39(6):643 －646.

［18］ E Hecht，A Zajac.Optics［M］.Beijing:People’s Education Press，1980:691 －693.(in Chinese)E赫克特，A赞斯.光学［M］.北京:人民教育出版社，1980:691－693.