展开法求解变系数KP方程的精确解*

郭冠平

(浙江师范大学 教师教育学院,浙江 金华 321004)

郭冠平

(浙江师范大学 教师教育学院,浙江 金华 321004)

0 引 言

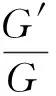
的解.可以看出,这种方法直接且有一般性，适合于处理这类非线性演化方程.

1 变系数KP方程的精确解

对于方程(1)，设

并设式(1)有如下的解:

式(3)中,G=G(ξ)满足如下二阶线性常微分方程(LODE)：

式(4)中,Ai(i=0,1,…,n),λ,μ是待定的常数；n由齐次平衡法(平衡最高阶导数项和非线性项)确定.

由齐次平衡法可知，n=2，所以式(3)变为

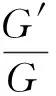
以上各式中,ρ=120f2A2ξ4x+60f1A22ξ2x.

从式(6)中可以求得

(15)

把式(13)～式(15)代入式(5)，得

当λ2-4μ>0,λ2-4μ<0,λ2-4μ=0时，分别可以得到双曲函数形式解、三角函数形式解和有理函数形式解.限于篇幅，本文只讨论λ2-4μ>0的情况,其中:

把式(17)代入式(16)，可得式(1)的新精确解.其中C1,C2是任意常数.

(18)

特别地，取C1=0,C2≠0时,得到孤波解为

特别地，取C2=0,C1≠0时,得到孤波解为

若取ξ=kx+by+ct+ξ0,其中:k,b,c,ξ0为任意常数，则式(18)～式(20)分别变为行波解

(23)

2 结 语

[1]Wang Mingliang.The solitary wave solutions for the variant Boussinesq equations[J].Physics Letters A,1995,199(3/4):169-172.

[2]张解放.长水波近似方程的多孤子解[J].物理学报,1998,47(9):1416-1420.

[3]范恩贵,张鸿庆.非线性孤子方程的齐次平衡法[J].物理学报,1998,47(3):353-361.

[4]王明亮,李志斌,周宇斌.齐次平衡原则及其应用[J].兰州大学学报:自然科学版,1999,35(3):8-16.

[5]郑贇，张鸿庆.一个非线性方程的显式行波解[J].物理学报,2000,49(3):389-391.

[6]闫振亚,张鸿庆,范恩贵.一类非线性演化方程新的显式行波解[J].物理学报,1999,48(1):1-5.

[7]张桂戍,李志斌,段一士.非线性方程的精确孤立波解[J].中国科学:A辑 数学,2000,30(12):1103-1108.

[8]郭冠平,张解放.关于双曲函数方法求孤波解的注记[J].物理学报,2002,51(6):1159-1162.

[9]郭冠平,张解放.长短波相互作用方程的Jacobi椭圆函数求解[J].物理学报,2003,52(11):2660-2663.

[10]郭冠平,张解放.非可积(3+1)维KdV型方程的一类多孤子解[J].西安石油学院学报,2002,17(3):82-84.

[11]刘式适,傅遵涛,刘式达,等.Jacobi椭圆函数展开法及其在求解非线性波动方程中的应用[J].物理学报,2001,50(11):2068-2073.

[12]套格图桑，白玉梅.构造非线性发展方程无穷序列类孤子精确解的一种方法[J].物理学报,2012,61(13):130202.

[13]李帮庆,马玉兰.(G′/G)展开法和(2+1)维非对称Nizhnik-Novikov-Veselov系统的新精确解[J].物理学报,2009,58(7):4373-4378.

[14]Zhu Zuonong.Painlevé property,Bäcklund transformation,Lax pair and soliton-like solution for a varianble coefficient KP equation[J].Physics Letters A，1993，182(2/3):277-281.

(责任编辑 杜利民)

GUO Guanping

(CollegeofTeacherEducation,ZhejiangNormalUniversity,JinhuaZhejiang321004,China)

O340

A

1001-5051(2013)02-0166-06

2012-09-26

郭冠平(1960-)，男，浙江东阳人，副教授.研究方向：非线性物理.