再生核方法求解线性Fredholm积分方程组

杨丽宏，旺静然

(哈尔滨工程大学)

0 引言

应用再生核方法求解线性Fredholm积分方程组

其中 a11，a12，a21，a22是常数，并假设方程(1)有唯一解.

Fredholm积分方程在很多方面都有应用.例如 Galerkin法，collocation法，文献［1-4］中的方法等等都给出了Fredholm积分方程的近精确解和近似解.很多研究者对再生核方法进行了研究，因为这个方法容易得到其精确解和近似解，并且有很高的精确度.现在用此方法求解Fredholm积分方程.

1 再生核方法

在该文中，在再生核空间中求出方程(1)的精确解和近似解，并假设方程(1)有唯一解.为了求解此方程组，把方程(1)表示为:

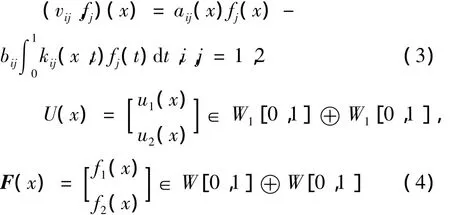
1.1 再生核空间

内积空间 W［0，1］⊕ W［0，1］的定义为:

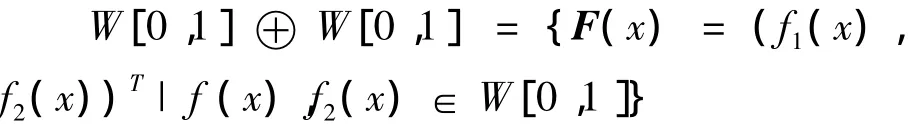
内积和范数定义如下:

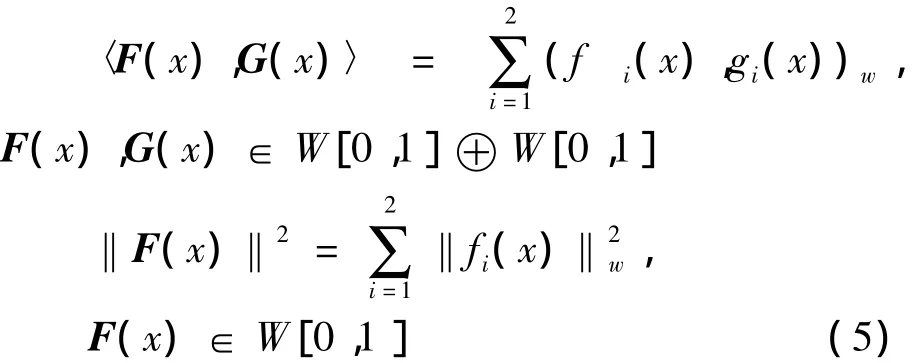
容易证明W［0，1］⊕W［0，1］在定义(5)下是 Hilbert空间.同样，W1［0，1］⊕ W1［0，1］也是Hilbert空间.W1［0，1］和 W1［0，1］空间的定义参见文献［5］.

定理1.1 再生核空间W1［0，1］的再生核函数为:

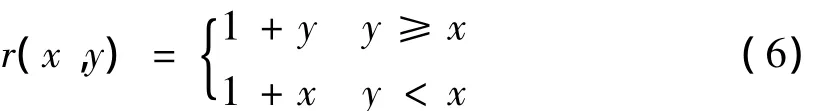
即任意的 x∈［0，1］，f(x)∈ W1，满足(f(x)，r(x，y))W1=f(y).

定理1.2 再生核空间W［0，1］的再生核函数为

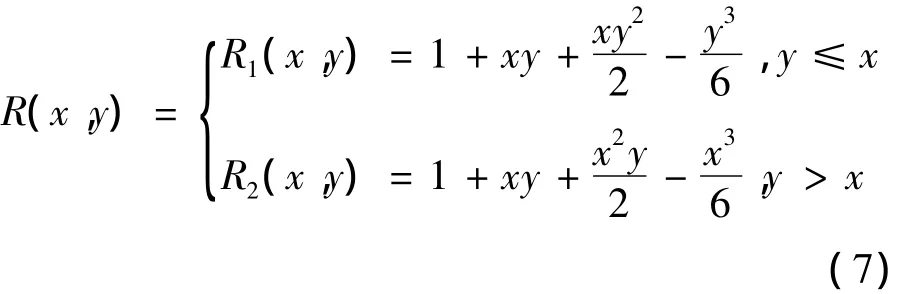
即任意的 x∈［0，1］，f(x)∈ W［0，1］满足(f(x)，r(x，y))W=f(y).

令

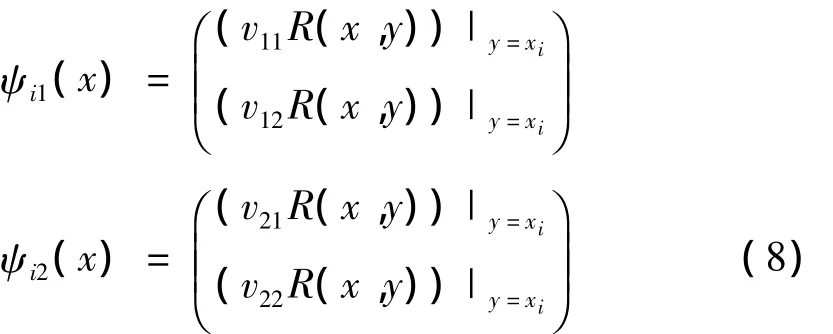
证 明 假 设 {Ψi1j1(x)，ψi2j2}(x)，…，ψikjk(x)}线性相关，令 h={i1，i2，…，ik}，di(y)=r(xi，y)则{Ψij(x)}是线性相关的，即存在cij使得

定理 1.4 在空间 W［0，1］⊕ W［0，1］中，{Ψi1(x)，Ψi2(x)}是完全的.

证 明 0=(F(x)，Ψi1)=v11f1(xi)+v12f2(xi)，0=(F(x)，Ψi2)=v21f1(xi)+v22f2(xi).由的稠密性，所以v11f1+v12f2=0，v21f1+v22f2=0，因此是完全的.

重 新 排 列 {ψ11(x)，ψ12(x)，ψ21(x)，ψ22(x)，ψ31(x)，ψ32(x)…}为{A1(x)，A2(x)，A3(x)，A4(x)，…}，对序列{A1(x)，A2(x)，A3(x)，A4(x)，…}进行Gram-Schmidt 过 程 得 到 序 列即

其中αk=(F(x)，Ak(x))=

证明 根据定理2.4和(9)的Gram-Schmidtz 正交化…，}是正交的，假设F(x)是方程组(1)的精确解，则，其中

定理1.6 截断无穷级数(10)，得到方程组(1)的近似解

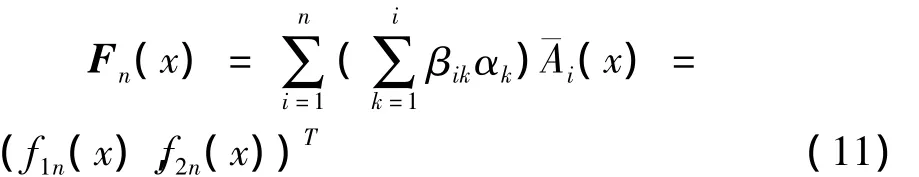
当n→∞时，它一致收敛到精确解F(x)=(f1(x)，f2(x))T.

|fin-fi|=|fin(y)-f(y)，R(x，y)|≤.因此，fin(x)一致收敛到fi(x)，n→∞.

2 数值算例

使用该文构造的数值算法求解线性Fredholm积分方程组

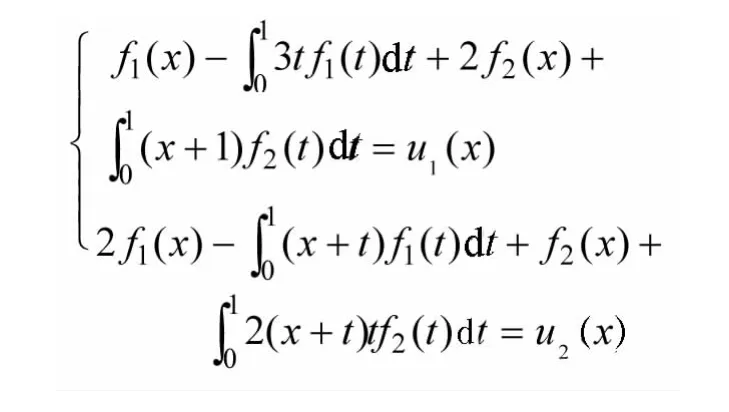
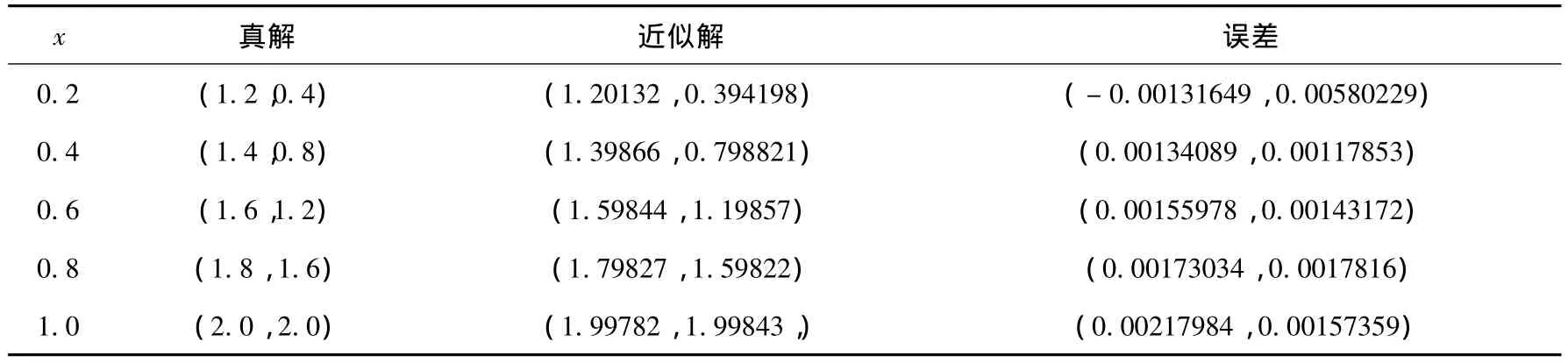
表1 数值结果n=10

［1］ Akyuz A.Dascoglu，Sezer M.Chebyshev polynomial solutions of systems of higher-order linear Fredholm-Volterra integro-differential equations.J.Franblin Inst，2005(342):688-701.

［2］ Brunner H.Collocation Method for Volterra integral and Related Functional Equations.Cambridge University Press，Cambridge，2004.

［3］ Berenguer M I，Gamez D AI.Garralda-Guillem，Ruiz M，et al.Perez，Biorthogonal system for Solving Volterra integral E-quation Systems of the Secondecond kink，kind.Comput J Math，2011，235:1875-1883.

［4］ Farshid Mirzaee，Numerical computational solution of the linear Volterra integral equations systems via rationalized Haar functions.J King Saud Univ(Sci)2010，22:265-268.

［5］ Yang Lihong，Lin Yingzhen.Reproducing kernel method for solving linear initial-boundary-value Problems Differ.Electron J，2008，29:1-11.