R3上的一类非齐次薛定谔-泊松系统解的存在唯一性*

丁 凌， 孟义杰， 张丹丹

(湖北文理学院 数学与计算机科学学院，湖北 襄阳 441053)

R3上的一类非齐次薛定谔-泊松系统解的存在唯一性*

丁 凌， 孟义杰， 张丹丹

(湖北文理学院 数学与计算机科学学院，湖北 襄阳 441053)

用变分方法中的极小定理和一些分析技巧证明了一类非齐次薛定谔-泊松系统在R3上的解是存在的并且是惟一的.

薛定谔-泊松系统；极小定理；解的存在唯一性

考虑如下一类无界区域上的非齐次薛定谔-泊松系统：

(1)

其中u，φ：R3→R，a∈L(R3)，f：R→R是连续函数，h∈L2(R3).此处将研究系统解的存在唯一性性质. 此系统源于物理，根据经典的物理模型，电磁场里带电电荷的相互作用可以用一个非线性Schroödinger方程和一个泊松方程的耦合来描述，这方面的内容可参阅文献[1-3].

到目前为止，有大量的文献研究问题(1). 例如，当φ≡0，系统(1)就退化成单个的Schrodinger方程

-Δu+u+φu=a(x)f(u)+h(x)，x∈R3

(2)

在h(x)≡0(齐次情形)，f的各种情况(超线性、次线性、渐近线性)下都有人研究问题(2)解的存在性[4-6]. 当问题(2)中h(x)≠0(非齐次情形)，解的存在性也有很多人研究[7，8]. 当φ≠0，就是系统(1)；齐次的非齐次的分别见文献[9，10]，都是在f是渐近线性的情况下得到系统(1)的解的存在性结论. 在上述文献中都只研究了解的存在性结论，而在此处将给出系统(1)在下面的假设下可以得到解的存在唯一性结论. 假设如下：

(a)a∈L(R3)，且存在一个常数M，使得a(x)≥M>0 a.e.x∈R3成立.

(b)h∈L2(R3).

(c)f：R→R是一个连续函数，满足

f(t)t≤0，(f(t)-f(s))(t-s)≤0∀t，s∈R

(3)

且存在a，b>0使得

|f(t)|≤a|t|+b|t|2*-1

(4)

采用变分方法对系统(2)进行研究，这种方法是非常有效的方法[11，12].

在给出主要定理及其证明前，先给出一些记号、约化泛函及一些不等式.

H1(R3)，D1，2(R3)是Sobolev空间，范数分别定义为

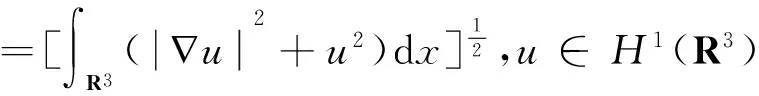
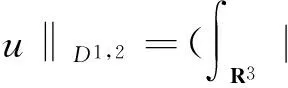
另外记‖·‖p表示Lp(R3)(1≤p≤)范数.系统(1)对应的能量泛函为J：H1(R3)×D1，2(R3)→R，具体表达式为φ|2dx，其中u∈H1(R3)，φ∈D1，2(R3)且F是f的原函数，定义为F(t)=f(s)ds. 根据条件(a)(h)和(f)，显然J∈C1(H1(R3)×D1，2(R3)，R)，且对任意的ν∈H1(R3)，η∈D1，2(R3)，有

寻求系统(1)的解等价于要找对应的能量泛函J的临界点，即(u，φ)是系统(1)的弱解当且仅当它是泛函J的临界点. 而J有两个变量并且是不定的(上方无界且下方无界)，但可以通过约化使得J只有一个变量从而使不定性消失.

对任意的u∈H1(R3)，Lax-Milgram定理[13]暗示了存在唯一的正解φu∈D1，2(R3)，使得-Δφu=u2. 这样把φu代入系统(1)的第一个方程可得

-Δu+u+φuu=a(x)f(u)+h(x)，x∈R3

于是系统(1)就转化成了单个的具有非局部项的非线性Schrodinger方程，并且φu具有显示表达式

(5)

于是就可以考虑泛函I：H1(R3)→R定义为I(u)=J(u，φu). 在等式-Δφu=u2两边乘以φu，再在R3上积分，可得

(6)

把式(6)适当代入泛函J的表达式，得到约化泛函

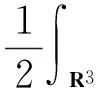
回忆一下最优常数分别记为Sq，S的Sobolev不等式：

‖u‖q≤Sq‖u‖(2≤q≤6)，‖u‖6≤S‖u‖D1，2

(7)

由式(6)、Holder不等式及式(7)可得

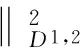
于是可推出

(8)

根据条件式(a)式(b)和式(3)(4)(8)，可得I是C1泛函且对任意的v∈H1(R3)，有

(9)

成立. 因此，如果u∈H1(R3)是泛函I的临界点，则(u，φu)是系统(1)的解且φu满足-Δφu=u2.

主要定理及证明如下：

定理1 假设条件(a)(b)和(c)成立，则系统(1)存在唯一的一个解.

证明因为对任意的u，v∈H1(R3)且u≠v，根据式(9)可得

式(10)(11)相减可得

根据(f)中式(3)及(a)，可得a(x)(f(u)-f(v))(u-v)≤0，于是

根据φu的显示表达式(5)可得(φuu-φvv)(u-v)≥0. 因此有

(12)

成立. 根据Banach空间上的可微泛函，如果满足式(12)，则此泛函是严格凸泛函. 显然H1(R3)是Banach空间且I是C1的，于是不等式(12)暗示了I是严格凸泛函.

另外由式(3)可知

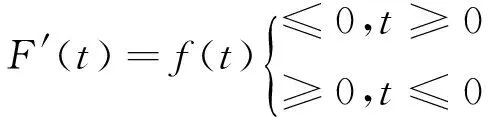
于是F(t)在t<0时是单调递增的，在t>0时是单调递减的，F(t)在0点处取得最大值，即F(t)≤F(0)=0，∀t∈R. 因此，再由(a)，φu的非负性、Holder不等式、式(b)及式(7)可得

(14)

由不等式(14)显然可得：当‖u‖→+，有I(u)→+成立. 即泛函I是强制泛函.

从上面的讨论知道，泛函I是强制的、严格凸的、连续可微泛函，根据变分方法中的全局极小定理，得到泛函I有唯一的极小值点. 即泛函I有唯一的临界点，从而系统(1)有唯一的解.证毕.

[1] BENCI V， FORTUNATO D. An eigenvalue problem for the Schrödinger-Maxwell equations[J]. Topol Methods Nonlinear Anal, 1998(11)： 283-293

[2] AKHMEDIEV N， ANKIEWICZ A，SOTO-CRESPO J M. Does the nonlinear Schrödinger equation correctly describe beam propagation[J]. Optics Lett, 1993(18)： 411- 413

[3] ILLNER R，LANGE H， TOOMIRE B，et al. On quasi-linear Schrodinger systems[J]. Math Meth Appl Sci, 1997(20)： 1223-1238

[4] LIU Z L， WANG Z Q. Existence of a positive solution of an elliptic equation onRN[J]. Proc Roy Soc Edinburgh Sect, 2004(A134)： 191-200

[5] JEANJEAN L. On the existence of bounded Palais-Smale sequences and applications to a Landesman-Lazer-type set onRN[J]. Proc Roy Soc Edinburgh Sect，1999(A129)： 787-809

[6] STUART C A，ZHOU H S. Applying the mountain pass theorem to an asymptotically linear elliptic equation onRN[J]. Comm Partial Differential Equations，1999(24)： 1731-1758

[7] CAO D M，ZHOU H S. Multiple positive solutions of nonhomogeneous semilinear elliptic equations inRN[J]. Proc Roy Soc Edinburgh Sect，1996(A 126)：443- 463

[8] CHEN K J. Exactly two entire positive solutions for a class of nonhomogeneous elliptic equations[J]. Differential Integral Equations，2004(17)： 1-16

[9] CERAMI G， VAIRA G. Positive solutions for some nonautonomous Schrödinger-Poisson systems[J]. J Differential Equation，2010(248)：521-543

[10] SUN J T， CHEN H B，NIETO J J. On ground state solutions for some non-autonomous Schrödinger-Poisson systems[J].J Differential Equation，2012(252)： 3365-3380

[11] 丁凌，孟义杰. 具有Sobolev临界指数的奇异椭圆方程正解的存在性和多重性[J]. 重庆工商大学学报：自然科学版，2008，25(3): 240-242

[12] 丁凌. 在混合边界条件下奇异临界指数的椭圆方程的无穷多个解[J]. 重庆工商大学学报：自然科学版，2010，27(1)： 30-35

[13] GILBARG D， TRUDINGER N S.Elliptic partial differential equations of second order[M]. Reprint of the 1998 edition. Berlin：Springerg,2001

The Existence of Uniqueness of a Solution for a Class of Non-homogenous Schrödinger-Poisson Systems in R3

DINGLing,MENGYi-jie,ZHANGDan-dan

(School of Mathematics and Computer Science，Hubei University of Arts and Science，Hubei Xiangyang 441053，China)

The existence of uniqueness of a solution for a class of non-homogenous Schrödinger-Poisson systems inR3is verified by using the minimum theorem of the variational method and some analysis techniques.

Schödinger-Poisson systems；minimum theorem；existence of uniqueness of a solution

1672-058X(2013)09-0006-04

2013-03-27；

2013-04-20.

国家自然科学基金青年基金(11101347)； 湖北省教育厅科学研究计划重点项目(D20112605; D20122501).

丁凌(1975-)，女，湖北襄阳人，副教授， 博士，从事非线性分析的研究.

O176.3

A

责任编辑：李翠薇