巧用填补法解决大学物理电学非对称问题

魏生贤，邱学云，晏翠琼，何禧佳

（1.曲靖师范学院 物理与电子工程学院，云南 曲靖 655011，2.文山学院 数理系，云南 文山 663000）

在求解物理问题时，常常因某些物理量分布的非对称性使问题复杂化，无法利用公式或定理直接求解，致使问题难以求解，甚至无法求解。填补法又称补偿法，就是使一些非对称分布问题，在与原问题和物理规律不相违背的前提下，适当补充一些物理条件而变为对称分布，使一些定理或公式得以直接应用，将原来较复杂的问题简化，并便于求解的方法［1-4］。因此，填补法在力学、电磁学、物理试验中应用较为广泛。本文就填补法在大学物理电学非对称问题中的应用进行详细分析，具体讨论了填补法在电场强度、电场力、电势、角速度、电通量和电阻求解中的应用。教学中引入填补法，并将其应用于实际问题，可大大简化问题，便于问题的求解和学生逻辑思维能力的培养，可使教学效果事半功倍。

1 利用填补法计算场强

1.1 缺口金属圆环在其圆心处的场强

如图1所示，将金属丝AB弯成半径为R的圆弧，A、B间留有宽度为d的间隙（d＜＜R）。若缺口圆环均匀带电，电荷线密度为λ，试计算圆心O处的场强。

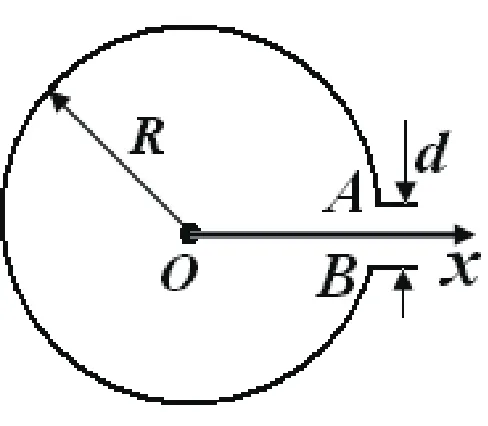
图1 缺口金属圆环

为便于分析，建立如图1所示的极坐标，Ox穿过AB间隙的中心。由于d＜＜R，可将AB间隙带的负电荷-λd视为点电荷［3,6］。据点电荷场强公式可得

场强方向由圆心指向AB间隙中心，即Ox正方向。

1.2 挖去小块面积的均匀带电球面在其球心处的场强

真空中有一半径为R的均匀带电球面，总电量为Q（Q＞0），电荷面密度为+σ，如图2所示。今在球面上挖去非常小的一块面积△S（连同电荷），且假设挖去后不影响原来电荷的分布。计算挖去△S后球心处电场强度的大小和方向。

分析与解答：挖去部分△S的电荷面密度为零，与同时存在面电荷密度+σ与-σ等效。将挖去部分用电荷面密度为+σ的球面补上，使之成为均匀带电球面。此时，球心处的场强是均匀带电球面在球心处的场强与挖去部分（电荷面密度为-σ）在球心处的场强的矢量和，即。

由于Q＞0，球面面电荷密度为σ=Q/（4πR2）。由于球面的电荷均匀分布，由静电场中的高斯定理可知均匀带电的球面在球心处的场强=0，所以由于挖去部分△S较小，可视为点电荷［8］。为便于分析，建立图3所示的极坐标，O点位于球心，Ox穿过△S的中心。由△S上的负电荷激发［7-8］，则

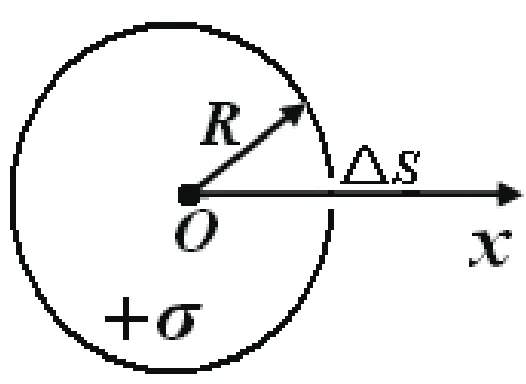
图2 挖去小块面积的均匀带电球面

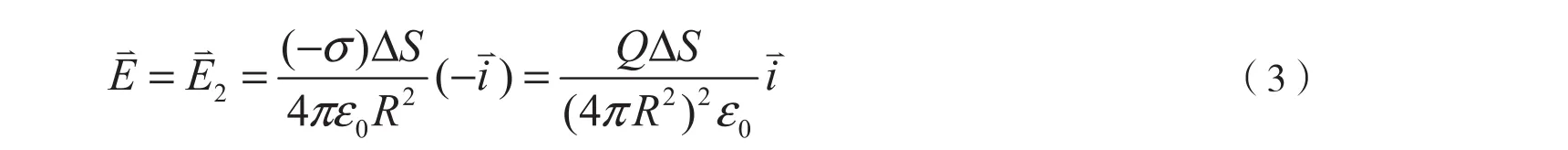
除上述两种情况以外，还可利用填补法与高斯定理结合求解无限大均匀带电平面圆孔轴线上一点的场强［9-10］，均匀带电偏心球壳内外的场强［9，11-13］。

2 利用填补法计算电场力

在球心为O、半径为R1、电荷体密度为ρ的均匀带电球体内偏心地挖去一个半径为R2的带电小球（球心为O '），形成如图3所示空腔球体。设，试计算空腔内任意一点电荷q所受的电场力［14］。

分析与解答：将挖去小球的空腔视为是在原来均匀带电+ρ的球内，填进一个均匀带电-ρ的小球而构成的。由叠加原理，空腔中任意一点电荷q所受的电场力可看成是没有空腔且电荷体密度ρ均匀分布的带电球体对点电荷q所施的电场力与体电荷密度为-ρ的空腔球部分对点电荷q所施加的电场力之叠加，即

图3 偏心球壳内点电荷的电场力

上式显示，点电荷q在空腔内受到恒力的作用。

3 利用填补法计算电势

如图3所示，一半径为R1的球体均匀带电，电荷体密度为ρ，球内有一半径为R2的球形空腔，空腔中心O '与球心O相距为c。试计算空腔中心O '处的电势。

分析与解答：根据上一节的分析可知，球形空腔为匀强电场，场强，其中表示O至O'的距离。由填补法分析可知，空腔中场点P的电势是半径为R1、电荷体密度为ρ的大球和半径为R2、电荷体密度为-ρ的小球产生的电势之和，即Vp=V1+V2。

取无限远处的电势V∞=0，大球电场分布为［9，15］

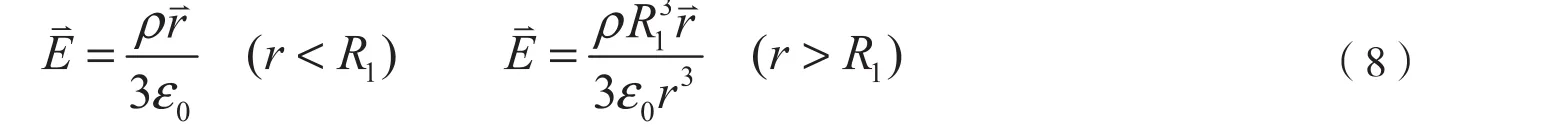
利用电势的定义，可得大球内任一点的电势为

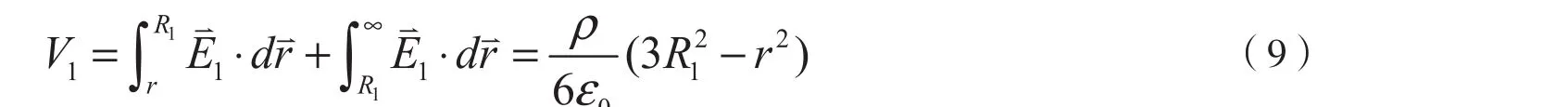
对于空腔中心O '右r=c，则大球产生的电势为

同理，可得小球在O '处产生的电势为

由电势叠加原理可得点O '处的电势为

4 利用填补法计算角速度

如图4所示，一个绝缘的刚性细圆环，半径为R，质量为m，可以绕垂直于纸面的轴O自由旋转，但不能平动。此环长度均匀带电，电荷量为Q。在A点剪下一个小缺口，其空隙长度为l（l＜＜R）。开始时圆环静止不动，接通一个匀强电场E，让E既垂直于轴O，又垂直于半径OA。试计算圆环旋转的最大角速度。

分析与解答：若该细圆环没有缺口，由于受到的合力矩为零，将不旋转。如果将缺口处的不带电看成是单位长度带电情况和圆环带电情况相同的正负电荷的叠加所致，因为l＜＜R，即可将缺口处的电荷认为是点电荷。因此，有缺口的带电细圆环就可等效为一个电荷线密度为Q/2πR的均匀带电圆环和一个带电荷量q=Ql/2πR的负点电荷在缺口处的叠加。显然，电场只对负点电荷产生力矩，当点A顺时针转过90°时，电场力对它做功最多，对应速度最大，即圆环的角速度最大［16］。

根据动能定理有

图4 缺口线圈角速度的计算

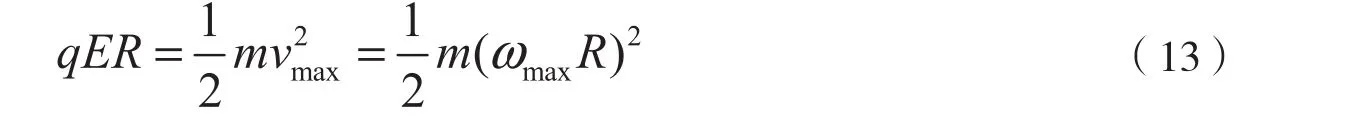
故缺口带电圆环的最大角速度为

5 利用填补法计算电通量

如图5所示，在边长为a的正方形平面的中垂线上，距中心O点a/2处，有一电量为q的正点电荷，试计算通过该平面的电通量。

分析与解答：依据题意，正方形平面各面元与源电荷q的距离不等，无法直接利用公式计算q的场强通过该平面的电通量。但可用6个边长为a的正方形平面将q包围起来，构成一个边长为a的正六面体的闭合曲面，q位于正六面体的中心。由高斯定理可知，通过任意闭合曲面的电通量等于该闭合曲面包围的电荷的代数和的1/ε0倍。对于此问题，通过正六面体构成的闭合曲面的电通量为q/ε0。由于q位于正六面体的中心，则通过正六面体任意一个面的电通量为总电通量的1/6，即为q/（6ε0）。

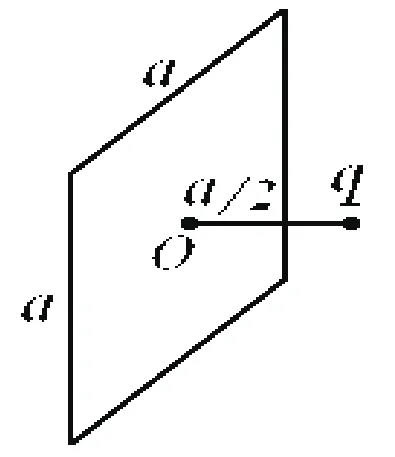
图5 电通量的计算

6 利用填补法计算电阻

如图6所示，P是一块均匀的半圆形薄电阻片，先将它按图6（a）中的方式连接在电极A、B间，测得其阻值为R。试问：将电阻片P按图6（b）的方式与电极A、B相连，其电阻值Rx是多少？

图6 填补法计算电阻值

分析与解答：此题若用积分法则较难求解，用填补法却能轻易求解。若将图6（a）的半圆形薄电阻片填补成图6（c）的方式，它相当于两阻值为R的电阻的串联，其等效电阻值为2R。将图6（c）中的电阻片顺时针旋转90°可得图6（d），在图6（d）中，此圆形电阻片的阻值仍为2R，但它相当于两个P片的并联，即有［4］

以上结果与通过分割法得到的结果一致［5］。

7 结束语

本文利用填补法对大学物理电学中的非对称物理量（场强、电场力、电势、角速度、电通量和电阻）进行了实例分析与解答。分析表明，利用填补法可将非对称物理问题化为对称的物理问题，便于公式或定理的直接应用。教学中应重视科学方法的教学，将填补法应用于教学，引导学生运用科学的分析方法解决实际问题。一方面可起到拓宽思路，使教学效果事半功倍；另一方面有利于学生探索能力和解决问题能力的培养。

［1］段培同，韩彩芹.补偿法在力学和电磁学中的应用［J］.泰安师专学报， 2002（3）： 46-48.

［2］李效峰.补偿法在物理学中的应用［J］.吉林建筑工程学院学报，2008（1）： 102-104.

［3］李蓉蓉.补偿法在物理学中的应用［J］.南通工学院学报，1998（2）： 21-23.

［4］周继芳.浅析补偿法在物理题解中的应用［J］.西南民族大学学报：自然科学版， 2004（6）： 859-862.

［5］魏嵋.巧用物理模型解题方法初探［J］.甘肃教育学院学报：自然科学版，1999（S2）：62-64.

［6］胡军权.浅析应用“填补法”构建物理模型［J］.常熟高专学报，2003（6）：121-122.

［7］孙迺疆，胡盘新.普通物理学（第六版）习题分析与解答［M］.北京： 高等教育出版社，2006：160-167.

［8］申绪英.浅谈填补法在解决物理问题中的重要作用［J］.四川工业学院学报， 2002（ S1）： 107-108.

［9］崔觉梅，成城，王晓颖.大学物理学习指导［M］.西安： 西安电子科技大学出版社， 2002：71-82.

［10］马新莉.物理解题技巧—补偿法探讨［J］.理工高教研究，2003（2）： 83-84.

［11］房淑芬.电磁学中一种有用的解题方法［J］.辽宁师专学报， 1999（3）： 25-28.

［12］刘海英，何南.模型转换在普通物理解题中的应用［J］.桂林师范高等专科学校学报， 2010（3）： 187-189.

［13］张三慧.大学基础物理学（第2版）教师用书（习题详解）［M］.北京： 清华大学出版社， 2007:125.

［14］刘成有.填补法在物理教学中的应用［J］.广东职业技术师范学院学报， 1999（4）：92-96.

［15］林福忠.用补偿法巧解物理题［J］.龙岩师专学报， 2004（3）： 97-98.

［16］肖建华.巧解竞赛题的一种方法——“补偿法”［J］.物理通报， 2011（4）： 48-50.