Akima曲线插补中的空间曲线多项式生成方法研究

来燕菁 张为民 齐党进 黄云鹰

（①同济大学机械与能源工程学院，上海 201804;②同济大学沈阳机床研究院，上海 201804）

Akima算法是Hiroshi Akima于1970年提出的一种新的曲线插值算法，它是一种在已知数据点间建立一阶导数连续的分段三次多项式算法，通过与常用的多项式插值算法、三次样条算法和密切插值算法比较，它的计算更简便，并且生成的曲线也更平滑自然［1］。目前这种算法广泛且主要应用于实验数据的分析处理中，日本著名的数据分析及可视化软件KyPlot就于2008年将Akima算法囊括于它的5．0版本中。而在机床数控系统的开发领域，国外的知名数控系统，如德国西门子的840D数控系统，已将Akima算法实现为插补算法，并简称它为A－Spline，但该项插补技术在国内还处在起步研究阶段，相关文献成果较少。由于目前实现的数控机床自由曲线插补算法大多计算过程复杂，给计算能力有限的机床数控系统带来压力，而Akima算法的计算效率高且其所生成的曲线具有唯一性和平滑性，因此考虑将它实现为机床数控系统适用的插补算法，以提高数控系统的插补效率。该插补算法将主要适用于要求加工曲线依次经过给定型值点的自由曲线快速插补。

由于Akima算法原理描述平面曲线，而数控机床多要求实现空间曲线的加工，因此要实现数控机床的Akima曲线插补，首先要应用Akima算法原理描述出空间曲线的表达式。通常空间曲线的描述有一般方程（即将空间曲线理解为空间两曲面的交线）和参数方程两种方法，显然，在数控系统运算中后者更容易控制和实现，同时也便于Akima算法的应用。部分文献应用［x，y（x），z（x）］来描述空间曲线，即采用建立y－x和z－x的关系式来描述空间曲线。虽然这种方法只需按照一定算法规则建立两次关系式，计算量要小，但它不便于处理无穷大斜率（如，y=y（x）的斜率为dy/dx，当其无穷大时难以表示，若采用参数方法，则该斜率为dy/dx=（dy/du）/（dx/du），表示斜率无穷大时只需令dx/du=0），也不便于处理多值曲线［2］。而通过参数化方法获取参数与x、y、z分别建立关系式的描述方法，不但可以克服以上缺陷，还能够保证几何不变性，且易于进行坐标变换。本文即采用这种空间曲线描述方法，通过对常用参数化方法的研究，选取两种常用的参数化方法，并经过Matlab仿真验证其可行性和比较两者的实现效果。

1 Akima算法的基本原理简述［1］

Akima算法即Akima分段三次多项式，是在每两个数据点间建立一条由三次多项式拟合而成的曲线，整条曲线保证一阶导数连续。该算法也被称为五点光滑插值法。

给定n个型值点{（xi，yi）}，i=1，…，n按x坐标升序排列，根据已知条件

可以在任意两相邻型值点（xk，yk）和（xk+1，yk+1）间唯一确定一个三次多项式:

其中，

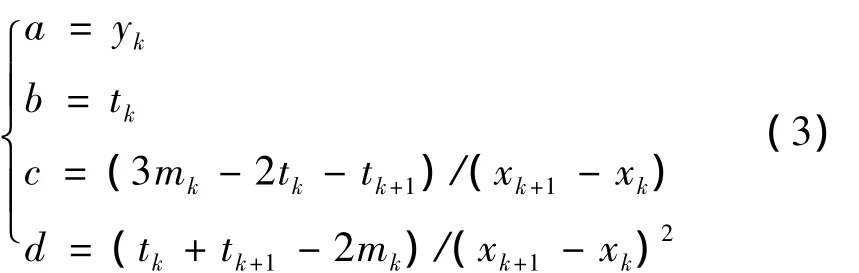
相邻两型值点间线段的斜率

因计算切线斜率需要，补充m0=2m1－m2，m－1=2m0－m1，mn=2mn－1－mn－2，mn+1=2mn－mn－1。

型值点（xk，yk）处的切线斜率:

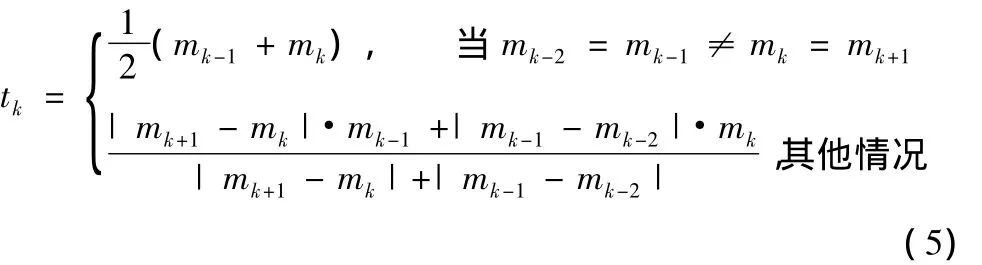
2 空间Akima曲线多项式的生成方法

为实现数控机床Akima曲线插补算法，首要任务是解决空间Akima曲线多项式的生成。为更好适应自由曲线类型，应采用参数方法描述Akima空间曲线，具体实现方法分为两个步骤。

第一步，根据给定型值点Pi（xi，yi，zi），i=1，…，n获取参数ui，即参数化。

第二步，应用Akima算法的基本原理来分别构造x－u、y－u和z－u的Akima关系式来描述空间曲线（式6）。

经过这两个步骤获得的空间Akima曲线多项式，在应用到机床数控系统进行插补时，便可以顺序在［uk，uk+1］区间内插值获取加工点的三坐标值，完成曲线的加工。明确空间Akima曲线多项式的生成步骤后，不难看出参数化方法的选取直接影响后续Akima空间曲线的生成，应合理选取参数化方法。

目前参数化主要有均匀参数化方法（适合于数据点多边形各边接近相等的场合）、累加弦长参数化方法（大多数情况下所得曲线具有较好的光顺性）［3］、向心参数化方法（为体现曲线折拐情况而提出，但实验结果未完全体现）、修正弦长参数化方法（即Foley－Nielson参数化，综合考虑弦长和相邻线段夹角，引入修正系数以修正曲率较大处弦长与实际弧长偏离较大的缺陷）［4］。为适应大多数情况，本文选取累加弦长参数化方法（以下简称累加法）与修正弦长参数化方法（以下简称修正法），在Matlab（版本7．0，运行环境为WindowsXP）软件上分别与Akima算法结合实现仿真和比较。

2．1 两种参数化方法的参数计算公式

给定型值点Pi（xi，yi，zi），i=1，…，n，则与Pi相对应的累加弦长参数为:

而与型值点Pi相对应的修正弦长参数为:

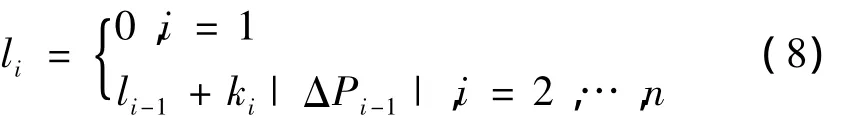
其中，

修正法中引入的修正系数ki≥1。与前后相邻弦长|ΔPi－2|和|ΔPi|比，若弦长|ΔPi－1|越小，且与前后相邻弦线夹角的外角 θi－1、θi（不超过 π/2）越大，则修正系数ki越大，因而修正弦长即参数区间Δli－1=ki|ΔPi－1|也越大，这样对因该曲线段绝对曲率偏大，实际弦长偏短的情况起到了修正作用，修正弦长就较接近于实际弧长［5］。

2．2 实验说明与结论

为实现两种参数化方法效果的清晰比较，本文选取平面内的正弦线和空间内椭圆线模型各一，综合考虑数控机床的实际加工情况，从两模型理论曲线中抽取型值点，分别用两种参数化方法的Akima算法插值获得曲线，并逐一进行比较。

（1）正弦线模型的实验比较

从长度约为1 054 mm的正弦线:

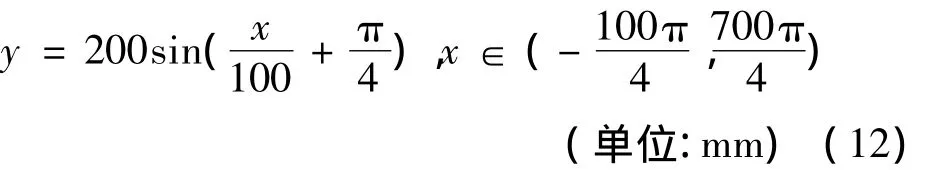
上按x坐标等距选取17个型值点（见表1，点平均间距65.88 mm），分别运行两种参数化方法对应的Akima算法Matlab程序进行实验。实验结果显示:两种参数化方法结合Akima算法后都能够较好地描绘出与理论正弦线形状一致且误差不大的曲线;通过比较两种参数化方法经Akima插值获得的曲线点与理论点在相同x坐标处的y坐标误差值Δy的曲线图（如图1所示），相邻型值点间曲线段的Δy最大值列入表1中，可以发现修正法经Akima插值获得的曲线更接近理论正弦线，且误差波动小，其平均Δy误差为0.259 1 mm，最大误差控制在0.8 mm以内，而累加法的平均Δy误差为0.397 6 mm，最大误差在1.2 mm以内，因而修正法优于累加法;由于修正法计算参数时需要算出修正系数，因而程序较累加法复杂一些，其算出Akima曲线数据点的所需时间为0.235 s，而累加法所需时间则少一些，为0.218 s。

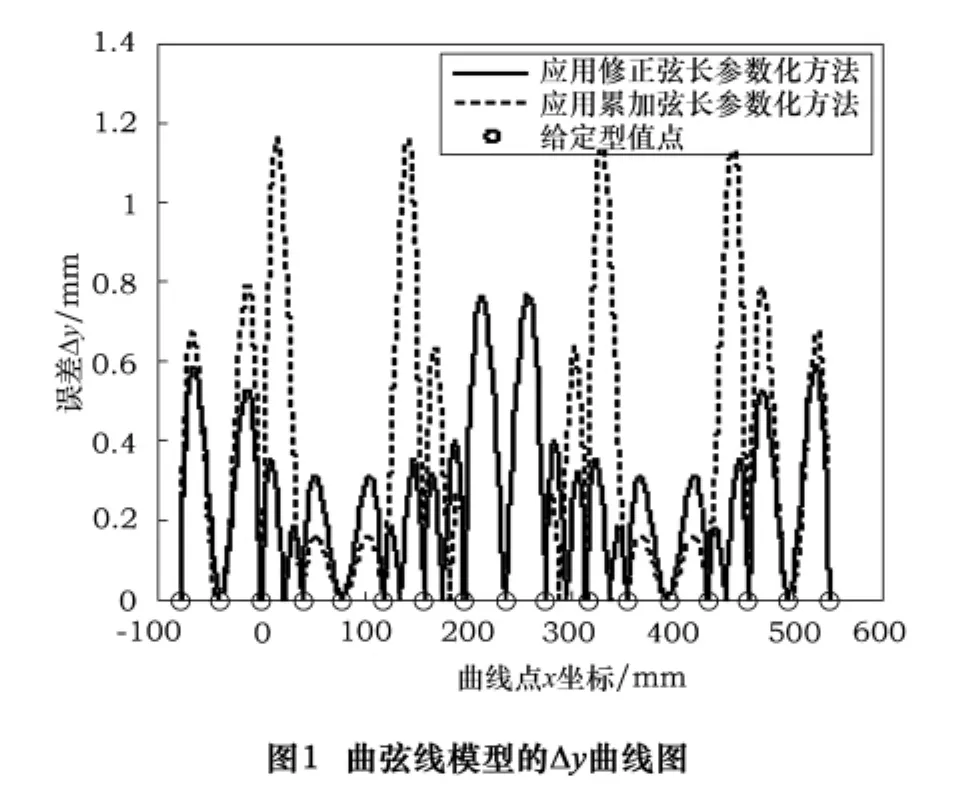
表1 正弦线模型的实验结果

另做实验，将型值点数据多取一倍，取33个点，点平均间距32.94 mm，两种方法生成的曲线均将误差缩小约一个数量级，其中修正弦长法可将误差Δy的平均值缩小至0.036 2 mm，而累加弦长法则为0.047 1 mm，修正法仍然优于累加法。

（2）椭圆模型的实验比较

从椭圆线:

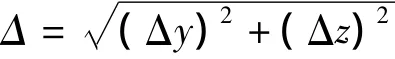
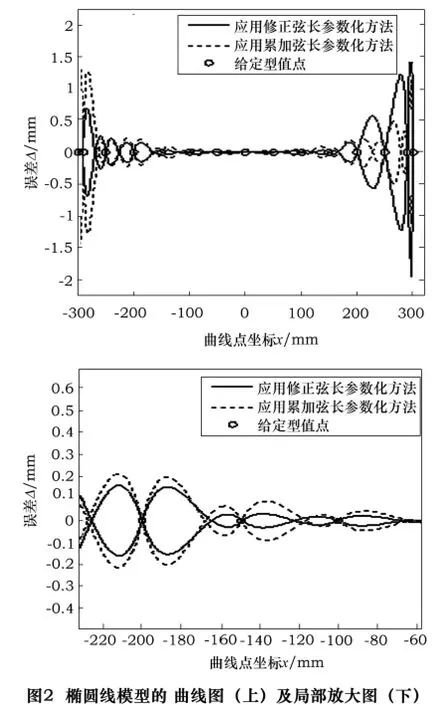
综合以上实验结果，可以得出以下结论:

（1）在获取Akima曲线多项式参数的两种常用参数化方法中，修正法相比于累加法总体上更接近理想曲线，且误差波动相对稳定。

（2）由于修正法计算参数时需要计算修正系数，因而相对于累加法要复杂些，耗费时间要多。

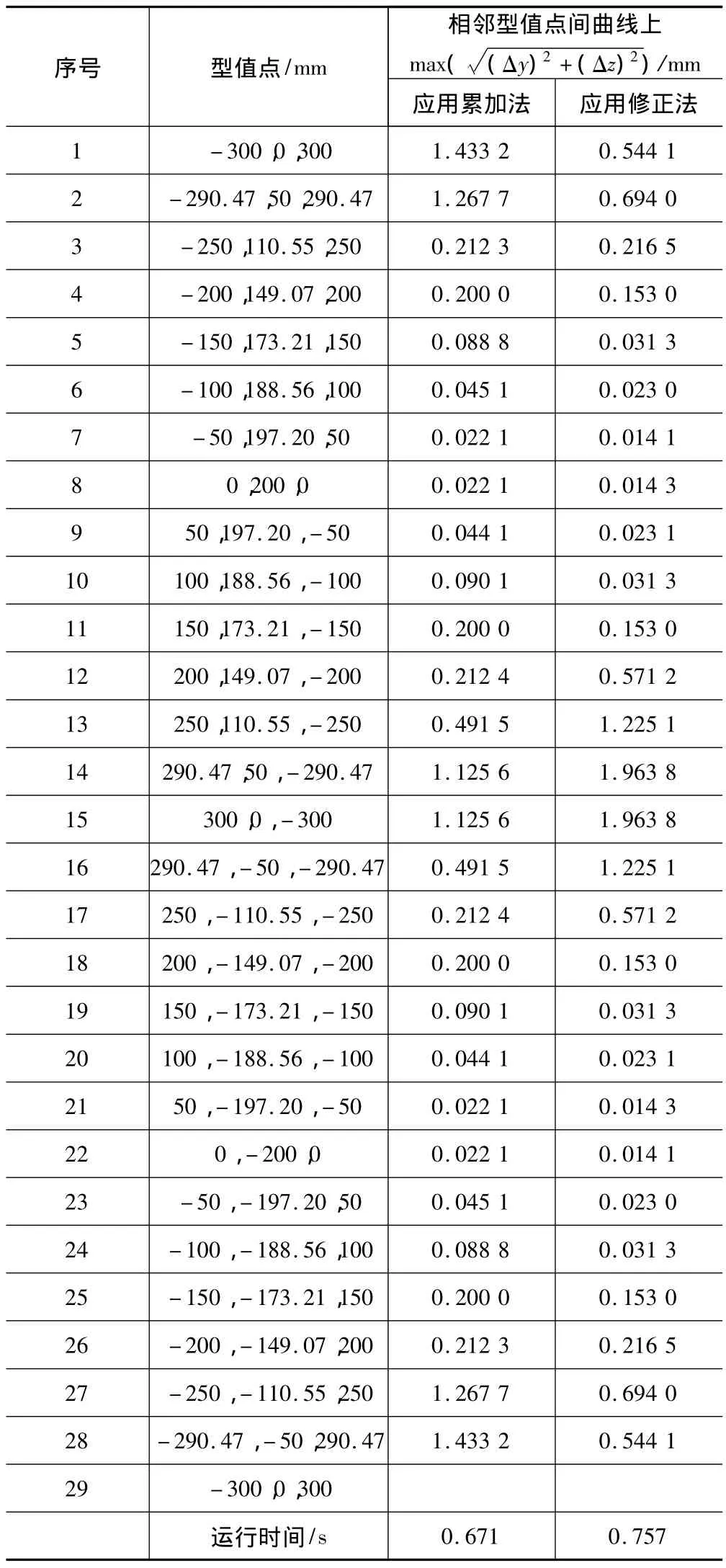
表2 椭圆线模型的实验结果

因此，在数控系统运算能力允许的情况下，建议在进行空间Akima插值曲线计算时选择修正弦长参数化方法来获取参数。

3 结语

本文对数控机床Akima曲线插补实现中的首要步骤——Akima空间曲线表达式生成方法进行讨论，成功将Akima算法的基本原理通过参数化方法扩展为描述空间曲线，并通过Matlab软件实现仿真，完成实验对比累加弦长参数化方法和修正弦长参数化方法下Akima算法的曲线生成效果，实验结果发现修正弦长参数化方法总体优于累加弦长参数化方法，但计算要相对复杂些，在数控系统运算条件允许的情况下，建议优先选择修正弦长参数化方法。

［1］Hiroshi Akima．A new method of interpolation and smooth curve fitting based on local procedures［J］．Journal of the Association for Computing Machinery，1970，17（4）:589－602．

［2］朱心雄．自由曲线曲面造型技术［M］．北京:科学出版社，2000．

［3］于辉．参数曲线数据点参数化方法的研究［D］．济南:山东大学，2009．

［4］罗钟铉，孟兆良，刘成明．计算几何——曲面表示论及应用［M］．北京:科学出版社，2010．

［5］施法中．计算机辅助几何设计与非均匀有理B样条［M］．北京:高等教育出版社，2001．