考虑犁切力的微铣削颤振稳定域建模与分析*

曹自洋 李 华 殷 振 谢 鸥

（苏州科技学院机电工程系，江苏苏州 215011）

微细铣削加工技术具有可加工多种材料、生产柔性大、兼具高精密和超高速加工的特征，对微三维零件的加工具有独特优势［1－3］。但是，微细铣削过程中常常发生切削颤振的动态不稳定现象，其产生源于刀具和工件之间的相互振动，由于上次切削所形成的振纹与本次切削的振动位移之间的相位差导致切屑厚度的不同而引起的自激振动。切削系统引发的加工颤振会明显降低切削效率与零件的加工质量，降低刀具、机床的使用寿命，已经成为阻碍该技术发挥其优势的主要瓶颈之一［2－4］。

在宏观铣削的颤振分析模型中，由于工件尺寸较大，选用的每齿进给量同临界切屑厚度相比要大很多，此时切削加工一般处于切削作用机制。然而，微细铣削加工时每齿进给量通常仅有乃至小于几个微米，而微铣刀通常有几个微米的切削刃钝圆半径，微铣削过程中的每齿进给量大致等于甚至小于刀具切削刃钝圆半径，此时形成较大的负前角。当切削加工过程从宏观转到微观时，刀齿在每个旋转周期，随着切屑厚度的大小随瞬时转角的变化，微细铣削加工存在犁切、剪切两种不同的切削方式，切削加工从以剪切为主变化到犁切－剪切相互作用的机制［1－5］。当瞬时切屑厚度大于临界切屑厚度时，铣削加工以剪切为主;当瞬时切屑厚度小于临界切屑厚度时，铣削加工以犁切为主。而且犁切力会引起综合切削力的增大，并引起加工过程振动，从而导致加工质量的恶化。但是，犁切力对微细铣削颤振的影响还没有得到很好的研究。

目前，研究者已经对宏观铣削加工的颤振做了深入的研究，基本能够对颤振进行预测和抑制。Salahshoor［6］通过数值分析对铣削颤振进行了系统的研究，但是他并没有考虑铣削加工的动态特性。Huang［7］对宏观尺度颤振进行了理论建模，并考虑了加工阻尼力对圆周铣削颤振的影响。Altintas［8］通过加工实验并结合理论分析对铣削颤振进行了时域建模，但是他利用每一个刀齿旋转周期的平均切削力进行建模，这与实际加工不相符合。Budak［9］通过跨尺度建模对车削的颤振稳定性进行了理论研究。山东大学的宋清华［10］借助理论分析和实验研究，对高速铣削的稳定性进行了系统的研究。为了抑制加工颤振，上海交通大学的江浩［11］以铣削加工为研究对象，设计了一种用于铣削减振的两自由度工件装夹平台。上述研究在对切削加工过程建立动力学模型时，和实际的加工过程差距较大，具体表现在实用性差、考虑铣削力因素不全面、研究范围不够宽、软件仿真时的模型过于简单，而且研究仅限于宏观尺度的加工颤振，很少涉及到对微细铣削颤振稳定性的研究。

微细铣削加工与常规切削、精密切削的机理截然不同，常规尺度铣削颤振的力学模型、分析工艺模型和预测模型等不再适用于微细铣削加工，必须考虑微细铣削的工艺特点和切削机理重新进行理论和实验研究。

1 微铣削稳定性时域建模

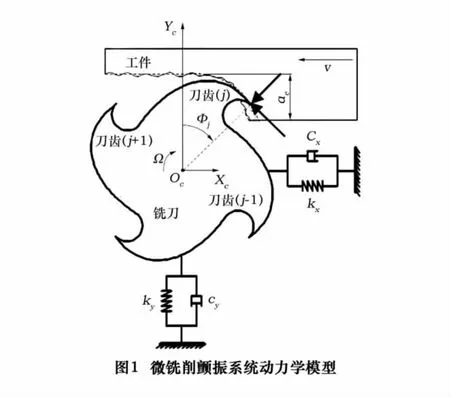
将铣削过程简化为两自由度弹性－阻尼系统，通过研究刀尖的动态位移来研究铣削颤振，其系统动力学模型如图1所示。由于微细铣削的轴向切深非常小，所以铣刀螺旋角对加工的影响很小，模型中忽略了轴向力的影响。

其中:Mx、My、Cx、Cy、Kx、Ky分别为X、Y方向上机床－刀具系统的质量、阻尼和刚度;Fx、Fy分别为综合切削力在X、Y方向上的分量。

通过拉普拉斯变换，式（1）、（2）可以改写为:

其中:φx、φy是刀尖在X、Y方向的动态特性，可表示为:

其中:n是加工系统模态的阶数。

再生型颤振主要是由动态切屑厚度的再生效应所致，它是切削过程瞬时转角的函数。可再生的动态切屑厚度h可表示为:

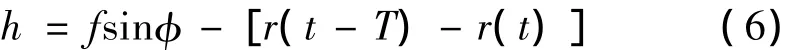
其中:f是进给量;φ为转角，φ=ωt;ω为角速度;T是刀齿切削周期;r是刀尖径向的位移。由于切屑厚度的静态组成部分对动态切削再生机理不起作用，所以在函数中不予考虑。

从图1可以得出，刀尖的径向位移r可以表示为X、Y方向位移的函数:

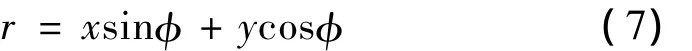
2 犁切力和剪切力建模

在宏观的铣削加工过程中，一般情况下每齿进给量都比临界切屑厚度大得多，所以犁切力对宏观切削加工的影响可以忽略不计。但是在微细铣削加工中，在刀齿的每一个切削周期，剪切力和犁切力总是相伴发生，尤其是在每齿进给量很小的工况中。刀齿在每个旋转周期的切削过程见图2。

从图2可以看出，当刀齿从A点切入工件，此时切屑厚度为零;当刀齿到达B点的时候，切屑厚度也相应达到了临界切屑厚度。在这个过程中，刀具和工件之间相互摩擦、挤压，并没有切屑的产生。A－B区间犁切力的大小可以依据刀具－工件之间相互作用体积的大小来建模。刀齿通过B点之后，实际切屑厚度变得比临界切屑厚度大，就开始形成切屑，进入剪切作用机制。

由此可见，当切屑厚度小于临界切屑厚度的时候，刀具较大的负前角和刀具－工件之间的弹性回复明显影响犁切力的大小。当切屑厚度大于临界切屑厚度的时候，起主要切削作用的是剪切力。所以整个铣削过程就反复在犁切和剪切之间相互转换。为了方便分析，假定从犁切到剪切的过渡是瞬时完成的。在剪切效应主导的区域，切削力的建模与宏观切削加工一致。因此，根据切屑厚度与临界切屑厚度的大小关系，切削力和犁切力建模如下:

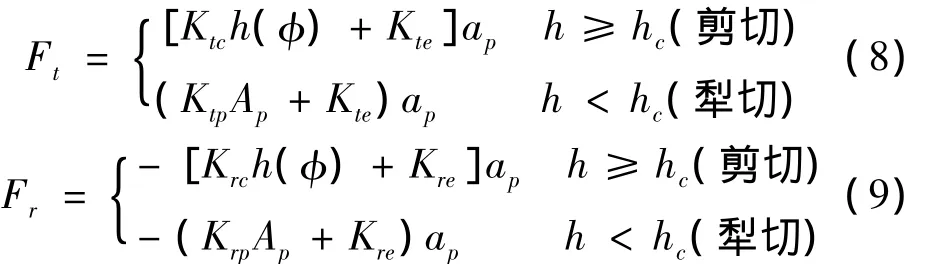
式中:ap是轴向切削深度;h是切屑厚度;Ktc、Krc是切向和径向的切削系数;Kte、Kre是切向和径向的刃口力系数;Ktp、Krp是切向和径向的犁切力系数;Ap是刀具和工件之间的切削面积的大小，可表示为:

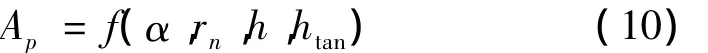
其中:α是刀具后角;rn是刀具的切削刃钝圆半径;h是切屑厚度;htan是弹性回复厚度。

最终，根据切向力、径向力和瞬时转角，X、Y向的切削力可以表示为

为了计算X、Y向的切削力，首先需要通过铣削加工实验得出切削力和犁切力系数。

3 微铣削实验

加工实验采用三轴联动微细铣床，加工方式为铣削直槽，工件材料为硬铝（2A12），实验微铣刀采用瑞士Fraisa公司的直径为0.5 mm的硬质合金两刃平头立铣刀，刀具切削刃钝圆半径rn约为5 μm。切削力的测量采用三向力传感器（PCB260A01），实验装置如图3所示。

实验得出的切削系数和犁切系数Ktc为2 120 N/mm2，Krc为 1 680 N/mm2，Ktp为 850 kN/mm3，Krp为1 245 kN/mm3。

4 颤振稳定域时域求解

本文采用时域仿真来研究在不同切削深度、进给速度和主轴转速组合下的铣削加工稳定性。铣削时域仿真的流程如图4所示。

从图4可以看出，时域仿真过程首先要确定刀齿在每个瞬时转角所对应的名义切屑厚度h0（h0=fsinφ），然后根据式（6）计算实际的切屑厚度。在计算得到实际切屑厚度的基础上，X、Y方向上对应每个瞬时转角的切削力、犁切力可根据式（8）～（11）计算得到。如果切屑厚度小于设定的临界切屑厚度，就按照犁切作用机制的公式求解;如果切屑厚度大于设定的临界切屑厚度，就选用剪切公式求解。基于式（3），X、Y方向上对应的位移由相应的切削力和动态特性确定。然后综合X、Y方向上的位移值，由式（7）计算得到刀尖的径向位移。仿真过程还设置了一个延时函数e－sT，用来补偿当前切削刀齿和上一个刀齿之间的相位差。

目前基于颤振模型的时域微分方程求解多采用欧拉方法，但这种方法更适合于低阶方程的求解。而龙格－库塔（Runge－Kutta）方法是一种求解高阶微分方程的高精度单步方法，其收敛性与稳定性都要高于欧拉方法。因此本研究采用4阶龙格－库塔公式来求解微分方程。

对应于每一个设定范围的主轴转速，仿真程序自动地对轴向切削进行计算，扫描整个转速区间就得到颤振稳定域图。传统的颤振分析方法，是基于定向的传递函数，把对应于一个特定转角的所有切削力和位移表示在一个平面中。而本研究是对应于每一个瞬时转角对刀尖的动态位移进行建模，所以本研究时域仿真的分析精度更高，也更符合实际的铣削工况。

5 结果和讨论

为了研究犁切效应对铣削颤振的影响，首先要确定临界切屑厚度，而临界切屑厚度与刀具切削刃钝圆半径紧密相关。实验中采用微铣削铣刀的钝圆半径为5 μm，硬铝铣削加工的临界切屑厚度大约为刀具钝圆半径的0.25倍，所以犁切和剪切的相互转换的临界切屑厚度约为1.25 μm。为此，本研究设定两个每齿进给量，分别为1 μm和10 μm，在这两种工况下，起主要作用的分别是犁切机制和剪切机制。

根据建立的颤振分析模型进行数值分析，不同进给速度下的铣削加工颤振稳定域时域仿真结果如图5所示。

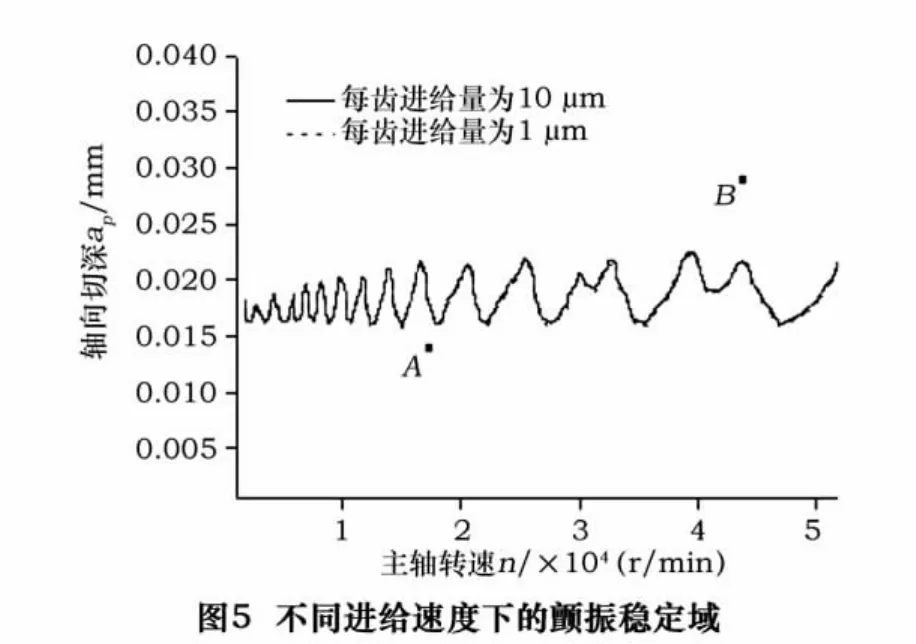
图5所示图线下方为切削稳定区，图线上方为颤振区。从图5可以看出，在每齿进给量分别为1 μm和10 μm的加工条件下，铣削颤振稳定域的仿真结果并没有明显的不同。尽管由于犁切力的作用会造成总切削力的显著增大，但是犁切效应对于铣削加工颤振不稳定现象的影响非常小。这可能是由于在不同的进给速度下，犁切效应对刀尖径向位移的影响非常小。也就是说，犁切力的静态方面对动态颤振稳定性的影响可以忽略不计。

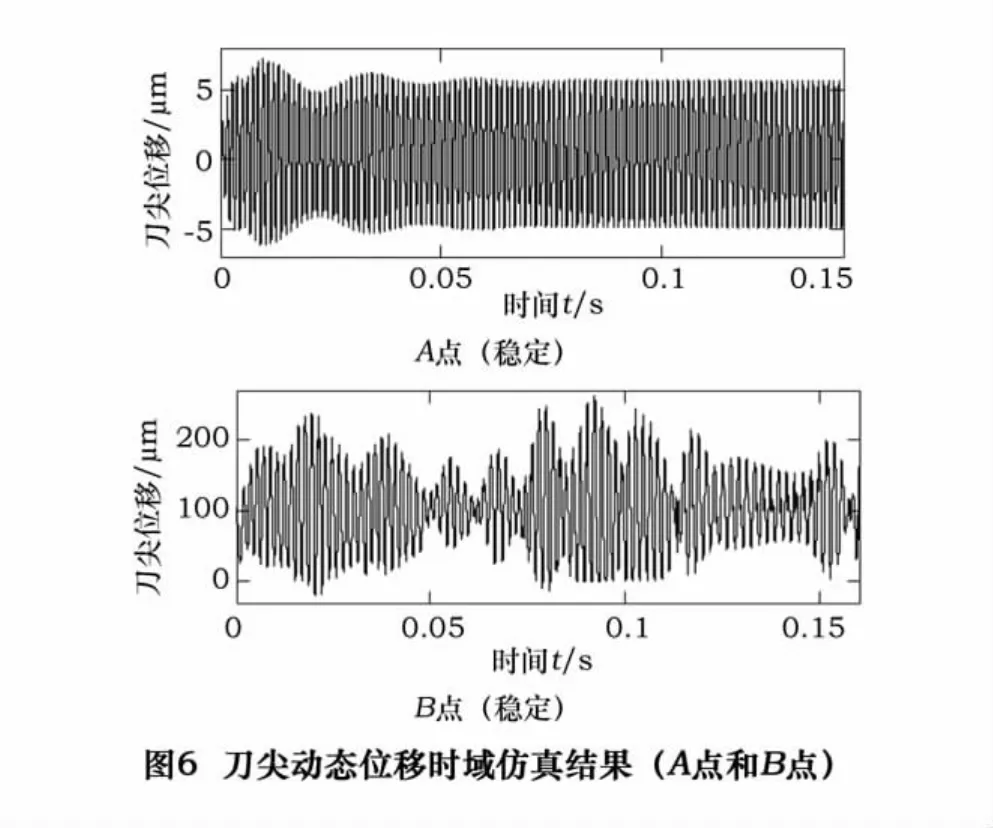
为了进一步研究刀尖的振动情况，当每齿进给量为1 μm时，分别选取处于稳定加工状态的A点和处于颤振区的B点进行时域仿真，得到刀尖动态位移的仿真结果如图6所示。

从图6可以看出，处于稳定区A点的振动信号非常稳定，幅值最大只有约5 μm，加工中能够获得较长的刀具寿命和较好的加工质量。但是处于颤振区B点的刀尖位移加工中瞬间增大到200 μm左右，而且振动信号的幅值波动很大。在实际的工况中，这种加工不稳定现象将会造成刀具严重偏离工件表面，引起刀具的损坏和零件的加工误差。

6 结语

（1）建立了微观尺度下考虑犁切效应的微铣削动态铣削力模型和颤振稳定域解析模型。

（2）在微铣削加工实验的基础上，对应于刀齿的每一个瞬时转角，对微铣削颤振稳定域进行了时域求解，研究了犁切效应对颤振稳定域的影响。

（3）微铣削时域分析结果表明犁切效应对微细铣削过程的加工不稳定现象没有显著的影响。

［1］Chae J，Park SS，Freiheit T．Investigation of micro－ cutting operations［J］．International Journal of Machine Tools and Manufacture，2006，46:313－332．

［2］Chae J．Development and analysis of the precision micro milling system［D］．Alberta:University of Calgary，2006．

［3］Dornfeld D，Min S，Takeuchi Y．Recent advances in mechanical micromachining［J］．Annals of the CIRP，2006，55:745－768．

［4］Quintana G，Ciurana J．Chatter in machining processes:a review［J］．International Journal of Machine Tools and Manufacture，2011，51:363－376．

［5］Zhang X J，Xiong C H．Milling stability analysis with simultaneously considering the structural mode coupling effect and regenerative effect［J］．International Journal of Machine Tools and Manufacture，2012，53:127－140．

［6］Salahshoor M，Ahmadian H．Continuous model for analytical prediction of chatter in milling［J］．International Journal of Machine Tools and Manufacture，2009，49:1136－1143．

［7］Huang C Y．Mechanistic modeling of process damping in peripheral milling［J］．Journal of Manufacturing Science and Engineering，2007，129:12－20．

［8］Altintas Y，Stepan G．Chatter stability of milling in frequency and discrete time domain［J］．Annals of the CIRP，2008，57（1）:35－44．

［9］Budak E，Ozlu E．Analytical modeling of chatter stability in turning and boring operations:a multi－ dimensional approach［J］．Annals of the CIRP，2007，56（1）:401－404．

［10］宋清华．高速铣削稳定性及加工精度研究［D］．济南:山东大学，2009．

［11］江浩．铣削加工振动主动控制［D］．上海:上海交通大学，2009．