延伸外摆线齿准双曲面齿轮建模与传动误差分析

刘 明

（贵阳铝镁设计研究院有限公司，贵州贵阳 550018）

螺旋锥齿轮是汽车、航空、工程机械和机床等机械产品中的关键零件［1］。目前，准双曲面齿轮主要分为弧齿、摆线齿和准渐开线齿制，美国格里森（Gleason）公司机床主要加工弧齿，瑞士的奥利康（Oerlikon）公司机床主要加工摆线齿，德国的克林贝格（Klingelnberg）公司机床主要加工摆线－准渐开线齿。其中我国引进最早的是格里森弧齿制，也是当前国内螺旋锥齿轮研究最多的［2－7］。由于摆线齿制采用连续分度法加工，提高了生产效率，这种齿制逐渐成为研究的热点［8－15］。国内外有许多学者对此进行了研究，多是考虑相互啮合的两个齿面，然而有些文献在实际建模的过程中没有详细的阐明及严格的验证［8－10，13－14］。现在格里森凤凰（PHOENIX®）II机床也逐渐加工摆线齿，但是摆线齿螺旋锥齿轮加工刀盘在自转的同时还绕摇台公转，故摆线齿螺旋锥齿轮比弧齿螺旋锥齿轮在理论研究上复杂。然而准双曲面齿轮又是螺旋锥齿轮中最复杂的一种，这给建立准双曲面齿轮几何模型增加了难度。本文针对延伸外摆线齿准双曲面齿轮进行研究，以格里森凤凰（PHOENIX®）II 600HC机床加工的摆线齿为研究对象，推导齿面方程及建立三维几何模型，并通过传动误差分析加以验证。

1 延伸外摆线齿锥齿轮铣齿加工原理

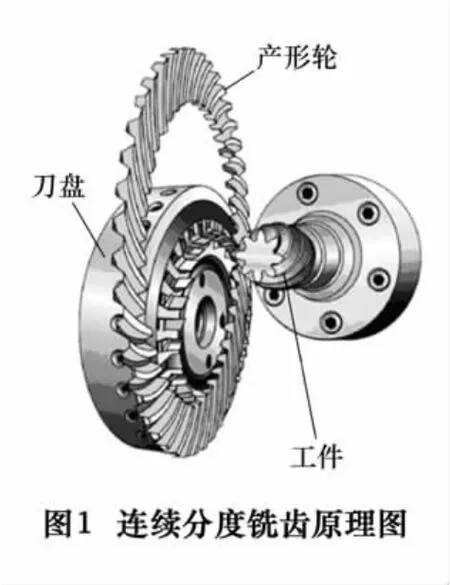
采用连续分度双面法铣齿，就是端铣刀盘上装有z0组刀齿，每组刀齿至少有外刀和内刀两个刀齿，分别加工齿的凹面和凸面。刀盘绕过一组刀齿时，轮坯转过一个齿，加工出齿槽的两面，如图1所示。无论是否有展成运动，都用连续分度双面铣齿方法，这种方法又称端面滚齿法，刀齿组z0相当于滚刀的头数。刀齿刀刃在齿槽空间的轨迹曲面构成产形轮，产形轮是为了研究方便假象的一个齿轮。

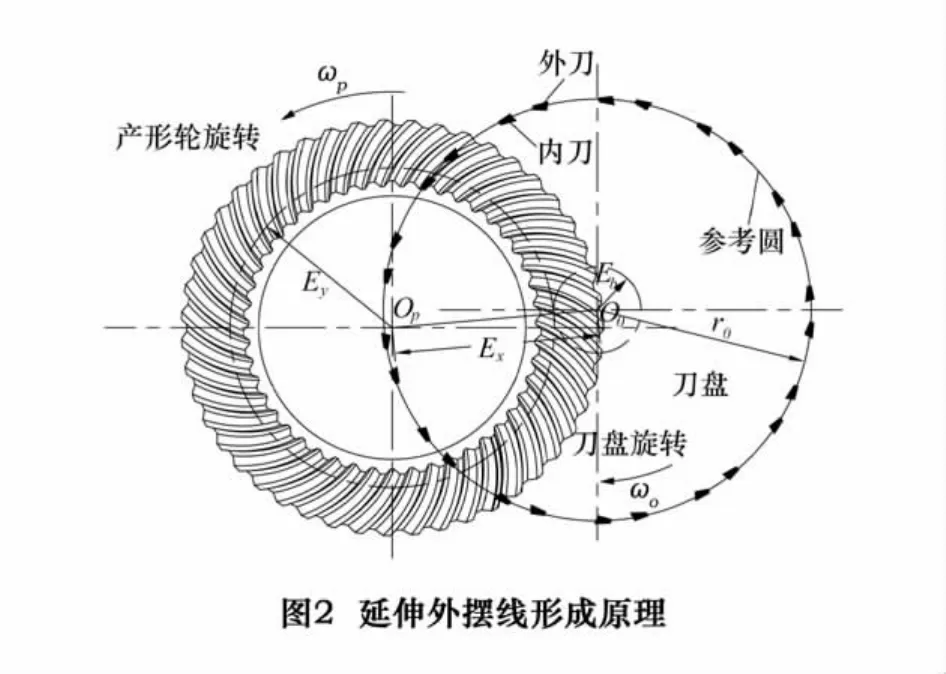
如图2所示，刀盘有z0组刀齿，轮坯齿数为zp，刀盘绕轴心O0自转，刀轴线则绕产形轮轴心Op公转，其转向与自转方向相同。刀盘与产形轮的相对运动可视为刀盘上半径为Eb的滚圆，在半径为Ey的产形轮基圆上作纯滚动［8］。点O0至点Op的距离称为径向刀位Ex，作为机床调整卡的已知量。对于刀盘和轮坯之间的相对运动，满足连续分度，用传动比Rb表示，即式（1），全文中下标i（i=1，2）分别表示小轮和大轮。

刀盘与产形轮之间满足如下关系;

式中:Ra为滚比［15］。

2 准双曲面齿轮齿面方程的推导

2．1 坐标变换

2．1．1 刀盘结构

为了便于精确逼近刀刃形状，而又不至于复杂，故将刀刃考虑成半径很大的圆弧，修根处暂不予考虑。图3为刀刃图，rb为刀刃圆弧半径;α为刀齿压力角，即坐标原点Ob的切线与Zb的夹角;hb为刀节点至刀尖的距离;u为刀齿节点P（Ob）沿刀刃向刀顶方向至任意一点的长度。在坐标系Sb下，有刀刃的数学表达式为

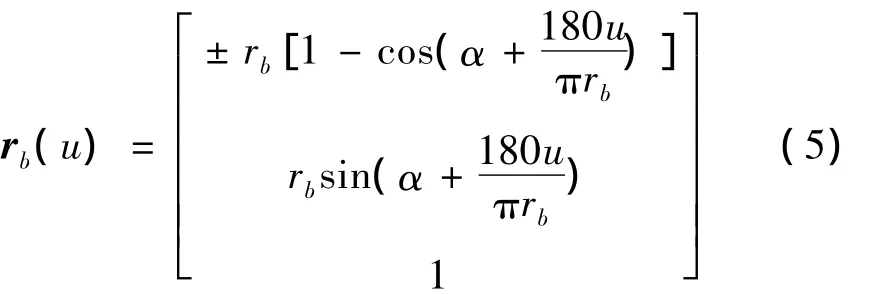
式中:“+”为外刀，“－”为内刀。

在图4中，坐标系Sb经过坐标变换到坐标系Sc，再由坐标系Sc变换到坐标系Sd，相应的变换矩阵为Mcb和 Mdc，详见式（6）、（7）。

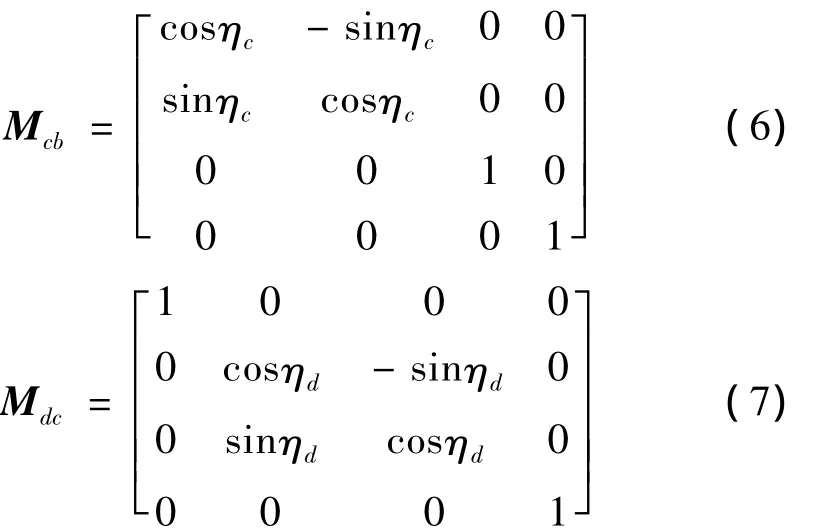
对于加工旋向不同的齿轮，选用的刀盘不同，刀盘回转的方向也不同。图5为加工左旋齿轮的TRI－AC刀盘示意图，刀齿按照内刀、外刀的顺序顺时针排列，刀盘顺时针回转;图6为加工右旋齿轮的TRI－AC刀盘示意图，刀齿按照内刀、外刀的顺序逆时针排列，刀盘逆时针回转。左右刀盘形成镜像的关系，以过刀齿节点P且垂直于刀盘轴线的平面作为XY平面，建立图5和6的坐标系。图中r0为刀盘名义半径，刀齿节点P为坐标系Sd原点Od，Se为随刀盘旋转的坐标系，坐标原点Oe和坐标原点Of重合，ε为刀齿方向角，θ为刀盘的转角。坐标系Sd到Se，再到Sf的变换矩阵分别为 Med和Mfe，详见式（8）、（9），“+”为加工左旋，“－ ”为加工右旋。最后得到刀刃在坐标系Sf下的数学表达式 rf（u，θ），见式（10），式中含有两个参变量u、θ。

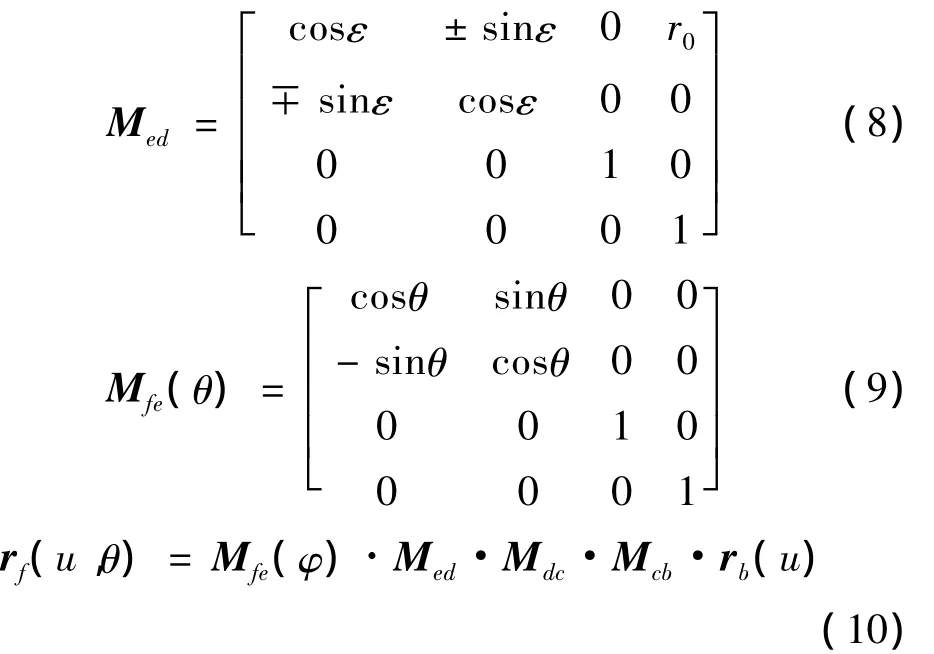
2．1．2 机床运动模型

如图7所示为延伸外摆线铣削机床运动模型。

根据本文的研究内容为半展成法加工，小轮展成法加工，大轮成形法加工。下面分别进行讨论。

（1）展成法加工的机床运动变换

图8为刀倾结构，经过坐标系Sf到Sj的变换得到变换矩阵Mjf，见式（11）所示，i为刀倾角。图9所示，坐标系Sm固结于摇台上，随摇台一起作展成运动，坐标系Sk相对于坐标系Sm静止，q0为角向刀位初始值，Ex为径向刀位值，j为刀转角。坐标系Sj到Sk，再到Sm的变换矩阵分别为Mkj和Mmk，见式（12）、（13）。

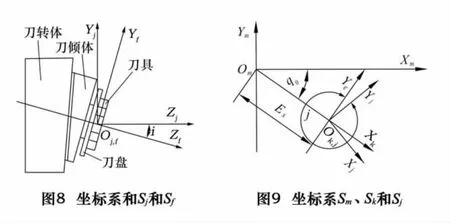
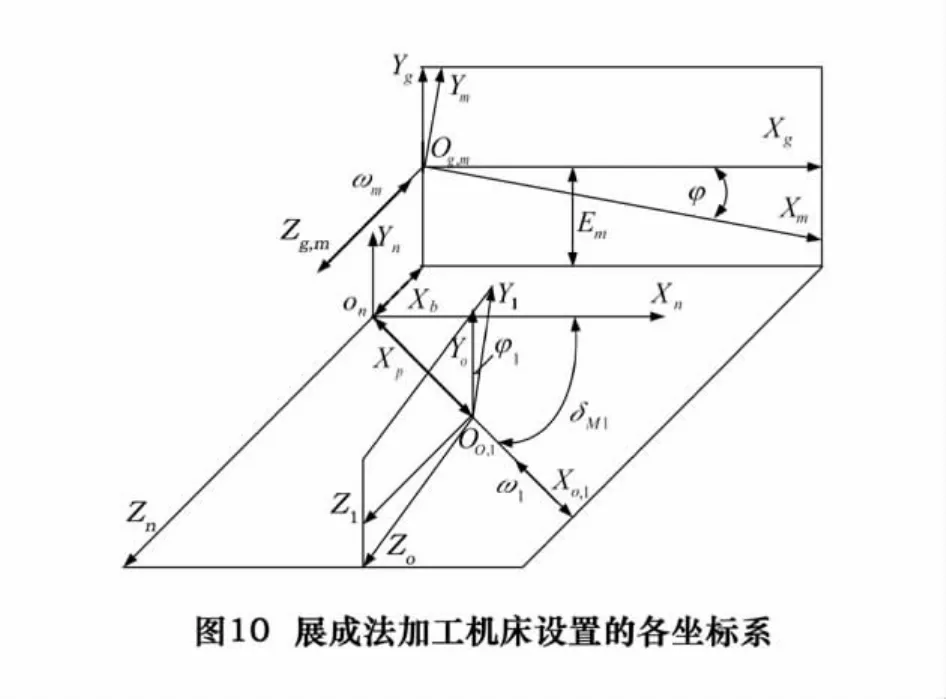
图10所示，Sg为机床坐标系，绝对静止，初始时坐标系Sm与Sg重合，此后摇台作角速度为ωm的展成运动，任意时刻的转动角度为参变量φ，工件作角速度为ω1的旋转运动，任意时刻的转动角度为φ1，根据连续分度展成原理有φ1=Rbθ+Raφ。经过一系列坐标变换得到式（14）～（17）的变换矩阵。

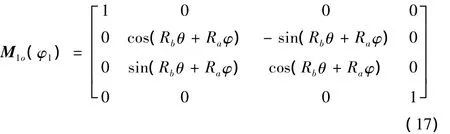
（2）成形法加工的机床运动变换

对于成形法加工，没有展成运动，没有刀倾和刀转，也没有垂直轮位和床位，整个坐标系得到简化，如图11所示。坐标系Sm固结于机床床身，静止不动;坐标系Sk固结于刀盘上，随刀盘一起转动;坐标系Sl、So相对于Sm静止;坐标系S2随工件一起作旋转运动，角速度为ω2，任意时刻的转动角度为φ2，根据连续分度展成原理有φ2=Rbθ。H2为水平刀位，V2为垂直刀位，δM2为安装角。经过一系列坐标变换得到式（18）～（20）的变换矩阵。

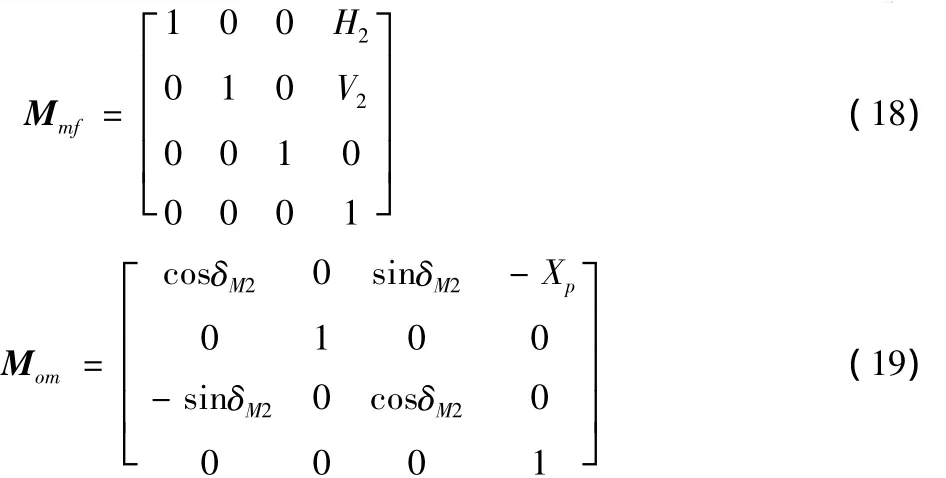
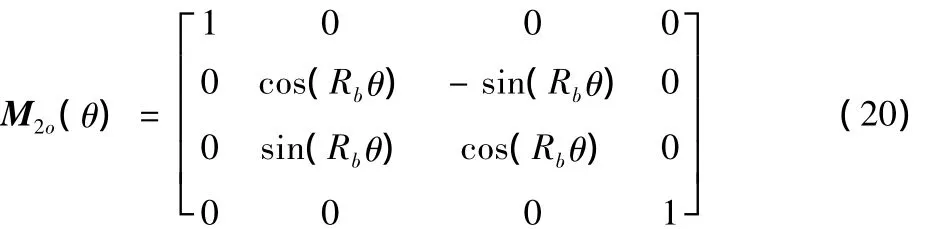
2．2 齿面方程

本文以小轮左旋，展成法加工，大轮右旋，成形法加工为研究对象。将rf（u，θ）分别转化到坐标系S1和S2里面得小轮和大轮的齿面方程，见式（21）、（22）。从式中可以看出展成法加工的齿面含有u、θ、φ三个未知数，而成形法加工的齿面含有u、θ两个未知数。

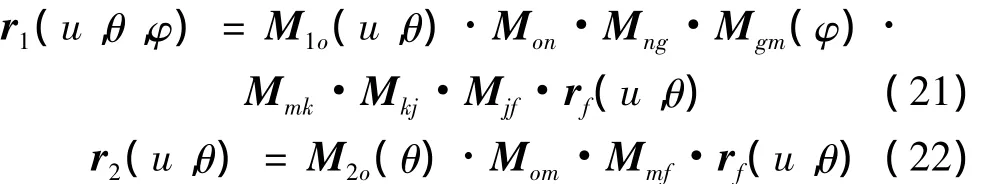
对应的单位法向量为

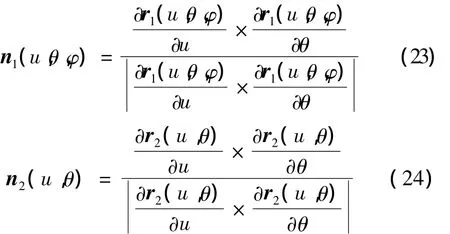
对于展成法，由齿轮啮合理论得到啮合方程［7］。

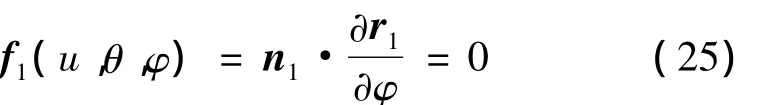
3 几何模型的建立

由于展成法齿面方程含有3个未知数，除了啮合方程外，还要有2个方程才能求解;成形法齿面方程含有2个未知数，也需要2个方程才能求解，因此借助齿面的边界来求解。过齿轮轴截面做旋转投影面，如图12所示，对齿面进行网格规划［12］。为了便于理解和求解，先在坐标系Sh（oh，xh，yh）下求解，xh过分锥母线，坐标原点oh，1为轮坯锥顶点。

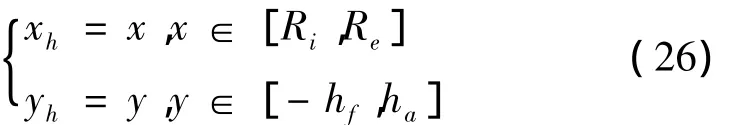
式中:Ri、Re、hf和ha分别为轮坯小端锥距、大端锥距、齿根高和齿顶高。通过坐标变换由Sh到S1得

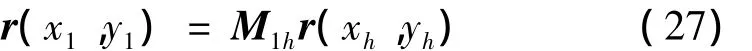
以一对格里森机床加工的延伸外摆线齿准双曲面齿轮为例，相关参数值见表1，根据上述推导出的理论齿面，联立式（21）、（25）和（27）得式（28）;联立式（22）、（27），得式（29）。

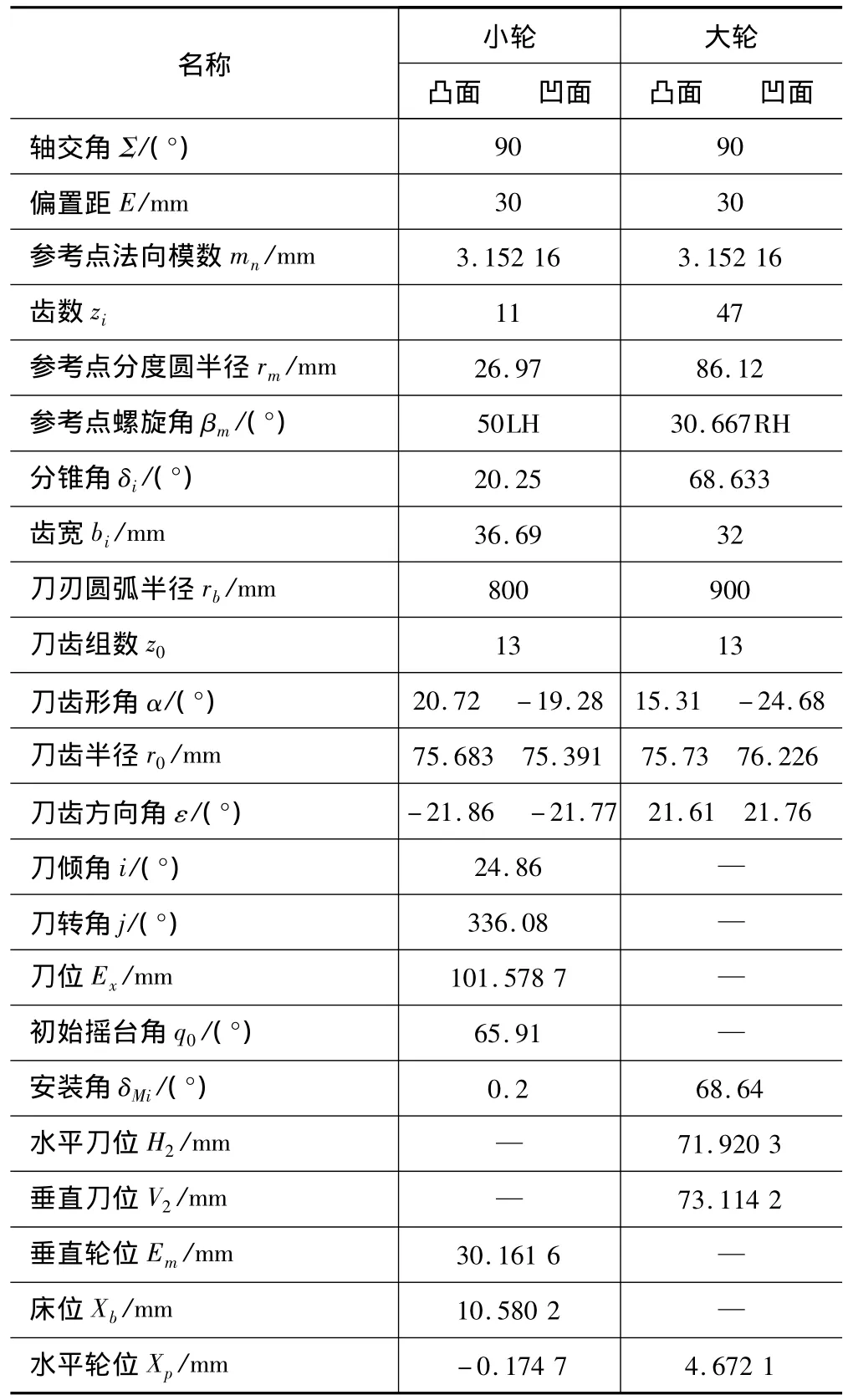
表1 延伸外摆线准双曲面齿轮副基本参数与加工参数

（1）展成法小轮

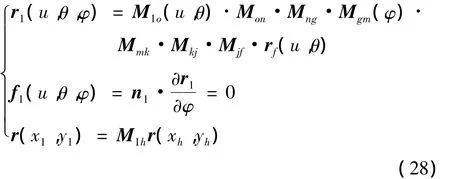
（2）成形法大轮

通过齿面离散求解非线性方程组，得到齿面相应的坐标值。运用Matlab7．0软件计算出各个坐标值，导入三维软件Pro/E，由点到线、线到面、面到体的过程建立三维模型［5］，如图13齿轮三维几何模型。

4 传动误差的分析

图14为延伸外摆线准双曲面齿轮的传动装配图，借助多体动力仿真软件ADAMS进行接触传动误差的分析。相应的参数设置如下:当小轮驱动大轮时，小轮输入轴转速n1=900（°）/s，T1=240 N·m，则大轮的负载转矩为T2=T1z2/z1=1 025 N·m，理论输出转速n2=n1z1/z2=210.638（°）/s;当大轮驱动小轮时，大轮输入轴转速n2=211（°）/s，T2=1 025 N·m，则小轮的负载转矩为T1=T2z1/z2=240 N·m，理论输出转速n1=n2z2/z1=901.545（°）/s。考虑润滑条件下，定义静摩擦因数为0.08，动摩擦因数为0.05。

4．1 小轮凹面驱动大轮凸面的传动误差

小轮驱动大轮，小轮凹面和大轮凸面为工作齿面，其传动误差如图15a所示，平均角速度210.394 2（°）/s，最大角速度为 232.643 5（°）/s，最小角速度为180.283 8（°）/s。平均角速度与理论值相比较，其传动误差为－0.243 8°，相对误差0.12%。

4．2 小轮凸面驱动大轮凹面的传动误差

小轮驱动大轮，小轮凸面和大轮凹面为工作齿面，其传动误差如图15b所示，平均角速度210.445 6（°）/s，最大角速度为 231.759 2（°）/s，最小角速度为187.718（°）/s。平均角速度与理论值相比较，其传动误差为－0.192 4°，相对误差0.09%。

4．3 大轮凹面驱动小轮凸面的传动误差

大轮驱动小轮，大轮凹面和小轮凸面为工作齿面，其传动误差如图15c所示，平均角速度901.259 6（°）/s，最大角速度为 1 197.257 2（°）/s，最小角速度为624.628 5（°）/s。平均角速度与理论值相比较，其传动误差为－0.285 4°，相对误差0.03%。

4．4 大轮凸面驱动小轮凹面的传动误差

大轮驱动小轮，大轮凸面和小轮凹面为工作齿面，其传动误差如图15d所示，平均角速度901.324 6（°）/s，最大角速度为 1 058.524 5（°）/s，最小角速度为720.200 4（°）/s。平均角速度与理论值相比较，其传动误差为－0.220 4°，相对误差0.02%。

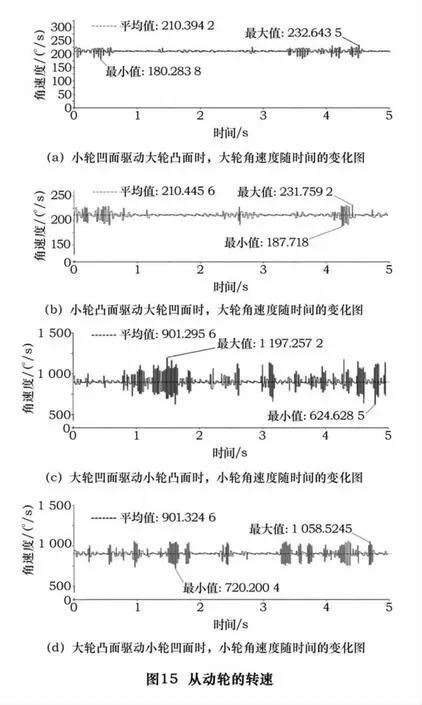
总之，从图15来看，齿轮传动输出角速度曲线在平均值上下波动，虽然传动误差相差不大，但是从4幅图可以看出c、d两图的剧烈程度较大，波动比较激烈。这符合选择小轮为驱动轮的工程运用，同时也验证了模型的正确性。

5 结语

（1）根据刀盘、被加轮坯和摇台在加工中的相对运动和位置关系建立了切齿啮合的数学模型，根据空间啮合原理和切齿啮合关系，由矩阵法推导了被加工齿轮的齿面方程。

（2）结合一实际例子，由齿面网格划分，在Matlab中求解齿面方程，计算得到齿面离散数据，在Pro/E中读取数据并建立了相对精确的延伸外摆线齿准双曲面齿轮三维模型。

（3）通过ADAMS进行动力学仿真，得到了准双曲面齿轮在各种驱动方式下的传动误差，其从动轮的角速度与理论计算的角速度相接近，误差在允许的范围。当小轮作为主动轮时传动性能相对较好，相对传动误差低于0.2%，符合工程中选择小轮为主动轮的实际情况，验证了三维模型的准确性。正确模型的建立，为延伸外摆线齿准双曲面齿轮的优化设计、制造和分析检验打下了基础。

［1］马伟，邓效忠，曹雪梅，等．高齿弧齿锥齿轮的承载啮合仿真和动态性能试验［J］．中国机械工程，2004，15（11）:951－953．

［2］Chen Shu－han，Yan Hong－zhi，Ming Xing－zu．Analysis and modeling of error of spiral bevel gear grinder based on multi－body system theory［J］．Journal of Central South University of Technology，2008，15（5）:706－711．

［3］唐进元，蒲太平，戴进．SGM法加工的螺旋锥齿轮几何建模研究［J］．机械传动，2008，32（1）:43－46．

［4］杨小辉，方宗德，杨青．UG环境下利用GRIP实现螺旋锥齿轮数值仿真齿面的精确重建［J］．机床与液压，2005（1）:162－164．

［5］唐进元，黄云飞，周超，等．弧齿锥齿轮展成齿面的几何建模［J］．计算机仿真，2009，26（2）:293－297．

［6］陈书涵，严宏志，明兴祖，等．螺旋锥齿轮误差齿面及差曲面的建立与分析［J］．中国机械工程，2008，19（18）:2156－2161．

［7］Litvin Faydor L，Fuentes Alfonso，Fan Qi，et al．Computerized design，simulation of meshing，and contact and stress analysis of face－milled formate generated spiral bevel gears［J］．Mechanism and Machine Theory，2002，37（5）:441－459．

［8］董学朱．摆线齿锥齿轮及准双曲面齿轮设计和制造［M］．北京:机械工业出版社，2002．

［9］吴联银，魏洪钦，王小椿．Free－form型机床展成延伸外摆线锥齿轮的齿面几何研究［J］．西安交通大学学报，2001，35（3）:322－325．

［10］Yi－ Pei，Fong Zhang－ Hua，Lin Grandle C Y．Mathematical model for a universal face hobbing hypoid gear generato［J］．Journal of Mechanical Design，Transactions of the ASME，2007，129（1）:38－47．

［11］John Argyris，Alfonso Fuentes，Litvin Faydor L．Computerized integrated approach for design and stress analysis of spiral bevel gears［J］．Computer Methods in Applied Mechanics and Engineering，2002，191（1）:1057－1095．

［12］聂少武，邓效忠，李天兴．奥利康准双曲面齿轮的理论齿面推导及仿真［J］．机械传动，2009，33（2）:20－22．

［13］Yi－ Pei，Fong Zhang－ Hua．Flank modification methodology for face－ hobbing hypoid gears based on ease－ off topography［J］．Journal of Mechanical Design，Transactions of the ASME，2007，129（3）:1294－1302．

［14］李巍，李剑锋，王青云．克林贝格摆线齿锥齿轮齿面方程及图形仿真［J］．机械科学与技术，2006，25（12）:1462－1466．

［15］Vimercati M．Mathematical model for tooth surfaces representation of face－hobbed hypoid gears and its application to contact analysis and stress calculation［J］．Mechanism and Machine Theory，2007，42（6）:668－690．