基于贝叶斯网络的电抗器健康诊断

赵文清 ，王 强 ，牛东晓

（1.华北电力大学 控制与计算机工程学院，河北 保定 071003；2.华北电力大学 经济与管理学院，北京 102206）

0 引言

随着电网现代化程度的不断提高，以及建设“统一坚强”智能电网目标的提出，电气设备从事后检修到计划检修，再到状态检修的转变是技术发展的必然趋势［1-2］。并联电抗器是高电压、远距离交流输电网络中不可缺少的重要设备，它可以改善沿线工频电压分布，增强系统稳定性及送电能力；降低工频暂态过电压，并进而限制操作过电压的幅值；改善轻载线路中的无功分布，降低有功损耗，提高送电效率等，因此，其运行状态关系到整个电力系统的安全稳定运行。

电抗器的健康诊断是电抗器状态检修的基础，目前针对电抗器的诊断都是以油中溶解气体分析（DGA）为主的方法，有传统的色谱分析法［3］、比值法［4］，也有基于人工智能的模糊数学［5］、神经网络［6］等。文献［4］提出了基于三比值法的电抗器故障诊断，该方法虽然实现简单，但准确性不高，具有片面性。文献［5］提出了一种模糊逻辑模型来分析油中溶解气体，其能提供以DGA数据为基础的设备排名，但不能评估设备运行状态。鉴于此，本文充分考虑电抗器研发技术的难题和运行期间出现的主要问题，并综合电抗器的历史、当前和未来状态，建立了基于贝叶斯网络的电抗器健康诊断模型，为电抗器由定期预防性维修向状态维修的过渡提供技术支持。

1 电抗器状态量和评分方案的确定

并联电抗器的绝缘结构包括主、纵绝缘结构［7］，主绝缘结构由油和纸板构成，利用纸筒合理分割油隙，配置符合电场等位线形状的角环，并放置在最佳位置上。纵绝缘结构中，首端柱线圈采用全纠结结构，末端柱线圈采用纠结连续式结构，通过多根并联导线间的交错插花增大线圈纵向电容。随着电抗器容量的增大，复杂的内部结构引起的磁场分布更复杂，漏磁更大。研究表明电抗器治理的难点在于局部过热，其主要由漏磁引起。铁芯饼与间隙材料构成铁芯柱，磁致伸缩和铁芯间的电磁力引起振动产生噪声。绝缘、局部过热、振动和噪声是困扰电抗器技术发展的难题［8-9］，用它们来评估电抗器的健康状态最有说服力。本文针对这些问题，对电抗器的健康状态进行全面评估，采用表1所示方案诊断电抗器健康状态。

表1 电抗器健康状态评分Tab.1 Scores of reactor health statuses

2 电抗器分层评分模型

综合考虑试验数据的量值和变化量来对试验项目进行评分。规定当数据向有利方向变化时变化量得分为满分，反之，用评分模型和阈值来进行评分。

2.1 评分模型的确定

本文采用半梯模型进行电抗器状态信息评分。最常见的半梯模型有升半梯模型和降半梯模型，对于数值越大越好的指标，采用升半梯模型；反之采用降半梯模型。为方便计算，将分值归一化，即评分模型计算结果为0～1之间（对应于0～100分）。

升半梯模型和降半梯模型的表达式分别如式（1）和式（2）所示：

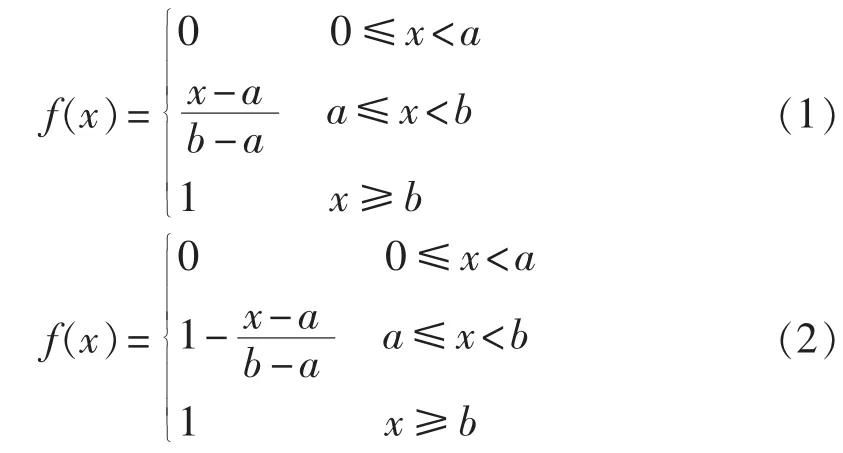
其中，a和b为阈值，x为评分参数。

2.2 评分阈值的确定

根据电力设备预防性试验规程以及现场调研资料［10-14］，本文所采用的试验参数对应的评分模型和模型阈值见表2—4。

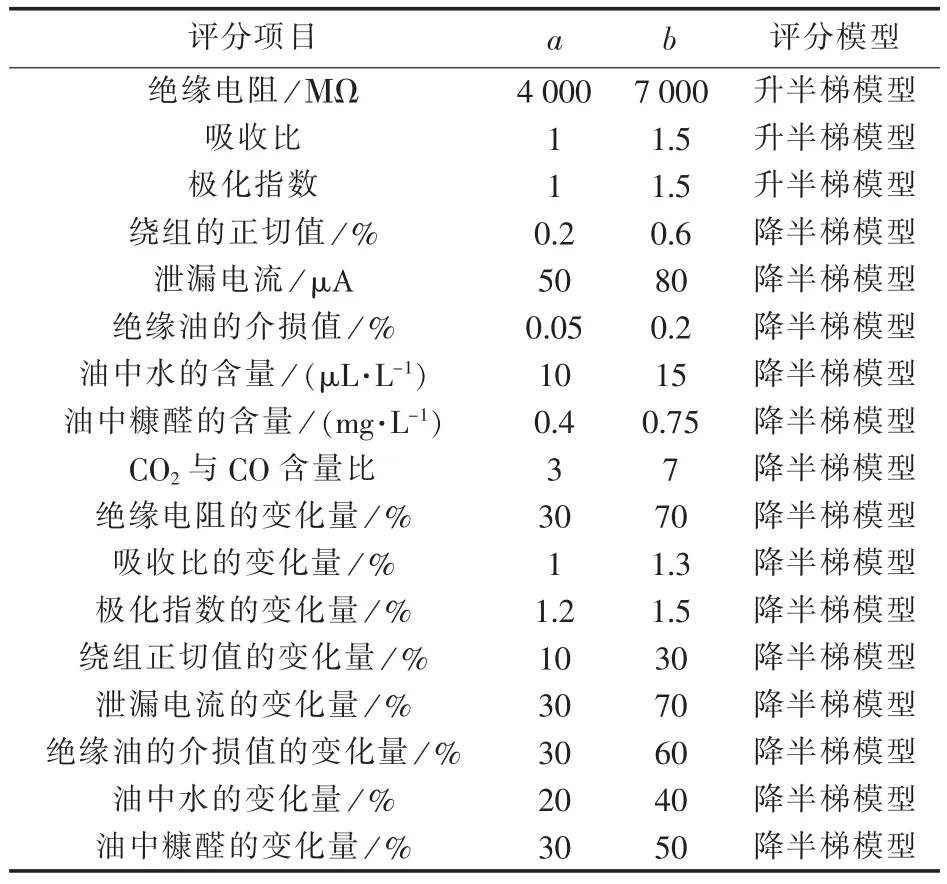
表2 电抗器绝缘问题的评分模型和阈值Tab.2 Scoring model and threshold value of reactor insulation evaluation

表3 局部过热问题的评分模型和阈值Tab.3 Scoring model and threshold value of reactor local overheating evaluation

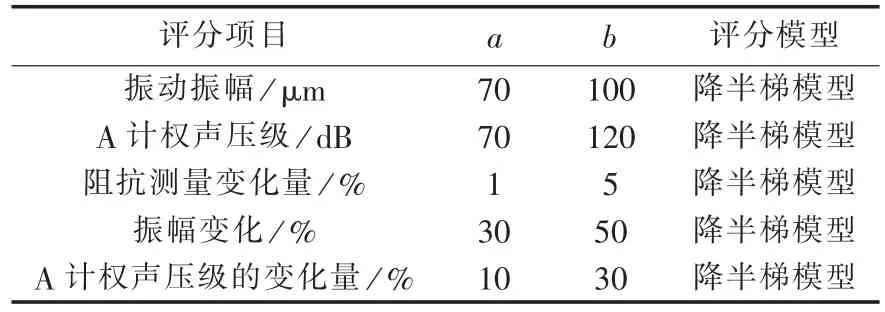
表4 振动和噪声问题的评分模型和阈值Tab.4 Scoring model and threshold value of reactor vibration&noise evaluation

2.3 分层评估模型

图1所示为电抗器健康状态分层评估模型。图中，油中糠醛、油中微水、CO2与CO含量比为绝缘老化的3个并列子层，绝缘老化和绝缘受潮为绝缘问题的2个并列子层，依此类推，图1可直观地反映这种层次关系。图中每层的得分都是由该层的子层得分综合得出，计算原则是：若子层各项得分均≥0.7（得分归一化后），则取各项得分的算术平均值为父层的得分；反之父层得分为子层各项得分的最小值。利用这些得分逐层计算，就可得到电抗器的健康状态。

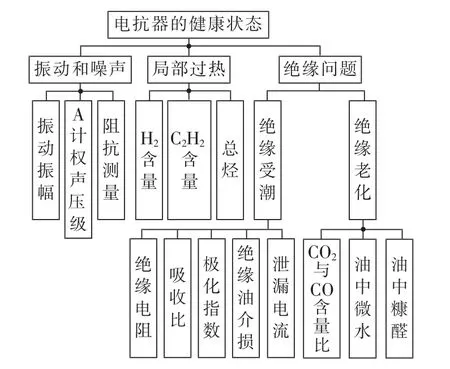
图1 分层电抗器健康状态评估模型Fig.1 Layered reactor health diagnosis model

3 基于贝叶斯网络的电抗器综合健康状态诊断

3.1 基本思想

2.3 节模型通过分析近期的预防性试验数据来确定电抗器的运行状态。而实际上，电抗器当前状态往往受其历史状况的影响。此外，电抗器状态评估的目的是为确定维修策略提供依据。若下一个维修周期中电抗器将出现故障，则需要缩短检修周期，提前安排检修；若下一个维修周期中电抗器状态非常好，不会出现故障或异常，则说明电抗器的各项状态信息劣化缓慢，可适当延长检修周期。因此，仅分析近期试验数据往往难以准确获得电抗器的综合状态，应综合考虑电抗器的历史、当前和未来状态。

灰色系统［16］是邓聚龙教授于20世纪80年代初创立的新兴横断学科，它适用于对时间序列短、统计数据少、信息不完全系统的建模与分析。对电抗器而言，电抗器的历史、当前参数已知，但影响电抗器状态的其他因素，如天气情况等难以确定，故电抗器的状态是灰色的。本文提出了无偏灰色模型，通过对电抗器预防性试验数据的处理和灰色模型的建立，根据电抗器试验参数的发展规律，对电抗器的未来状态作出科学的定量预测。贝叶斯网络［17］是一种基于网络结构的有向图解描述，它被认为是目前不确定知识表达和推理领域最有效的理论模型，能发现大量变量之间的关系，是进行数据预测、分类的有力工具。

根据以上分析，本文提出了基于贝叶斯网络的电抗器综合健康状态的诊断方法，该方法首先对电抗器的各类状态信息进行预测，得到未来时间段的相关参数数据；然后分别对历史、当前和未来试验数据按照分层评估模型来评分，得到电抗器的历史、当前和预测健康状态；最后，通过贝叶斯网络综合历史、当前和预测状态得到电抗器的综合状态。

3.2 诊断模型

为诊断电抗器的综合状态，本文提出了基于贝叶斯网络的电抗器健康诊断模型，如图2所示。该模型最底层为电抗器的综合健康状态，该节点具有5个状态（详见表1）。基于贝叶斯网络的电抗器健康诊断模型立足于电抗器的研发技术难题和实际运行中的常见问题，充分利用各项预防性试验数据及其变化量对电抗器状态的影响，综合考虑了电抗器历史、当前和未来状态，最终得到电抗器的健康状态。

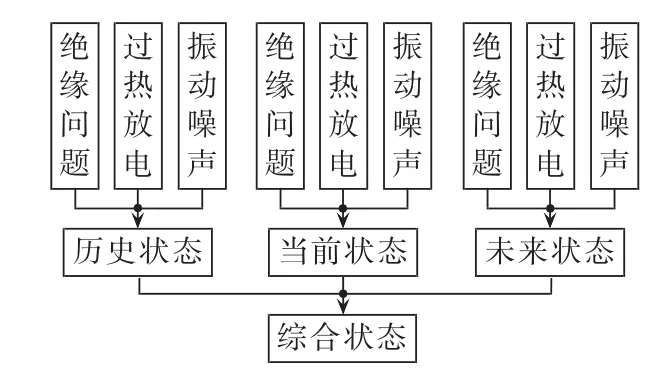
图2 基于贝叶斯网络的电抗器健康诊断模型Fig.2 Reactor health diagnosis model based on Bayesian network

3.3 电抗器健康诊断模型条件概率表的确定

贝叶斯网络条件概率表的学习方法可分为基于经典统计学的学习方法和基于贝叶斯统计学的学习方法两大类。前者具有理论成熟、计算简单的优点，但它只利用了实例数据集所提供的信息，无法加入专家的知识，所以对实例数据集的依赖性大；后者有机地综合了实例数据和专家知识这2类信息，因此对实例数据集的依赖性较低，其学习结果更精确。本文采用前者计算贝叶斯网络模型条件概率［15］。

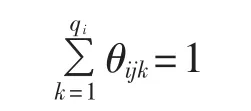
由条件期望估计法可知，贝叶斯网络条件概率表的学习公式为：

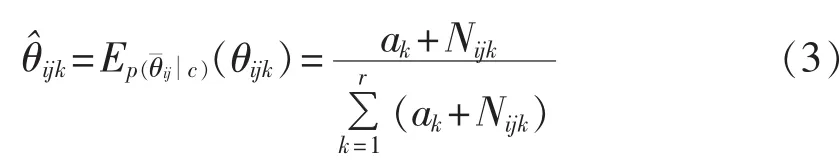
3.4 实例分析

本文收集了晋东南某变电站的电抗器试验数据、DGA数据和电抗器的运行工况，根据图1给出的分层模型对其当前状态和历史状态进行打分，用无偏灰色模型对其未来状态进行预测并进行打分，给出其综合状态。这些评分和电抗器的运行状态构成了电抗器的贝叶斯网络健康诊断模型的训练样本。样本综合状态统计信息见表5。

表5 样本统计信息Tab.5 Statistic information of sample

举例说明条件概率表的计算：当父节点组合为“历史状态=A，当前状态=A，未来状态=A”时，计算出综合状态分别取A、B、C、D、E时的条件概率。先统计满父节点组合下综合状态为A、B、C、D、E时的样本个数为 80、9、0、0、0，由式（3）可算出各条件概率值：

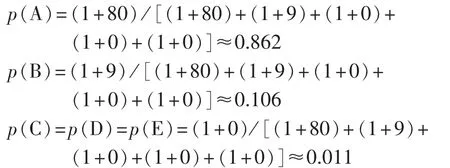
限于篇幅，本文只列出部分条件概率表，见表6。

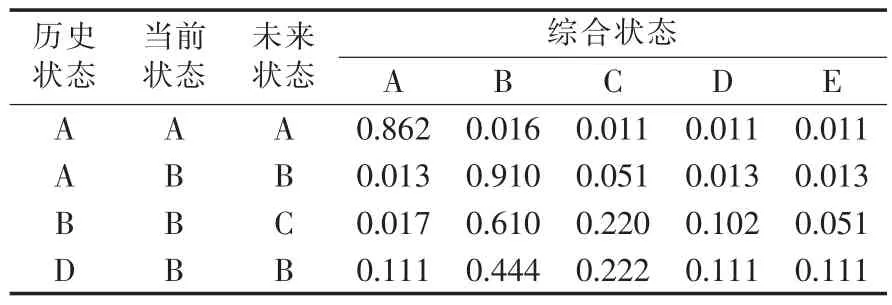
表6 综合状态条件概率Tab.6 Comprehensive conditional probability

实例分析证明，本文提出的基于贝叶斯网络的电抗器健康诊断方法，采用5级状态评定法，能够更准确地描述电抗器的健康状态。

4 结语

本文综合考虑电抗器的研发技术难题和运行期间出现的常见问题，充分考虑各项预防性试验的重要性和参数变化对电抗器状态的影响，用分层评分模型给出电抗器的综合评分，试验证明该方法合理、高效。为全面把握电抗器的健康状态，提出无偏灰色预测模型，对电抗器的未来状态进行了预测。最后，提出贝叶斯网络健康诊断模型，综合考虑了电抗器历史、当前和未来状态，给出电抗器的综合健康状态。本文所提模型能够高效地掌握电抗器运行期间的健康状态，以实现电网的可靠、经济、高效、环境友好和使用安全为目标，推动了“坚强”智能电网的建设。