基于频率特征的失步解列判据原理
吴麟琳,黄少锋
(华北电力大学 四方研究所,北京 102206)
0 引言
我国电网已进入了大容量、远距离、多区域互联的发展时期,西电东送、南北互联在带来巨大经济效益的同时使电网日趋复杂化,系统失步发生的概率也大幅增加[1-3]。失步解列作为防止系统崩溃的最后一道防线,对电力系统安全稳定运行具有重要意义[4-5]。目前基于视在阻抗轨迹的解列判据整定较为困难,容易受到系统运行方式和网络结构变化的影响;根据基于ucos φ轨迹的失步解列判据能够得到失步中心出现的时刻,却难以得到失步中心的位置;基于相角的失步解列判据在电网复杂的情况下,电网潮流方向改变时会造成误判;基于补偿原理的失步解列判据在线路带大量中间负荷时难以实现[6-8]。
本文研究了电力系统失步振荡过程中,两侧电动势幅值相等及不等情况下电压频率的特征,从而提出一种基于频率特征的失步解列判据,该判据可以区分同步振荡和失步振荡,识别振荡中心的位置,同时不受系统结构变化和运行方式变化的影响。目前对电网频率测量算法的研究[9-11]和PMU在频率测量方面的应用[12-13]为判据的实现奠定了理论基础。
1 失步振荡时电压频率的特征
在图1所示的MN线路等值系统中,两侧等值电动势分别为 ES、ER,其等值正序阻抗为 ZS、ZR;两侧母线电压为UM、UN;线路正序阻抗为ZMN;M侧流向N侧的线路电流为IM,N侧流向M侧的线路电流为 IN。
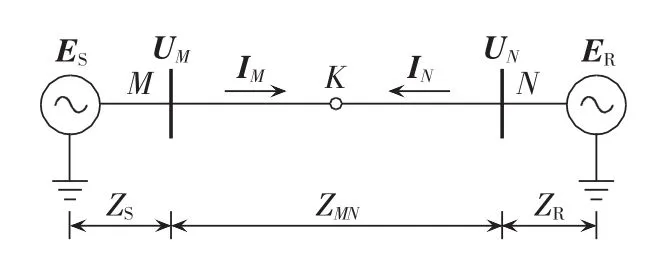
图1 MN线路等值系统图Fig.1 Equivalent network of line MN
当系统发生失步振荡时,不妨设M侧是送电端,ES超前于 ER,ES=ERejδ,其角速度可分别表示为 ωS=ω+Δω 与 ωR=ω;ES与 ER之间的夹角 δ在 0°~360°的范围内周期性变化。不妨设t=0时ES与ER的相量关系如图2所示。其中δ0为t=0时ES与ER之间的夹角,则有:

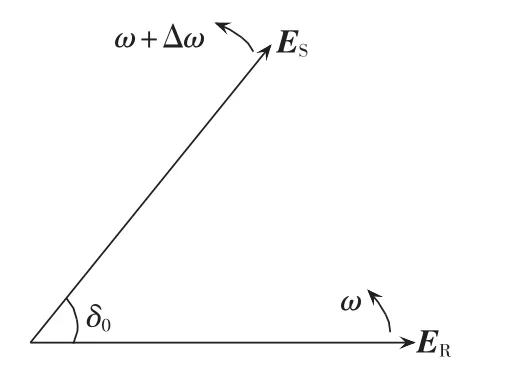
图2 t=0时刻ES与ER的相量关系图Fig.2 Phasor diagram of ESand ERat t=0
如图1所示,计及K点的电气位置系数可以表示为:

其中,0<ρK<1。母线M和母线N处的电气位置系数可分别表示为和,则线路上任意K点的电压可以表示为:
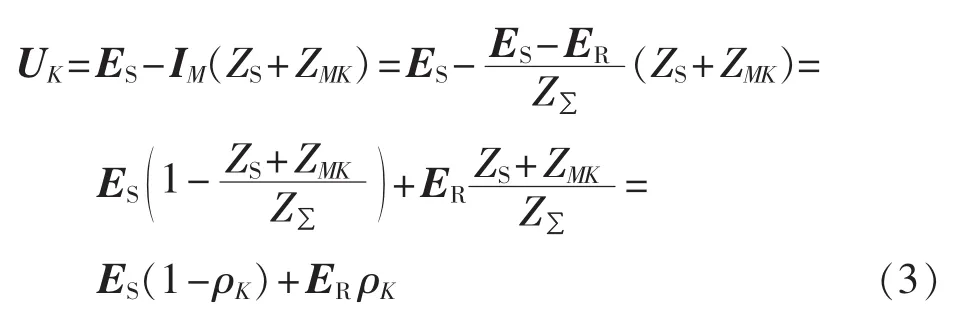
由式(3)可求得K点电压的幅值:

1.1 失步振荡中心的电压频率特征
在两侧电动势幅值相等且系统中各元件阻抗角相等的情况下,振荡中心位于整个电气的中心,即ρK=1/2 处[14]。 从而由式(4)可以求得振荡中心的电压幅值:

由式(3)和式(5)得到振荡中心电压的瞬时值为:
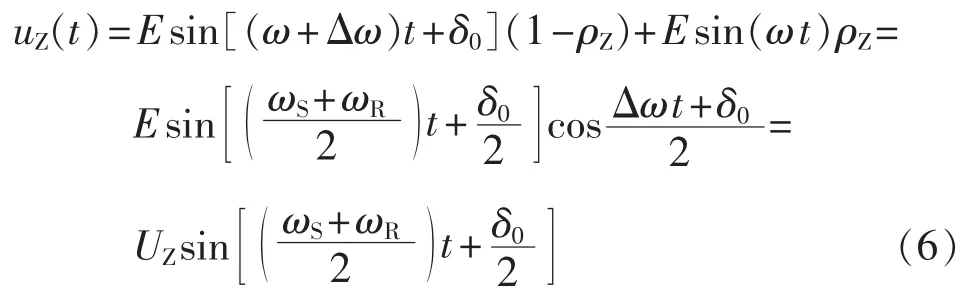
设fS和fR分别为两侧等值电动势的频率,则振荡中心的电压角速度为(ωS+ωR)/2,其频率为(fS+fR)/2。根据文献[5]的研究,电流IM在系统振荡时的频率也为(fS+fR)/2,即振荡中心处的电压频率和电流频率相等。
1.2 失步振荡时任意K点电压频率特征
在系统失步振荡情况下,当 0°<δ<180°时,根据式(3)能够得到如图3所示的相量关系图。

图3 ES、ER和UK的相量关系图Fig.3 Phasor diagram of ES,ERand UK
图中ω+ΔωK为线路上任意K点电压相量的角速度,由于夹角δ呈周期性变化,因此不妨设t=0时ES与 ER之间的夹角 δ0=0,相量 UK和 ρKER之间的夹角δK0=0,从而可以得到:
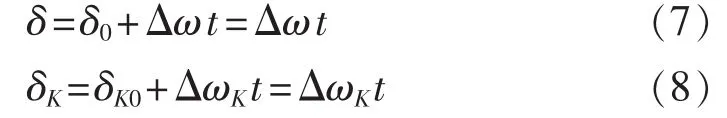
利用平行四边形法则和余弦定理可以得到:
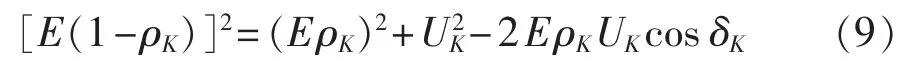
由式(7)—(9)可以得到 δK的表达式:
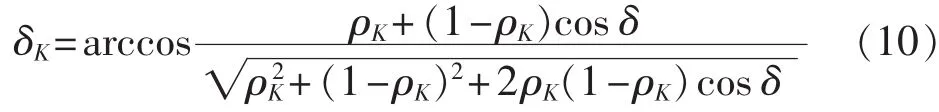
从而可以得到,当 0°<δ<180°时,线路上任意K点对应的电压相量UK的频率为:
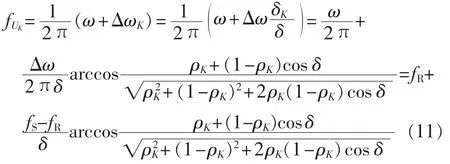
同理,当 180°<δ<360°时,利用平行四边形法则和余弦定理能够得到K点对应的电压相量的频率为:
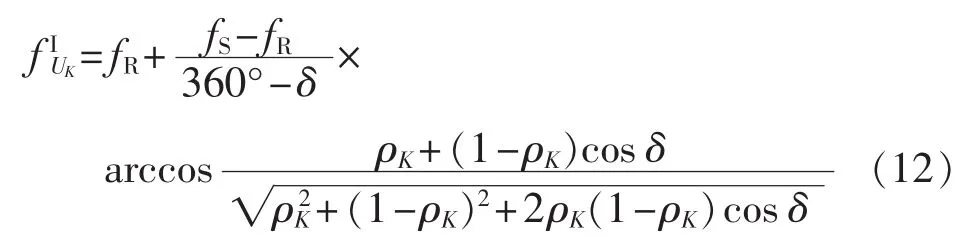
可以看出线路上任意K点对应的电压相量UK的频率fK取决于K点的电气位置系数、系统两端等值电动势的频率及其夹角δ。由于前文所设,M侧是送电端,ES超前于 ER,即ES的频率fS大于 ER的频率 fR,由式(11)和式(12)可以得到 K点电压频率的变化规律如图4所示。
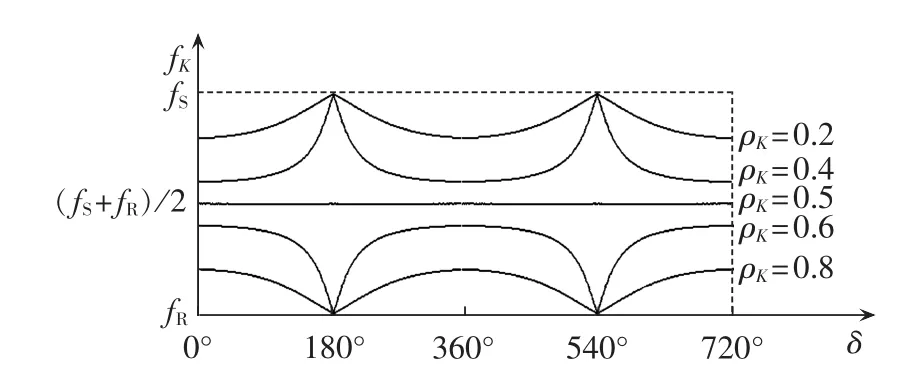
图4 K点电压频率图Fig.4 Voltage frequency waveforms of node K
图4为2个失步振荡周期内电压频率的变化规律,可见电压频率随两侧电动势夹角连续变化,失步振荡中心即ρK=1/2处的电压频率等于(fS+fR)/2,其一侧的电压频率在(fS+fR)/2~fS之间周期性变化,另一侧的电压频率在fR~(fS+fR)/2之间周期性变化。
2 两侧电动势幅值不等时电压频率的特征

当0°<δ<180°时,其相量关系仍如图3所示,利用余弦定理和平行四边形法则可以得到:
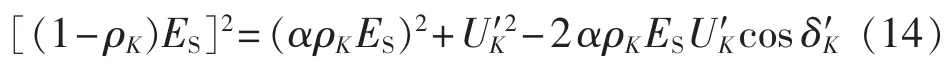
其中,δ′K为两侧电动势幅值不等时,UK与 ρKER之间的夹角。 由式(13)和式(14)可以得到 δ′K的表达式:

当 0°<δ<180°时,由式(7)、式(8)和式(15)可以得到线路上任意K点对应的电压相量的频率为:

同理,当 180°<δ<360°时,再次利用余弦定理和平行四边形法则可以得到线路上任意K点对应的电压相量的频率为:

在两侧等值电动势幅值不等的情况下,当系统发生失步振荡时,根据式(16)和式(17)可以得到如图5所示的线路上任意K点的电压频率变化规律。
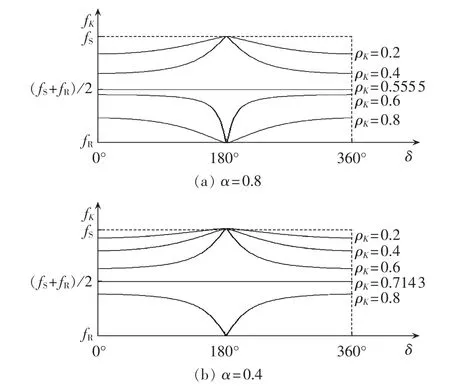
图5 两侧电动势幅值不等时K点电压频率图Fig.5 Voltage frequency waveforms of node K when electromotive force amplitude of one side is unequal to that of the other side
图5为一个失步振荡周期内电压频率的变化规律,可见当α=0.8时,振荡中心的电气位置系数ρK=0.5555;当α=0.4时,振荡中心的电气位置系数ρK=0.7143。可见两侧电动势幅值差别越大,振荡中心越靠近幅值较小的一侧。与两侧电动势幅值相等的情况相比较,线路上任意一点电压频率仍具有如下规律:失步振荡中心处的电压频率等于(fS+fR)/2,其一侧的电压频率在(fS+fR)/2~fS的范围内周期性变化,另一侧的电压频率在fR~(fS+fR)/2的范围内周期性变化。
3 基于频率特征的失步解列判据
正常运行的电力系统中各发电机以同步转速运行,各发电机的电动势都以同样的工频角频率旋转,各电动势之间的相位差维持不变[9],此时电流频率和电压频率均为工频频率。当发电机输入或输出功率发生变化,其功角δ需要经过若干次在新的功角值附近振荡之后才能稳定,这一过程即同步振荡,此时包括频率在内的电气量出现摆动且以平均值为中心进行振荡。如果电力系统受到某种干扰,发电机功角δ在0°~360°之间周期性地变化,称作电力系统异步振荡[14]。通过上文的分析可知,此时电压频率具有如下特征:
a.振荡中心同一侧的电压频率同时增加或同时减小;
b.振荡中心两侧的电压频率没有交集;
c.对于振荡中心的两侧,若一侧电压频率增加,则另一侧电压频率减小;反之若一侧电压频率减小,则另一侧电压频率增加。
设 f1(k)和 f2(k)分别为某元件两端测得的电压频率,定义和,则有:
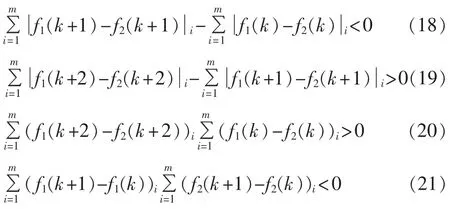
其中,m为求和的次数,对差值进行求和运算可以避免差值为零,同时起到抑制噪声、降低测量误差的作用。当同时满足式(18)和式(19)时可以判定系统内发电机功角出现振荡;同时满足式(18)—(21)时可以判定振荡中心在该元件上,因为振荡中心的两侧,若一侧电压频率增加,则另一侧电压频率减小,而振荡中心同一侧的各处电压频率同时增加或同时减小。
上述分析可以表示为图6所示的流程图。

图6 失步振荡识别流程图Fig.6 Flowchart of out-of-step oscillation identification
4 仿真与分析
仿真系统采用IEEE 3机9节点数据,如图7所示。线路参数考虑线路损耗和分布电容的影响,机组参数考虑励磁和调速器。利用BPA软件对该系统进行暂态仿真研究。设0周期时线路B-3上母线B近端发生三相短路事故,保护第一次动作失误,经过19个周期即0.38 s故障线路被切除,故障后系统发生失步振荡。

图7 IEEE 3机9节点测试系统Fig.7 IEEE 3-generator 9-bus test system

图8 G1与G3之间功角差Fig.8 Power angle difference between G1and G3
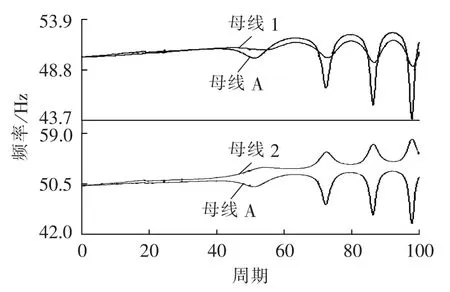
图9 线路两侧电压频率波形图Fig.9 Voltage frequency waveforms of both sides
图8为软件自动监控的仿真过程中最大发电机功角差,发生在G1与G3之间,可见在大约60个周期后发电机功角差δ在0°~360°之间周期性地变化,系统进入失步运行过程中。各条线路两侧母线电压值可以由BPA测得。图9分别为线路1-A和线路2-A两侧电压频率(基于50 Hz的相对值),可见振荡中心位于线路2-A上,线路1-A处于振荡中心的一侧。仿真过程中一周期采样10个点,即步长为0.002 s,根据式(18)—(21),取 m=3,将线路 1-A 两侧电压频率采样值代入图6所示的流程图,判据在1.104 s判断出系统失步振荡但振荡中心不在此线路上;对于线路2-A,判据在1.27 s判断出系统失步振荡且振荡中心在此线路上。
5 结语
通过理论分析及仿真验证表明,当系统发生失步振荡时,不论两侧电动势幅值是否相等,电压频率都具有以下特征:振荡中心同一侧的电压频率同时增加或同时减小;振荡中心两侧的电压频率没有交集;若振荡中心一侧电压频率增加,则另一侧电压频率减小,反之若一侧电压频率减小,则另一侧电压频率增加。从而提出一种新的基于频率特征的失步解列判据,该判据可以对同步振荡和失步振荡进行区分,识别振荡中心的位置,同时能够自适应于系统结构和运行方式的变化。

