交直流系统的静态电压稳定预防控制

户秀琼 ，颜 伟 ，余 娟 ，李文沅

（1.重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400044；2.BC Hydro公司，加拿大 温哥华 V7X 1V5）

0 引言

高压直流 HVDC（High Voltage Direct Current）输电由于其输送容量大、损耗小、功率调节迅速灵活、非同步联络能力强等优点，在大区电网互联、远距离大容量输电及跨海峡送电等方面得到了十分广泛的应用。但直流系统在为受端交流系统提供电力的同时，需消耗的无功功率约为直流传输功率的40%～60%，这使得与直流系统相连的交流系统的电压稳定问题变得十分重要［1-2］。特别是对于我国日趋复杂的交直流输电网络而言，由于电力市场的推进及负荷的增长，电力系统长线路、重负载及无功储备不足所带来的隐患逐渐显现，在某些运行方式下与直流系统相连的交流系统就呈现出弱交流系统特征，极易使交直流系统引发静态电压稳定问题，严重时会导致直流系统发生换相失败，进而恶化交直流系统的运行状态［3］。故为提高交直流系统的输送能力及输电的安全稳定极限，从而提高电网的可控性，需深入地研究预防控制措施，以加强安全控制中的第一道防线，防止交直流系统发生静态电压失稳事故［4-7］。

现有的针对静态电压稳定的预防控制主要集中在交流系统方面［8-13］，针对交直流系统静态电压稳定问题的预防控制却少有研究。文献［14］提出基于逐个严重故障的交直流系统静态电压稳定预防控制优化模型，并采用预测-校正原对偶内点法求解，但其未充分考虑直流控制方式对预防控制的影响，而且针对某一预想故障所得预防控制策略无法保证系统在其他预想故障状态下的静态电压稳定性，从而导致无法获得对所有预想故障均有效的预防控制策略。

本文在确定出所有不满足静态电压稳定裕度要求的关键预想故障的基础上，充分考虑直流控制方式对预防控制的影响，建立包含关键预想故障状态下交直流系统静态电压稳定裕度约束及正常运行状态下可行性约束的预防控制优化模型。该模型具有全二次特点，当采用预测-校正原对偶内点法求解该优化模型时，可在一定程度上降低模型的求解难度。

1 交直流系统的静态电压稳定预防控制模型

1.1 模型的数学描述

1.1.1 预防控制的目标函数

静态电压稳定预防控制的目标往往是以尽可能小的控制代价保证系统在正常运行方式及预想故障状态下均具有足够的静态电压稳定裕度。在交流系统的预防控制中，其控制措施包括调节发电机有功和无功出力、投切可调电容器和电抗器、调节有载调压变压器分接头以及切负荷［11］。而在交直流系统的预防控制中，还需考虑换流变压器分接头的调节。因此，本文所提预防控制优化模型的目标函数见式（1）。

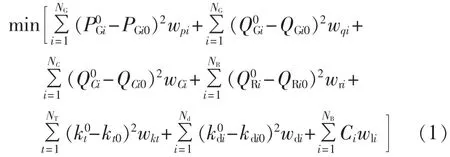
其中，PGi、QGi、QCi、QRi、kt、kdi分别为发电机有功出力、无功出力、可调电容器注入无功、可调电抗器注入无功、有载调压变压器变比、换流变压器变比。当前运行状态下（预防控制之前的正常运行状态）的运行变量以下标“0”表示，预防控制后正常运行状态下的变量以上标“0”表示；Ci为负荷节点切除的有功负荷量；NG、NB、NC、NR、NT、Nd分别为发电机节点数、系统节点数、可调电容器组数、可调电抗器组数、有载调压变压器台数以及直流节点数（换流站个数）；wpi、wqi、wri、wCi、wkt、wdi、wli分别为各个控制措施的权重，在实际工程中，发电机的有功和无功调节成本相对较低，因此其权重可取为0.1，而可调电容器、可调电抗器、有载调压变压器以及换流变压器的调节成本相对较高，其权重可取为1，切负荷的成本比其他控制措施的控制成本稍大一些，其权重可取为10［11］。

1.1.2 正常运行状态下的可行性约束

预防控制后的交直流系统，需要满足正常运行状态下的可行性约束。这些约束如式（2）—（27）所示。

其中，PDi、QDi分别为当前运行状态下系统各节点有功、无功负荷；Udi、Sdi、Pdi、Qdi、Idi、kdi、cos θdi、Umdi、Ui、ei、fi分别为直流电压、换流站的视在功率、直流系统传输的功率、换流站吸收的无功功率、直流电流、换流变压器变比、换流器控制角余弦、对换流变压器引入虚拟节点之后的虚拟交流节点电压幅值［15］、与换流站相连的交流节点电压幅值、系统节点电压的实部和虚部；kbi为直流系统每极中6脉波换流器的个数；kpi为直流系统的极数；xdi为换流变压器的换相电抗；gdij为直流网络节点电导矩阵的第i行第j列元素；xd1i、xd2i分别为直流控制变量 Udi、Idi、Pdi、cos θdi、kdi中的某一个，上标sp表示指定的常数；η=0.995为常数；SLi、STi分别为与节点i相连的线路支路集合以及有载调压变压器支路集合；PLij、QLij、PTij、QTij分别为线路支路传输的有功功率与无功功率、有载调压变压器支路传输的有功功率与无功功率，它们的具体表达式可参考文献［15］。

式（2）、（3）为交直流系统潮流方程，当与节点 i相连的换流器为整流器时，sPi=1；与节点i相连的换流器为逆变器时，sPi=-1；当节点i为纯交流节点时，sPi=0；当节点i直接与换流站相连时，sQi=1，否则，sQi=0。 式（4）、（5）为在有载调压变压器支路中引入虚拟节点之后的电压转换方程［15］。 式（6）—（10）为直流系统的换流器特性方程。式（11）为直流系统网络方程。式（12）为交直流系统的联合方程。式（13）、（14）为直流系统的换流器控制方程。式（15）—（27）为交直流系统中各个变量的上下限约束。

1.1.3 预想故障状态下的静态电压稳定裕度约束

对于交直流系统静态电压稳定预防控制而言，除了要求预防控制后的系统在正常运行状态下满足可行性约束之外，还要求系统在正常运行状态以及预想故障状态下均能满足静态电压稳定裕度约束。为方便说明，此处将有静态电压稳定裕度要求的正常运行状态作为预想故障状态的一个特例。

预想故障状态下的静态电压稳定裕度约束可用1.1.2节的交直流系统潮流方程、有载调压变压器支路中引入虚拟节点后的电压转换方程、直流系统换流器特性方程、直流系统网络方程、交直流系统的联合方程、直流系统的换流器控制方程及交直流系统中各变量的上下限约束描述。但有以下几点不同。

a.预想故障状态下的静态电压稳定裕度约束所包含的方程中，各个变量不再以上标“0”来表示，而是以上标“c”来表示，以此说明该变量属于预防控制之后预想故障状态下的变量。

b.可调电容器、可调电抗器、有载调压变压器及换流变压器在预想故障状态下可认为来不及动作，保持为预防控制后的正常运行状态值。因此，在预想故障状态下的静态电压稳定裕度约束所包含的方程中，这些变量的上标仍以“0”来表示。同时，在静态电压稳定裕度约束所包含的不等式约束中，不再有可调电容器注入无功、可调电抗器注入无功、有载调压变压器变比及换流变压器变比的上下限约束。

c.在预想故障状态下，交直流系统需要满足给定的静态电压稳定裕度。因此，预想故障状态下的交直流系统潮流方程表示形式不同于1.1.2节中的式（2）、（3），而应该用下面的式（28）、（29）来表示：

其中，λc为系统在第c个预想故障下需要满足的静态电压稳定裕度期望值，可由实际工程需要确定。

1.2 预防控制优化模型的特点

上述预防控制优化模型具有以下特点。

a.该模型中的直流控制方式可以指定1个、2个或不指定任何控制变量。当所有直流控制变量都参与调节以尽量保证交直流系统的静态电压稳定性时，则可将直流系统的换流器控制方程从模型中去掉，即不指定任何直流控制变量，所有直流变量在预防控制过程中不受限于某一给定值，而是可以在其上下限约束范围内变化。若每个换流站的直流控制变量只指定了1个，则每个换流站中的直流系统换流器控制方程仅需保存1个，同时在模型中去掉该控制变量对应的上下限约束。由此可见，该预防控制模型能灵活地考虑不同直流控制方式对预防控制的影响，从而为系统提供有利的预防控制方案。

b.模型中等式、不等式约束及目标函数是预防控制优化变量的一次或二次函数。故采用预测-校正原对偶内点法求解时，其海森矩阵为常数，不需在每次优化迭代过程中更新，从而可降低模型的求解难度。

2 交直流系统静态电压稳定预防控制的求解步骤

本文所提电压稳定预防控制的求解步骤如下。

a.获取交直流系统的初始运行状态。

b.采用文献［16］提出的交直流电压稳定临界点非线性规划算法，对每个预想故障状态下的系统静态电压稳定性进行分析。将不满足静态电压稳定裕度要求的预想故障作为关键预想故障。如果所有的预想故障都满足静态电压稳定裕度要求，则停止计算，并输出预防控制结果；否则，转入步骤c。

c.对关键预想故障，根据1.1节建立全二次预防控制优化模型，采用预测-校正原对偶内点法求解。

d.采用所得到的预防控制结果对初始运行状态下的交直流系统控制变量进行调整，并返回到步骤b。

3 仿真分析

3.1 测试系统简介

为了验证本文所提预防控制策略的正确性和有效性，现将IEEE 14节点交流系统改造成交直流系统。其结构图如图1所示，其中直流系统的具体信息如下：整流侧在节点5，逆变侧在节点4，直流系统极数为2，每极中6脉波换流器个数为1，直流线路电阻为10 Ω，换相电抗为26.75 Ω。

图1 改造后的IEEE 14节点交直流系统结构图Fig.1 Structure of modified IEEE 14-bus AC/DC system

3.2 仿真结果分析

为了使该交直流系统在故障或者重负荷情况下有可能出现静态电压稳定问题，将各个负荷节点的负荷增加为原来负荷的1.25倍。根据实际工程要求，正常运行状态下，静态电压稳定裕度期望值λ取为0.15；预想故障状态下，λ取为0.1。

采用交直流系统电压稳定临界点非线性规划算法对该系统的静态电压稳定进行分析。此处为了尽可能得到系统较大的静态电压稳定裕度，在利用该方法对系统的静态电压稳定性进行分析时，不指定直流系统控制方式，亦即所有的直流控制措施均参与控制。由此可以得到预防控制之前的关键预想故障，如表1所示。由表1可知，该系统在这2个关键预想故障状态下的静态电压稳定裕度都小于0.1，不满足静态电压稳定裕度要求。

在对以上不满足静态电压稳定裕度要求的关键预想故障实施预防控制时，为考察在预防控制过程中，不同直流控制方式对预防控制结果的影响，本文从以下几个方面进行了仿真分析。

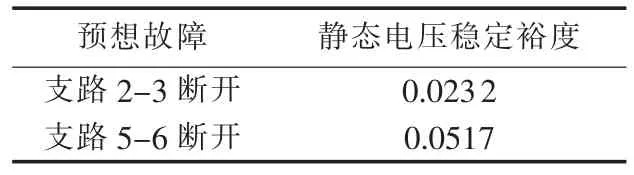
表1 预防控制前的关键预想故障Tab.1 Critical contingencies before preventive control

a.不指定直流控制方式。在预防控制过程中，所有的直流控制措施都参与调节。

b.整流侧定电流、逆变侧定电压。在预防控制过程中，整流侧电流和逆变侧电压保持其设定值不变。

c.整流侧定电流、逆变侧定控制角。预防控制过程中，整流侧电流和逆变侧控制角保持设定值不变。

d.整流侧定功率、逆变侧定电压。在预防控制过程中，整流侧功率和逆变侧电压保持其设定值不变。

e.整流侧定功率、逆变侧定控制角。在预防控制过程中，整流侧功率和逆变侧控制角保持其设定值不变。

针对这几个方面建立预防控制优化模型时，对于情况a而言，需要去掉所有直流系统换流器控制方程，同时在模型中去掉相应直流控制变量的上下限约束。对于后面4种情况而言，对每个换流站仅需要保留1个换流器控制方程，同时去掉指定直流控制变量所对应的上下限约束。

在指定直流控制方式时，所指定的直流控制变量的设定值取为系统在实施预防控制前的潮流状态值。其中，整流侧电流设定值逆变侧电压设定值，逆变侧关断角设定值整流侧功率设定值

对测试系统分别采用以上5种控制方式实施预防控制，其预防控制结果如表2所示。

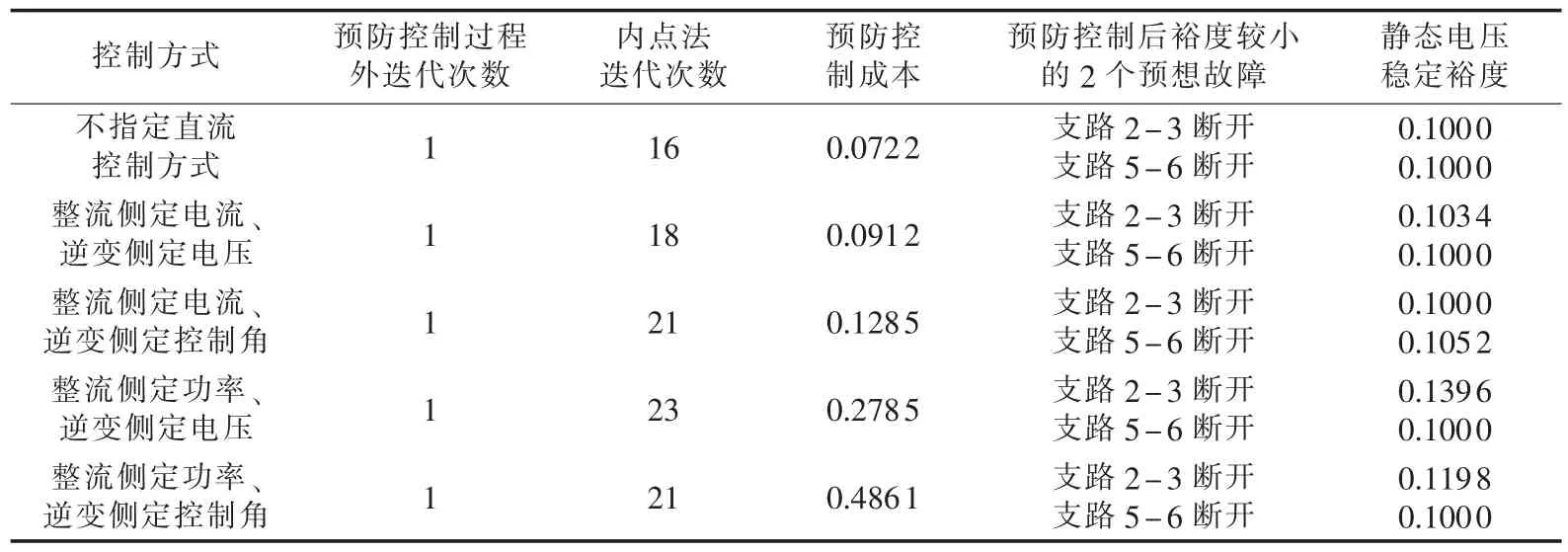
表2 各种控制方式下的预防控制结果Tab.2 Results of preventive control for different DC control modes

由表2的第2、5、6列可以看出，各种控制方式下，采用本文所提的预防控制策略经过1次预防控制，就能使系统在各种预想故障状态下均满足静态电压稳定裕度要求，从而说明了本文所提交直流预防控制策略的正确性和有效性。

由第3列可以看出本文采用预测-校正内点法求解预防控制优化模型是有效的。

从第4列的结果中可以看出，不指定直流控制方式（所有的直流控制措施都参与调节）时，系统的预防控制成本是最低的。而其他几种指定直流控制方式的情况中，整流侧定电流、逆变侧定电压控制方式下的预防控制成本较低，而整流侧定功率、逆变侧定控制角控制方式下的预防控制成本最高。由此可以说明，在对交直流系统实施静态电压稳定预防控制时，让所有的直流控制措施都参与调节，不但能保证系统在各种状态下均满足静态电压稳定裕度要求，而且能使控制成本达到最小。

对照表2的第4列与第6列的结果可知，不指定直流控制方式下的预防控制成本较低，但是预防控制后的系统在预想故障下的静态电压稳定裕度刚好满足运行要求；而指定直流控制方式下的预防控制成本较高，但预防控制后的系统在预想故障下的静态电压稳定裕度则较期望裕度稍大。因此，本文的仿真结果分析还可以提供给系统运行调度人员一个信息：如果想要预防控制之后系统的静态电压稳定裕度大一些，则可以采用控制成本较高的指定直流控制方式下的预防控制；如果想要预防控制之后的系统刚好满足静态电压稳定裕度要求，则可以采用控制成本较低的不指定直流控制方式下的预防控制。

4 结论

本文针对交直流系统提出一种防止其静态电压失稳的预防控制策略。该策略针对交直流系统中不满足静态电压稳定裕度要求的关键预想故障，建立了包含交直流系统正常运行状态下的可行性约束及关键预想故障状态下的静态电压稳定裕度约束的预防控制优化模型。该模型兼顾了直流系统的常规控制方式，具有全二次特点。对修正 IEEE 14节点交直流系统的仿真分析，证明了所提预防控制策略的正确性和有效性，并说明了交直流系统中各种常规直流控制方式对预防控制结果的影响，从而为交直流系统的静态电压稳定预防控制提供一定的理论支持。