基于稳定性分析的平衡闪蒸计算

李剑峰 贺 三 夏 丹 任建勋 梁 颖

西南石油大学石油工程学院，四川 成都 610500

0 前言

相平衡计算是石油化工工业的基础工作之一，在新技术理论研究中占有重要地位。例如模拟计算高含硫气田水闪蒸分离后闪蒸气中H2S的含量，以判断焚烧后SO2排放量是否满足污染物排放要求［1］；液化天然气低温脱除CO2时，须分析闪蒸分离的条件对分离效果的影响［2］；在 NGH（天然气水合物）储运中，研究如何改善NGH生成的相平衡条件［3］等，都需要进行大量的平衡闪蒸计算。

由于相平衡计算前混合物相数未知，因此计算的重要一步是核实闪蒸问题是否成立。当在给定条件下混合物会产生相分离时才进行平衡闪蒸计算。通常可采用的一种方法是求出给定温度下的饱和压力［4-6］，饱和压力以下混合物会形成两相。该法需要先确定饱和点的类型（泡点或露点），对于近临界区以外的烃类混合物，可通过相关经验法则实现［7］。但混合物在给定条件下可能不存在饱和点；对于某些混合物，在一定温度下可能存在两个露点，在较低的露点以下是单相的。另外，当计算出现问题时，也很难判断是不存在饱和点，还是迭代过程出现了数值问题［8］。

严格来说，确定给定条件下相分离与否，是从所有可能的相组合和组分分布中找到体系Gibbs自由能处于最低状态的条件［9］。当Gibbs自由能未达到最小时，混合物就会形成两相或多相。该法除判断相分离外，也可以为随后进行的闪蒸计算提供适当的初始值估计。

当稳定性分析显示混合物能形成两相或多相时，采用连续代入法进行指定相数的闪蒸计算。连续代入法形式简单，能满足大多数闪蒸计算的要求。

1 稳定性分析

混合物达到相平衡时应满足：各组分物料守恒；各相的温度和压力相同；各组分在各相中的化学势相等。除此之外，在平衡状态下，体系的能量应处于所有可能条件的最低值，可表达为：

式中：G为体系的Gibbs自由能量，J。

对于一个假想的单相流体，在某压力下用状态方程计算的二元体系的摩尔Gibbs自由能见图1。与Gibbs自由能曲线相切的线上两点代表有相同的化学势（如B和D），表示B和D为两个平衡相。F点的混合物可通过分为B和D两相达到更低的能级（F变为F′），那么作为单相它一定是不稳定的。而A点为一个稳定的相，它不能分为B和D两个相，因为如果降到A′处的能级则会出现一相的摩尔分数为负值，这在物理意义上是不可能的。

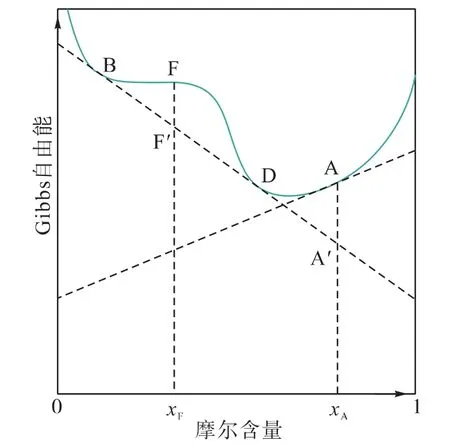
图1 某压力二元体系Gibbs自由能随组成的变化

对于多组分体系来说原理相同，只不过Gibbs自由能曲线变成了一个具有超切面的超曲面。可得到的结论是当Gibbs自由能面在所有浓度下都为上凹曲线时，混合物才保持一个稳定的单相，否则就会分成曲面和切面切点所指示的平衡相。判断混合物在给定条件下Gibbs自由能是否最小的过程称为稳定性分析，基于此原理得到的稳定方程为［10］：

式中：Yi为衡量新相中各组分物质的量的一个尺度；φi为各组分逸度系数，下标0和2分别代表原来的单相和可能形成的新相；zi为原有相中各组分的摩尔分数。

当混合物在给定条件下稳定时式（3）在所有解处恒大于等于0，因此需搜索其全局最小值。如果收敛时则混合物不稳定，需进行平衡闪蒸计算。

对于气-液两相分析，可用下式估算新相的组成，对于类液混合物：

对于类气混合物：

式中：Ki为相平衡常数。

通常情况下上述两组初值只需一组即可，对于烃类混合物，可选取仅由最轻组分或最重组分组成的单相。但对于不能清楚判断流体属性的临界区混合物来说都应作出估算。

Ki的初值用Wilson公式进行估算：

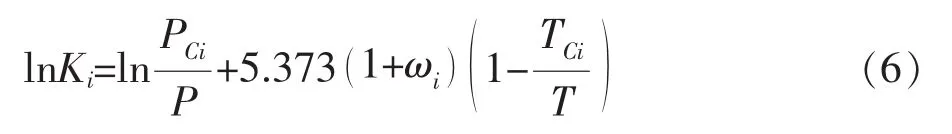
式中：PCi为各组分的临界压力，Pa；TCi为临界温度，K；ωi为偏心因子；P为体系压力，Pa；T为体系温度，K。

应用稳定性分析的好处是，当混合物不稳定时，收敛的Ki可为随后的闪蒸计算提供适当的初始值估计。这有助于临界区的计算，因为在临界区必须作严格的初始Ki的估算。

2 平衡闪蒸计算

为了方便用迭代法求解，一般选用Rachford-Rice方程，其值随β增加而单调递减，

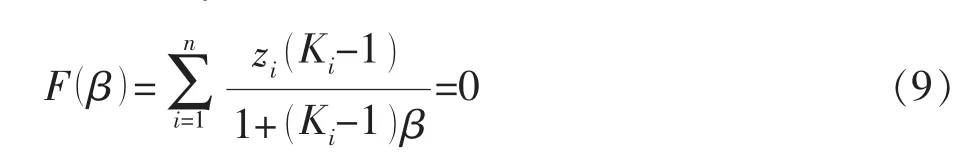
如果前面所述的稳定性分析显示混合物会发生相分离，则用收敛后得到的Ki作为初始值求解式（9）。用牛顿迭代法得到β的迭代公式为：

式中：k为迭代序号。

综上，闪蒸计算步骤可以描述为：a）由稳定性分析得到 Ki的初始值； 假设 β 初始值，0<β<1；b） 由式（10）迭代得到满足式（9）的 β解；c）根据式（7）、（8）计算得到xi和yi；d）根据状态方程计算气、液相的逸度系数和，得到 Ki的新值ε停止迭代，由式（9）得到正确的β解，进而得到汽、液相组成yi和xi，否则返回步骤b）继续迭代。

上述方法称为连续代入迭代法。为了在迭代循环中将β值控制在0～1内，可采用以下制约措施：当式（10）求出的 β（k+1）>1 时，则改取时，则改取

对于可能产生三相（LLV）的多相体系，也可利用连续代入法进行闪蒸计算。不同之处在于需对气-液两相闪蒸计算结果进行稳定性分析，即比较两相区和三相区Gibbs自由能大小。如果稳定性分析结果表明两相区的min（g）小于0，则进行多相闪蒸计算。

对于多相闪蒸，式（9）变为：

式中：Kim为各组分关于J相和m相的相平衡常数；βm为m相分率。βm仍可利用牛顿迭代法求解。

式（7）和式（8）变为：

式中：yiJ为J相中各组分的摩尔分数；yim为m相中各组分的摩尔分数。

3 计算举例

本文采用Peng-Robbison状态方程计算各组分的逸度系数。需要注意的是，当状态方程有三个实根（压缩因子根或摩尔体积根）时，应从最大和最小根中选出使体系Gibbs自由能较低的一个。状态方程所使用的各组分特性参数见表1。

石油与天然气混合物在发生汽化、冷凝或经过节流阀时，会因为温度和压力的改变而发生闪蒸分离的现象。考虑Mix1和Mix2两组典型的气体混合物，混合物摩尔组成见表2。

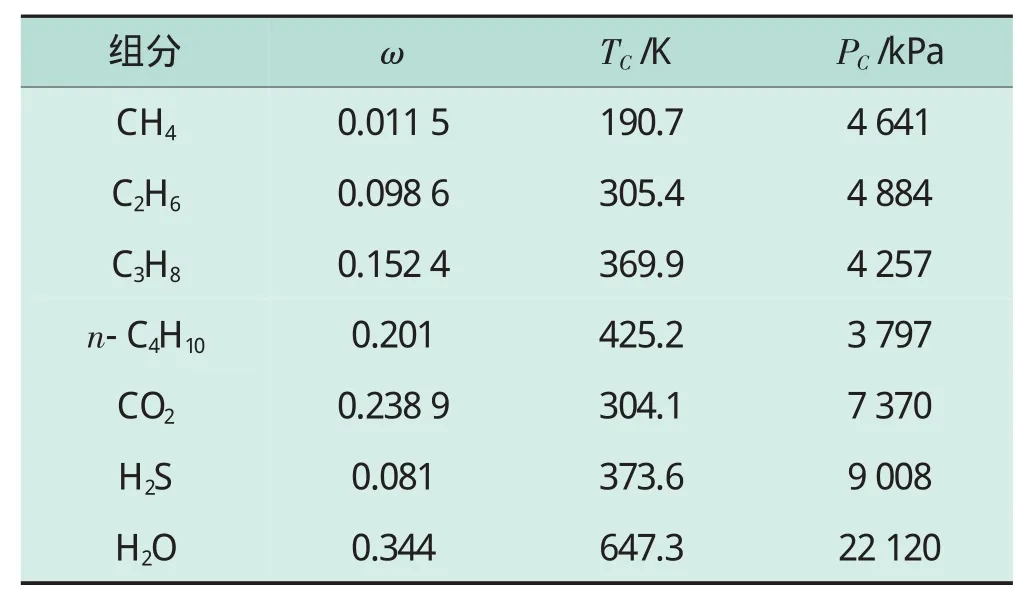
表1 各组分特性参数

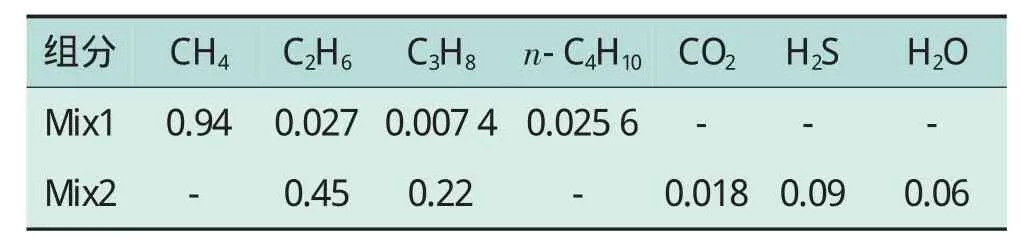
表2 混合物组成

进行稳定性分析时，本文采用适应性强的内点法搜索式 （3）的最小值，以避免传统的拟牛顿法 （如BFGS算法）可能出现求解失败的情况。对Mix1在不同条件下的稳定性分析的结果见表3。

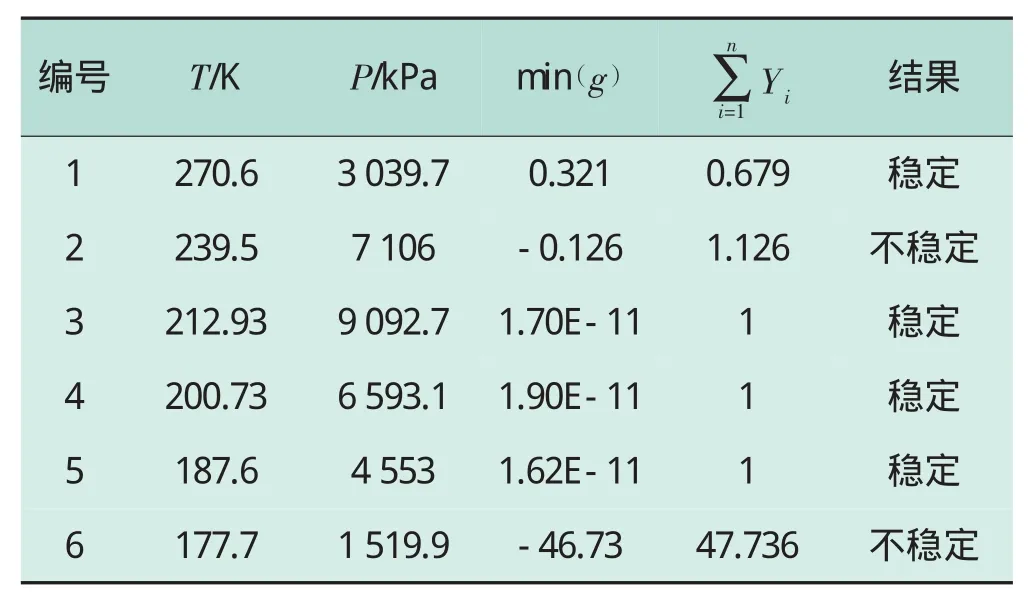
表3 Mix1稳定性分析结果

混合物在编号2和6的条件下是不稳定的，需进行平衡闪蒸计算。

由图2所示的混合物相包络线也可看出，点2和点6位于相包络曲线内的两相区。对于点1，混合物在该温度下不存在饱和压力，因此不能通过饱和压力来判断是否产生相分离。对于点2，在该温度下有两个露点，只有在较高的露点以下混合物才形成两相。然而利用稳定性分析可以快速有效地判断混合物的相数，减少不必要的麻烦。

对于Mix2，由于有烃和水的存在，在一定条件下液相会分成液烃相和水相。经稳定性分析计算得知，在温度为270 K、压力为1 500 kPa时混合物会产生相分离，用连续代入法进行闪蒸计算的结果见表4。

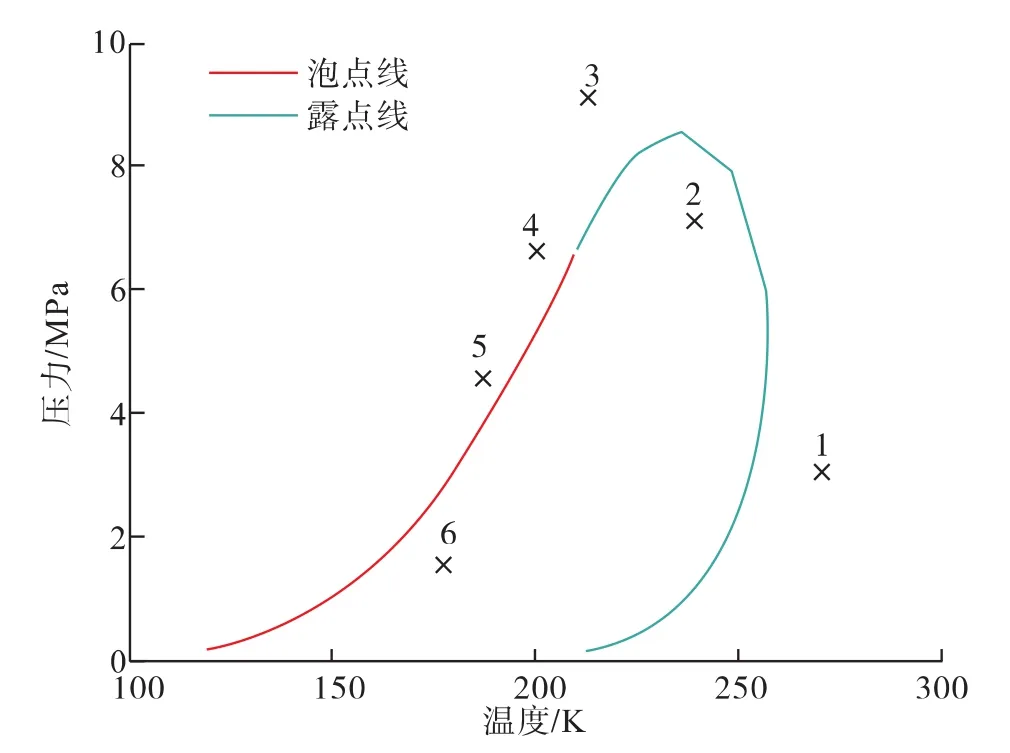
图2 Mix1相包络线

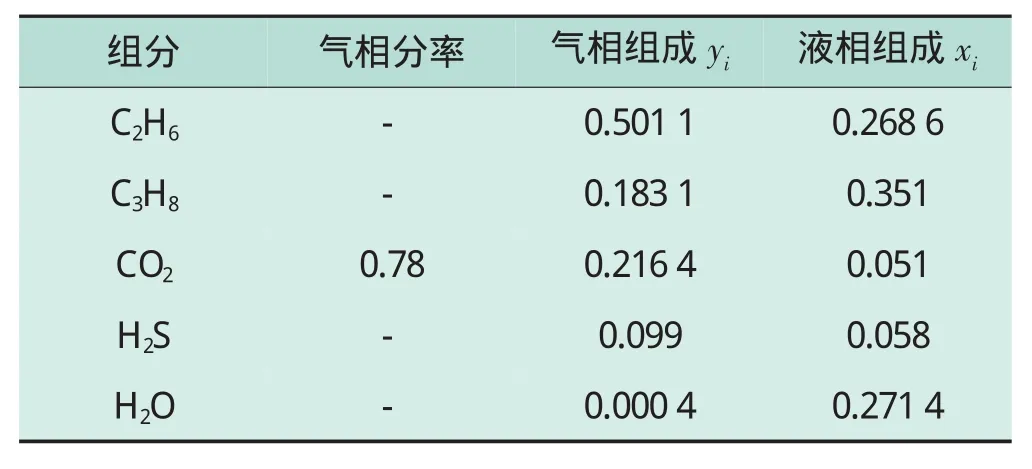
表4 Mix2闪蒸计算结果

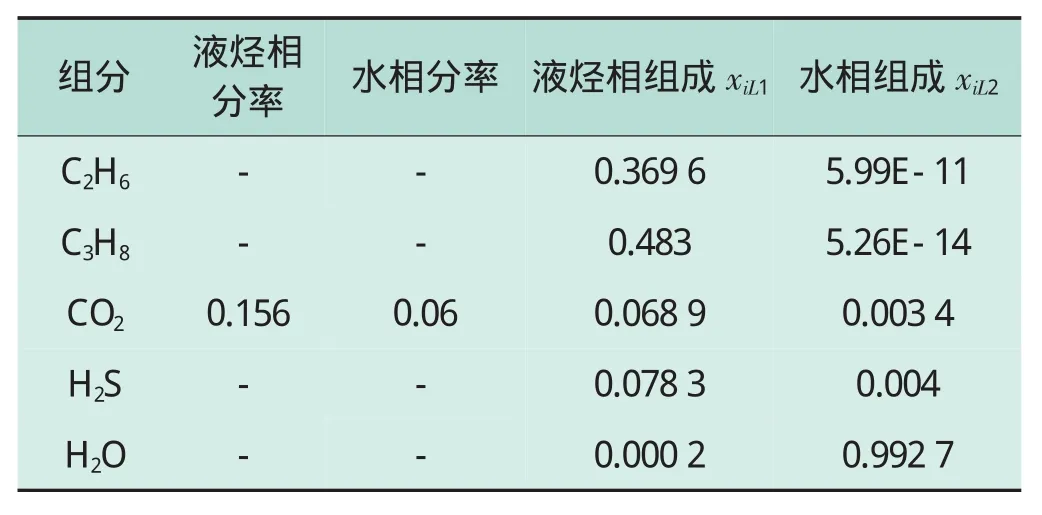
表5 Mix2液相闪蒸计算结果

对液烃相分析时发现，用式（4）和式（5）两组初值分别求解式（3）时，其中一组收敛于恒解xiL1，另一组收敛于汽相组成yi，而方程的值都为0。这证明了混合物处于Gibbs自由能最小的状态，并且达到了相平衡。

4 结论

本文将基于Gibbs自由能最小化原理的稳定性分析方法应用于平衡闪蒸计算，一方面可以很好地避免计算饱和点不能正确判断混合物相区的问题，一方面能得到闪蒸计算的严格解。稳定性分析判断混合物的相数，而连续代入法则计算对应于指定相数的各相组成。实例表明该方法是可靠的，计算结果也符合预期。

与采用单一状态方程计算各相逸度系数不同，也可通过活度系数模型表征液相行为。对于强极性体系，采用活度系数模型可以获得更高的精度。

［1］童富良，张永红.含硫气田水处置探讨［J］.天然气与石油，2008，26（1）：61-63.Tong Fuliang，Zhang Yonghong.Studies on Sour Produced W ater Treatment［J］.Natural Gas and Oil，2008，26（1）：61-63.

［2］熊晓俊，林文胜，顾安忠.CH4-CO2二元系低温分离方案的可行性探讨［J］.低温与超导，2012，40（1）：1-4.Xiong Xiaojun，Lin Wensheng，Gu Anzhong.Feasibility Study on Cryogenic Separation of CH4-CO2Binary System ［J］.Cryogenics and Superconductivity，2012，40（1）：1-4.

［3］巩 艳，林 宇，汝欣欣，等.天然气水合物储运天然气技术［J］.天然气与石油，2010，28（2）：4-7.Gong Yan，Lin Yu，Ru Xinxin，et al.Natural Gas Hydrate Storage and Transportation Technology ［J］.Natural Gas and Oil，2010，28（2）：4-7.

［4］陈洪钫，刘家祺.化工分离过程［M］.北京：化学工业出版社，2009.38-44.Chen Hongfang，Liu Jiaqi.Chem ical Seperation Process［M］.Beijing：Chem ical Industry Press，2009.38-44.

［5］白执松.石油及天然气物性预测［M］.北京：石油工业出版社，1995.139-147.Bai Zhisong.Oil and Gas Properties Prediction ［M］.Beijing：Petroleum Industry Press，1995.139-147.

［6］郭天民.多元气-液平衡和精馏［M］.北京：石油工业出版社，2002.161-170.Guo Tianm in.The Vapor-liquid Equilibrium and Distillation［M］.Beijing.Petroleum Industry Press，2002.161-170.

［7］Peng Dingyu.Accelerated Successive Substitution Schemes for Bubble-point and Dew-point Calculations［J］.The Canadian Journal of Chem ical Engineering，1991，69（4）：978-985.

［8］Karen SP，Peter L C.Phase Behavior of Petorleum Reservoir Fluids［M］.Boca Raton：CRC Press，2007.115-139.

［9］Baker L E，Pierce A C，Luks K D.Gibbs Energy Analysis of Phase Equilibria［J］.SPE Journal，1981，22（5）：731-742.

［10］Michelsen M L.The Isothermal Flash Problem，partⅠ：Stability Analysis［J］.Fluid Phase Equilibria，1982，9（1）：1-19.