基于响应面法某轿车后纵梁支架结构优化

魏 然，王显会，路先锋，吴 旭

（南京理工大学 机械工程学院，江苏 南京 210094）

0 引言

我国在2006年7月1日颁布实施了《乘用车后碰撞燃油系统安全要求》（GB20072-2006），这一强制性法规对车辆结构的耐撞性及燃油系统安全提出了更高的要求［1］。汽车追尾碰撞仿真中，通常以油箱周围结构的变形来考核燃油系统的完整性。后纵梁支架位于后纵梁尾端、油箱周围，如其耐撞性好，能够缩小汽车追尾碰撞中后纵梁及其他零件对油箱的挤压和破坏。为了使后纵梁支架具有合理的轴向压溃性并吸收更多的碰撞能量，有必要对后纵梁支架这一薄壁钣金件的结构进行耐撞性研究。

为了解决这一问题，在保证模型精度的前提下，可以采用试验设计对指定的设计点集合进行较少的试验，得到目标函数和约束函数的响应面模型来预测非试验点的响应值［2］。

1 研究方法及理论背景

1.1 试验设计（DOE）

为了减少有限元仿真的试验次数，同时获得精度较高的近似模型，需要事先制定好的试验策略和好的试验方法。常见的试验设计方法有全析因试验设计、正交试验设计、均匀试验设计、随机投点试验设计、拉丁方方法等［3］。

1.2 响应面法（RSM）

为了过滤后纵梁支架结构优化过程中可能产生的数值计算噪声，缩短计算时间，需要利用近似方法（Approxi mation approaches）对离散数据进行拟合的数学模型。常用的近似模型建模方法有人工神经网络法、Kriging函数法及径向基函数法等［4］。多项式响应

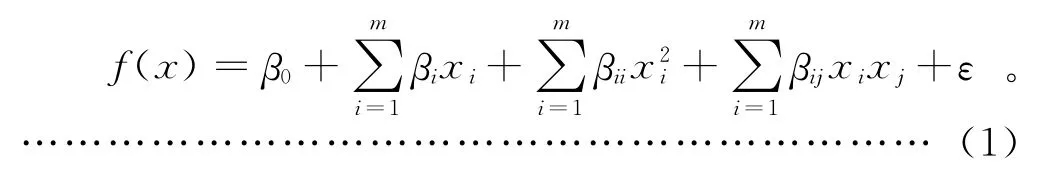
其中：β0、βi、βii、βij为待定系数；ε为拟合误差；i，j为1～m的整数，且j≥i。在得到响应表面后，可以通过方差分析中的两个参数决定系数R2和调整决定系数对响应表面模型的拟合程度进行验证。R2和Ra2dj是在［0，1］变化的数，其值越接近1，说明模型的拟合精度越高。这两个参数定义为：面是优化设计中最为常用的一种近似模型，响应面函数f（x）与试验点集合（x1，x2，…，x i，…，x m）之间的函数关系可以表示为：

其中：n为试验点的个数；l为自由度；y k、、分别为响应面函数f（x）的实测值、预测值和实测值的平均值。

1.3 优化方法

所有的优化问题都包括目标函数min（或max）f（x）、约束条件s.t.g（x）≥0、可行域x∈D，在构建了近似模型响应面之后，就得到了优化问题的目标函数。现代优化算法有模拟退火、遗传算法、神经网络等［5］。针对后纵梁支架追尾碰撞结构优化的非线性规划问题，适合使用的方法是遗传算法（Genetic Algorith m）。

2 优化问题描述

在某轿车的追尾碰撞试验和有限元仿真试验中均出现后纵梁支架明显压溃不足，如图1所示。这一现象直接导致后纵梁承受了较大的碰撞冲击载荷，产生大塑性变形，从而挤压油箱，造成油箱泄漏。为了减小后纵梁所受的碰撞冲击载荷，故需对后纵梁支架进行结构优化。

图1 某轿车油箱及后纵梁追尾碰撞有限元仿真

在对后纵梁支架进行一定的简化之后，建立后纵梁支架的限元模型，如图2所示。后纵梁支架末端固定，前方是一个重0.5 t并以4 m／s初速度撞击后纵梁支架的刚性墙。考虑到在对后纵梁支架结构优化中应避免大的改动从而不影响整车中其他零件，故设置后纵梁支架上三对弱化槽的位置L为优化变量，如图3所示。L1、L2、L3分别是三对弱化槽顶部相对于后纵梁支架尾部平面的距离，L1、L2、L3初始值分别为90 mm、140 mm、180 mm。

图2 后纵梁支架的有限元模型

图3 后纵梁支架侧视图

为了评价后纵梁支架的耐撞性，使刚性墙的动能全部被后纵梁支架吸收（即刚性墙碰撞后速度为0），后纵梁支架纵向变形量即刚性墙的位移越小，对后纵梁的保护效果越好，表明后纵梁支架吸能能力越高、耐撞性更好。故设置刚性墙的位移D（L1，L2，L3）最大（考虑到刚性墙运动方向为负，函数D越大，刚性墙位移越小）为目标函数。同时考虑碰撞的安全性要求，将撞击力峰值F（L1，L2，L3）限制在90 k N以内。由于薄壁结构的耐撞性与其材料、形状及厚度等参数有关，经过变量分析及实际设计中对结构改进工作时间、成本等因素的要求，从而选取形状变量为本优化问题的设计变量。利用Hyper morph网格变形定义L1、L2、L3形状变量。综上分析，本优化问题的数学模型为：

3 优化过程

后纵梁支架耐撞性结构优化过程可分为试验设计、响应面近似模型建立、通过遗传算法对数学模型优化、优化结果检验4个阶段。

试验设计选择正交复合试验设计方法［6］，利用显式有限元仿真技术代替传统试验来获取共17组试验设计点的响应数据，见表1。

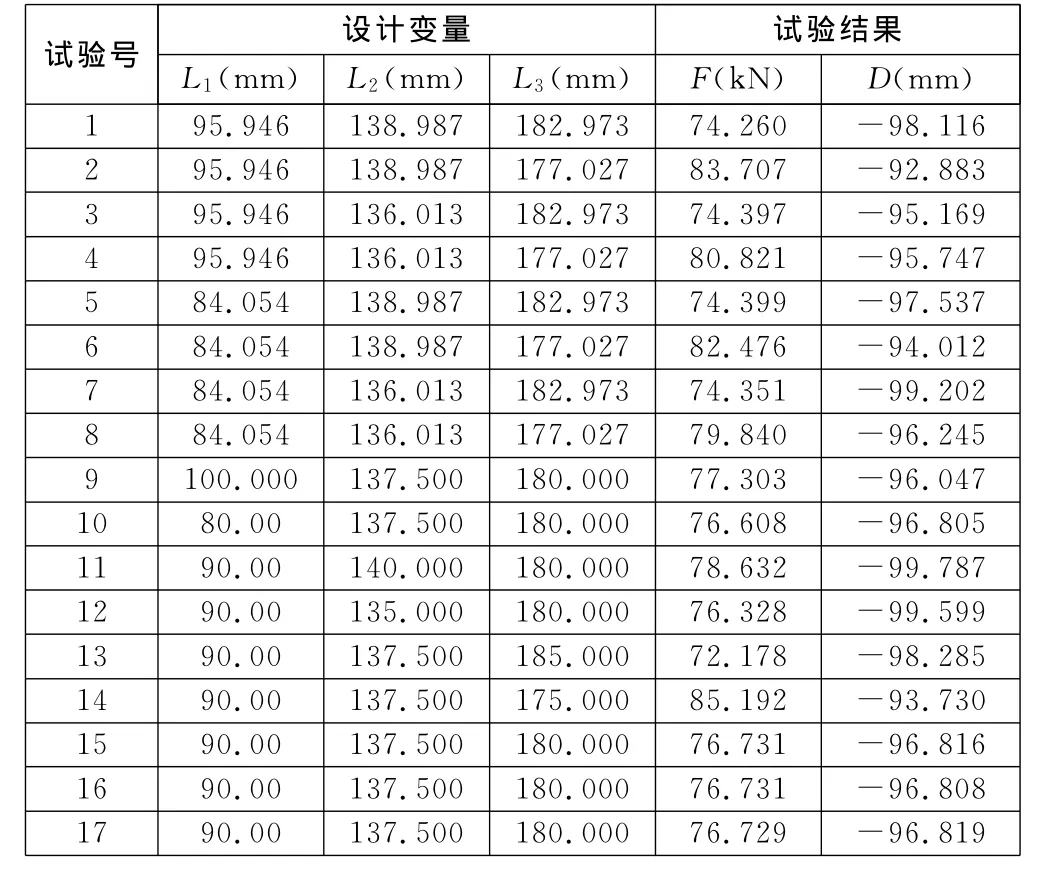
表1 本次结构优化正交复合试验方案及结果

完成17次试验并得到响应结果之后，使用最小二乘法来构建目标函数和约束函数的响应面近似模型［7］。为了保证近似模型的准确性，降低拟合误差，使得决定系数R2和调整决定系数R2adj的值尽量接近1，建立二阶响应面近似模型，其目标函数和约束函数的数学模型表达式如下：

式（5）为目标函数近似表达式，R2＝99.6%、＝99.2%；式（6）为约束函数近似表达式，R2＝99.8%、＝99.6%，两个方程拟合精度均达到工程要求。

将得到的拟合方程近似模型式（5）、式（6）分别代入数学模型式（4），再通过遗传算法（GA）对该优化问题的数学模型以L1、L2、L3初始值分别为90 mm、140 mm、180 mm进行优化求解，经过8次迭代后得到的L1、L2、L3的最优值分别为98.2 mm、139.61 mm、175.06 mm。在满足约束条件的情况下，刚性墙的纵向位移最小为89.632 mm。图4为优化前、后目标函数D（L1，L2，L3）随时间变化曲线的比较，由图4可知经过对后纵梁支架结构优化之后，经刚性墙碰撞后的纵向位移有明显减弱的趋势，其纵向位移的峰值的绝对值由优化前的99.599 mm缩小到优化后的89.632 mm，从而证明后纵梁耐撞性、吸能性得到提高。

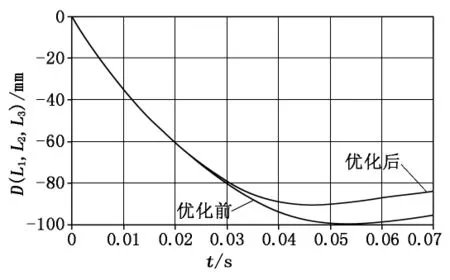
图4 目标函数优化前、后随时间变化曲线比较

为了检验后纵梁支架结构优化后对整个后纵梁总成耐撞性改善结果，将优化后的后纵梁支架与优化前的零件替换，再通过有限元仿真追尾碰撞试验，仿真结果如图5所示。由图5可知：在优化后由于后纵梁支架碰撞吸能效果不佳导致后纵梁大塑性变形的现象已经得到改善；且后纵梁支架由于采用了合理的吸能槽排布方式，有良好的逐步压溃的效果，将经受碰撞冲击波载荷后的变形模式限制在后纵梁支架附近，有效地防止了油箱周围其他零部件对油箱的挤压。

4 结论

优化后后纵梁支架的耐撞性得到显著提高，并且与整个后纵梁总成之间有良好的匹配，有利于改善整车追尾碰撞的耐撞性。该结构优化方法能用较小的计算成本来有效预测和指导提高工程实践中产品设计的吸能性和耐撞性，具有一定的实用与推广价值。

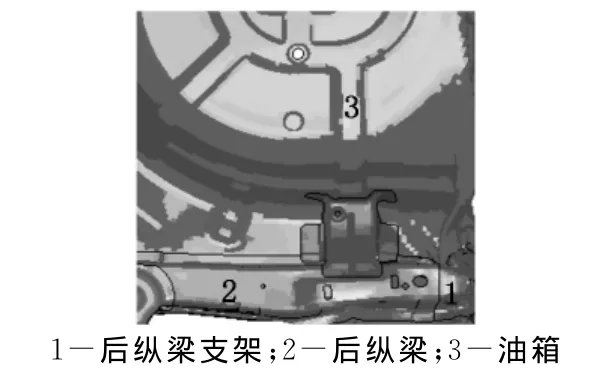
图5 优化后的油箱及后纵梁追尾碰撞仿真

［1］吴卫，汽车交通事故分析［J］.世界汽车，1996（3）：12-14.

［2］Redhe M，Forsberge J，Janssone T，et al.Using the response surface methodology and the dopti mality criterion in crashwort hiness related problems ［J］.Str uctural and Multidisciplinary Opti mization，2002，24（3）：185-194.

［3］Don V L.Analysis of the factors influencing side impact occupant injury［J］.SAE Paper 1999-01-0067.

［4］Bucher C G，Bourgund U.A fast and efficient response surface approach for structural reliability problems［J］.Structural Safety，1990，7（1）：57-66.

［5］Ghasemnejad H，Hadavinia H，Simpson G.Crashworthiness optimization of crash box in automotive structure［J］.Key Engineering Materials，2007，348：661-664.

［6］姚伟，汽车正面碰撞吸能元件耐撞性研究与结构优化［D］.上海：同济大学，2006：43-52.

［7］Wang H，Mullerschon H，Mehrens T.Shape optimization of a crash-box using Hyper morph and LS-OPT［C］／／Proc 4th Ger man LS-DYNA Forum.Bamberg：［s.n.］，2005：13-15.