《市场调查和预测》中直线方程的系数求解方法探讨

程定平

(湖南涉外经济学院, 湖南长沙 410205)

《市场调查和预测》是市场营销专业和工商管理专业的一门必修课程.该课程中市场预测的方法涉及不少的数学公式和数理统计知识,对于以学文科为主的市场营销专业和工商管理专业的学生而言,无疑具有一定的难度和挑战性.任课教师为了帮助学生理解各种预测方法,提高教学效果,需要对各种预测方法进行详细讲解,并辅以例题、案例教学,来达到帮助学生理解记忆的目的[1-3].笔者认为,除此之外,对前后知识点进行归纳总结,不仅可以复习巩固原有知识点的学习,还可以更好的理解学习新的知识点,同时,也有利于知识点的融会贯通.在各种市场调查和预测的教材中,均会介绍市场预测的方法.市场预测的方法可以分为定性和定量两种,定量的分析方法主要有时间序列分析法和因果分析法.时间序列分析法中的直线趋势延伸法和因果分析法中的一元线性回归,均会涉及到线性方程参数a、b的求解.本文专门针对线性方程参数a、b的求解列出几种不同方法,并配以例题讲解.

1 标准公式:利用最小二乘法和极值定理求解

直线方程系数的标准求解方法,就是根据最小二乘法的基本原理,即实际值与观察值 (预测值)的离差平方和最小,结合极值定理设立联立方程求解.

∑(Yt- Yt)2=最小,即∑(Yt-a-bt)2=最小

利用极值定理可以转化为联立方程:

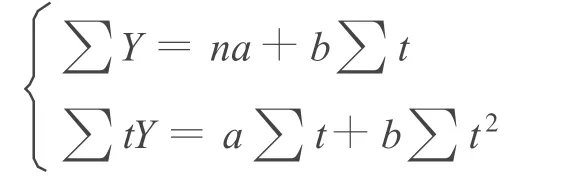
联立解方程得到参数a、b:

例题1 某市场的一种商品前9个月的销售量数据如下表1,根据销售量数据变化趋势试预测第10个月的销售量.

表1 某市场的一种商品的销售额

分析过程:通过做增量分析,得到增量范围为3～5,近似相等,因此可以拟合为线性趋势,建立数学模型:Y=a+bt,只要求解出参数a、b,即可进行预测.

计算过程:

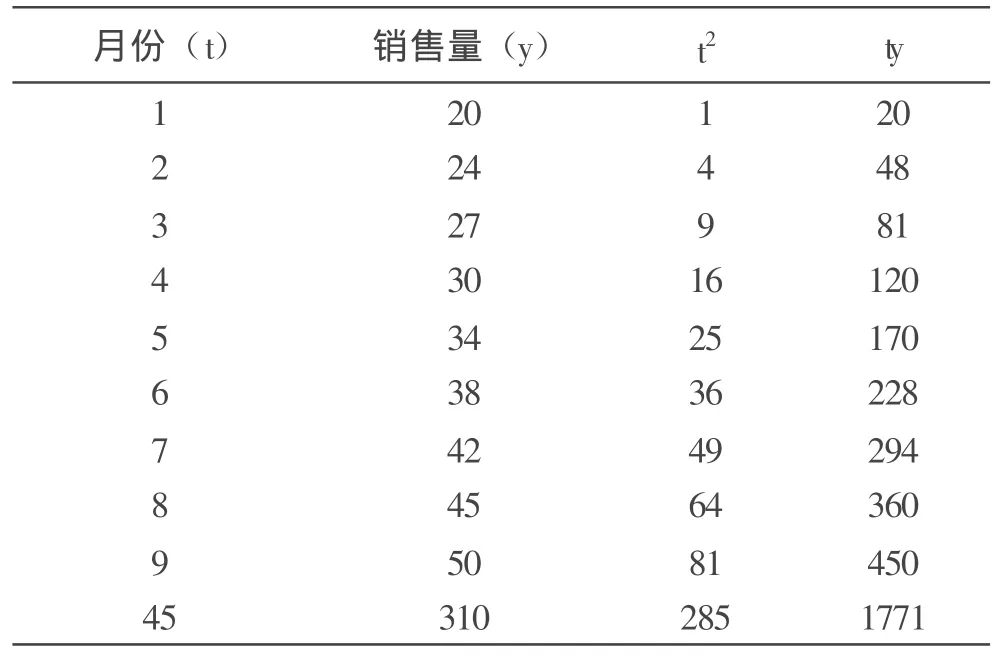
表2 标准公式中需要的数据计算

根据表2,将数据代入公式

代入参数a、b,即可得线性方程Y=16.04+3.68t所以,第10月的销售量的预测值就是t=10时的Y值,即

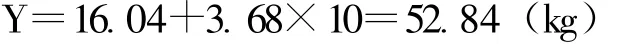
2 特殊公式:当∑t=0时可采用简易方法求解

对于时间序列,时间作为横坐标,仅标示位置,水平位置左右平移并不会影响纵坐标的预测值.因此若令 ∑t=0,参数a、b的计算公式就变得简单许多,将∑t=0代入标准公式:

可以得到简易公式:

仍以例题1为例,题目略.

计算过程:

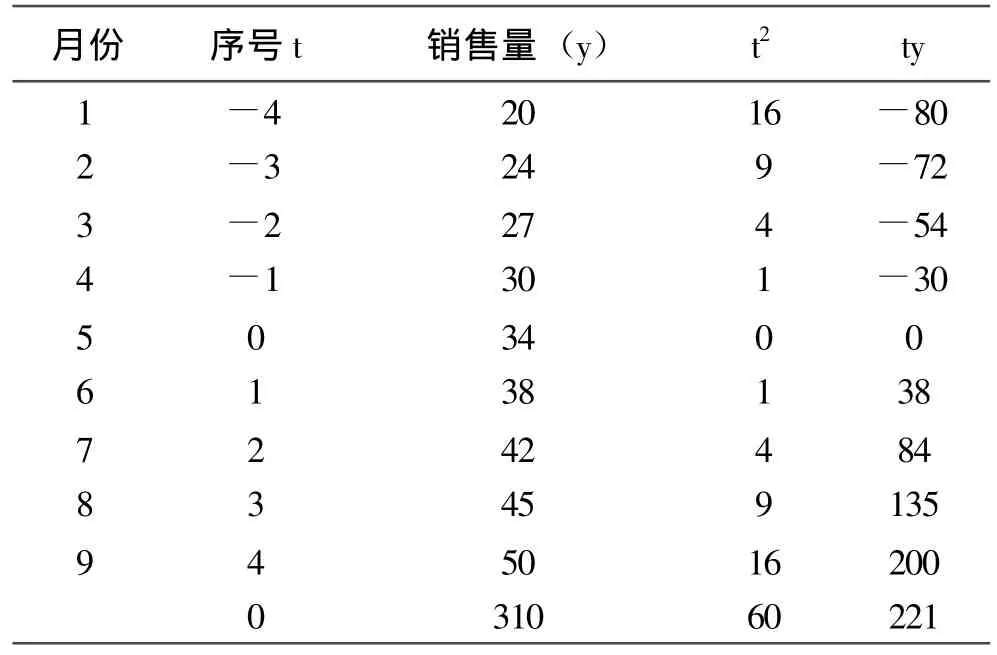
表3 特殊公式中需要的数据计算

将表3中的数据代入公式:

根据t的编数规律,第10月的t为5,将t=5代入公式:

用特殊公式计算的结果与标准公式计算出的结果是一致的.

3 变形公式:为方便计算机编程而引入新参数

为了方便计算机编程,通常先进行定义

这样,参数a、b的公式变为:

还以例题1为例,题目略.

分析过程:将公式中的X看成t,则Xi2=t2,Xi×Yi=t×y,将表2数据直接代入即可.

计算过程:

将参数 a、b代入,则Y=16.04+3.68X

若X=10,则Y=52.84,与前面的公式计算的结果完全吻合.

4 经验公式:斜率 b近似等于纵坐标差与横坐标间距的比值

在季节变动预测法中,可以用经验法计算线性方程的参数a、b.经验法是将收集的时间序列根据时间周期 (通常为一年)分成几段,分别计算第一段和最后一段的平均值,再与时间间隔期数相比得到斜率b,a则根据第一段的平均值和期数的均值得出,具体公式为:

由于本题中涉及季节变动,因此需要有季节变动的数据,故不再用例题1.本文将用一个具体的例题来介绍经验法如何计算线性参数a、b.

例题2 以某超市某种商品近三年每个季度的销量为例,具体数据如下表.

表4 某超市某商品三年的季度销售量 (单位:10 kg)

从数据看,具有明显的季节性,第三季度较其它三个季度明显要多出很多;从不同年份的相同时期可以看出,存在一定的线性趋势,因此,该商品的销售量存在线性趋势的季节变动.因此可以建立加法模型:Yt=a+bt+di或者是乘法模型:Yt=(a+bt)×fi.本文在这仅仅只介绍线性参数a、b的计算,不涉及季节指数的计算.

计算过程:

表5 某超市某商品的季节变动线性参数所需数据

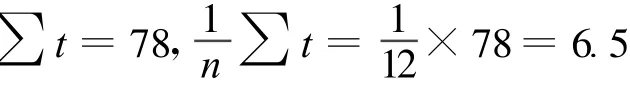
将数据代入公式:

则Yt=29.92+0.59t+di或者Yt=(29.92+0.59t)×fi.

此题如果简单地套用标准公式计算参数,则计算出来的参数为:

用标准方式计算出来的参数a、b与经验法计算出来的参数a、b相距甚远,原因有二:

(1)经验法只是估计值,误差较大;(2)本序列除了具有线性趋势外,还存在季节变动,必须剔除季节变动因素带来的影响才可以,此处不作讲解.

综合上述,公式罗列和例题示范,笔者对线性方程系数的各种计算方法的应用范围等以表格的方式进行简单归纳总结,以方便学生的对比理解记忆,具体内容见表6.

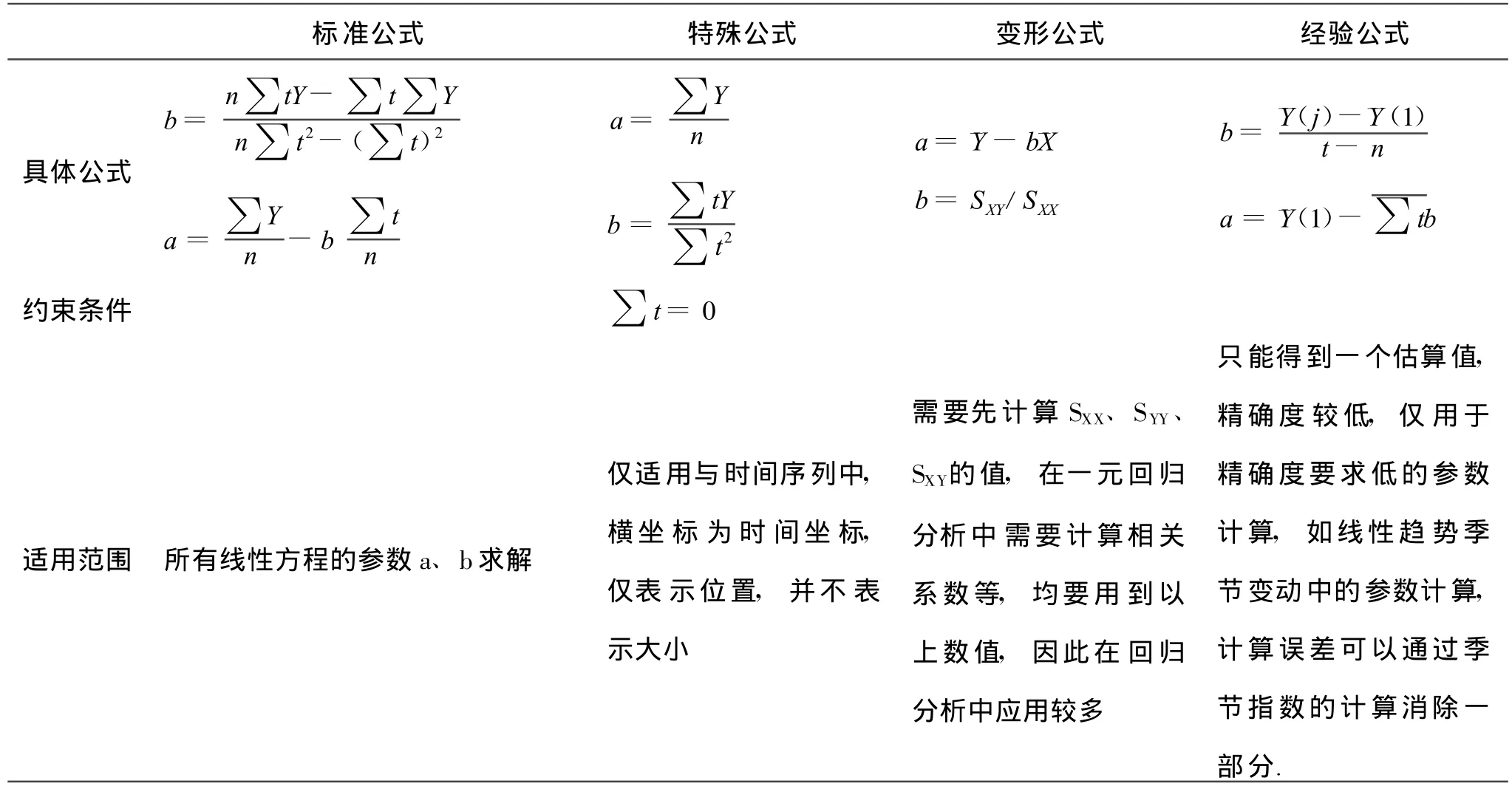
表6 四种公式的归纳总结

[1]简明,胡玉立.市场栅测与管理决策 [M].人民出版社,2010.

[2]范薇薇.“市场调查与预测”教学模式初探[J].江苏经贸职业技术学院学报,2009,(4):87-89.

[3]卢珊.案例教学在数据分析技术课程中的应用探讨[J].首都师范大学学报(社会科学版),2009,(12):18-21.