基于超声波气体传感器的飞行时间测量系统*

崔园园，王伯雄，柳建楠，李 伟

（清华大学精密仪器与机械学系精密测试技术及仪器国家重点实验室，北京 100084）

0 引言

进行超声波飞行时间测量需要保证其在环境噪声干扰下的测量精度，传统方法从发射脉冲和接收波形上选取起始和终止时刻，然后进行时间间隔测量［1～4］。在这种方法下，时间间隔测量精度虽然可以达到ps级，但受噪声因素影响，起止时刻的定位精度是值得商榷的［5］。数字相关方法可以将确定测量的起止位置与时间间隔测量2个步骤合为一体，从而减少不可信赖性，特别适用于气体环境或复杂噪声环境下进行飞行时间测量［6～9］。本文基于“双向回波法”的标定方法和数字相关法的飞行时间测量方法搭建了飞行时间测量系统，该系统能够满足超声波飞行时间测量的可信赖性和准确性，可以应用于距离、流量和风速测量等领域。

1 飞行时间测量方法

假定d1（n）和d2（n）分别为参考超声波信号和接收到的超声波信号，则d1（n）由无噪超声波信号s1（n）和噪声nd1（n）组成，d2（n）由s1（n）的衰减延迟形式As1（n－τ）和噪声nd2（n）组成。从数学上，它们可以表述为

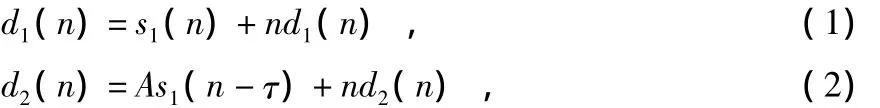
式中A是衰减系数，τ是两超声波信号之间的时间间隔。进行时间测量的目的就是获得对τ的准确估计。一般情况下，在式（1）与式（2）中，nd1（n），nd2（n）为白噪声，它们与超声波信号s1（n）互不相关。

d1（n）的自相关函数为

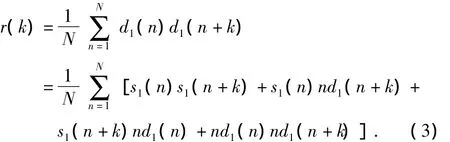
式中N为信号长度。式（3）中的第一项是无噪超声波信号s1（n）的自相关函数，第二项和第三项均为无噪超声波信号s1（n）和噪声nd1（n）的互相关函数，最后一项为噪声nd1（n）的自相关函数。基于前述关于信号和噪声相关性的描述，可知当N趋向于无穷时，后三项（除k=0点外）均趋于0。然而，因为N为有限的数值，噪声白化不充分，r（k）中仍含有噪声成分。r（k）可以表述为

式中Css（k）为无噪超声波信号s1（n）的自相关函数，n'1（k）为噪声。此时的噪声成分n'1（k）要远小于nd1（n）。与原始信号d1（n）相比，r（k）的信噪比得到提高。

d1（n）和d2（n）的互相关函数为

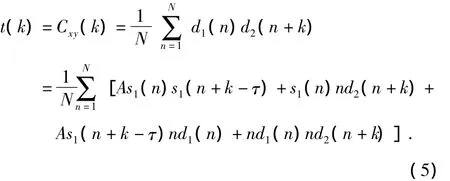
同样，由于无噪超声波信号和噪声之间不存在相关性以及噪声白化不充分，t（k）可以表述为

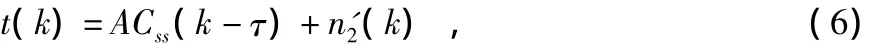
式中n'2（k）为噪声。同样地，n'2（k）比原始信号中的噪声成分nd1（n）和nd2（n）都小，t（k）的信噪比得到提高。由于Css（k）为无噪超声波信号s1（n）的自相关函数，理论上，Css（k－τ）在点k=τ取得最大值。然而，由于噪声n'2（k）的存在，t（k）的最大值点位于k=τ点附近。

将r（k）和t（k）做互相关运算可以进一步提高信噪比，两者的互相关函数g（l）为

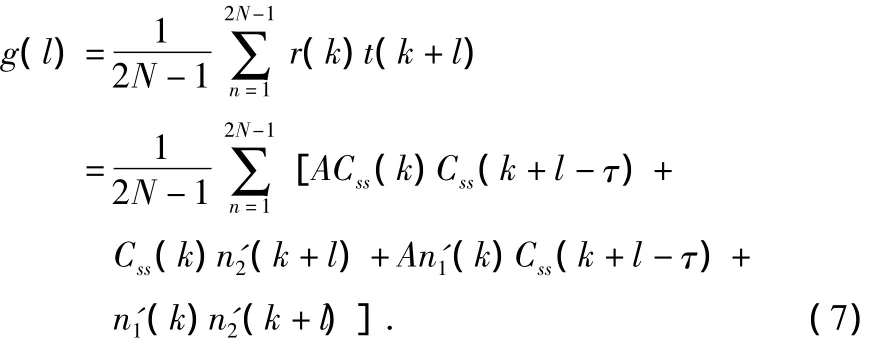
同样，由于信号和噪声之间不存在相关性以及噪声白化不充分，g（l）可以表述为

式中C2（k－τ）为Css（k）和Css（k－τ）的互相关函数，n″2（k）为噪声。同样地，n″2（k）比r（k）和t（k）中的噪声成分n'1（k）和n'2（k）都小，g（l）的信噪比进一步提高。由于C2（k－τ）在点k=τ取得最大值，故g（l）的最大值也位于该点附近。

由于利用快速傅里叶变换（fast Fourier transform，FFT）将信号变换到频域中进行频域相关运算更节省计算量，则式（3）可重新表述为

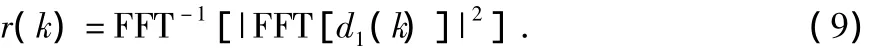
式中 ||代表取模运算。

同样，式（5）和式（7）可分别通过下式实现

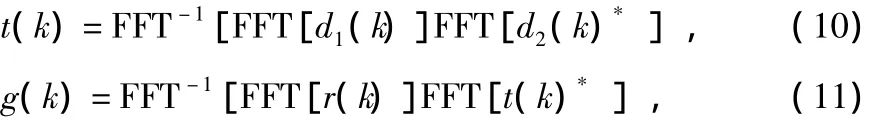
式中 *代表取共轭运算。

二重相关运算将超声波飞行时间测量的问题转化为搜索确定峰值点位置的问题。本文中的搜索定位方法基于Hilbert变换函数。首先，对式（11）进行Hilbert变换

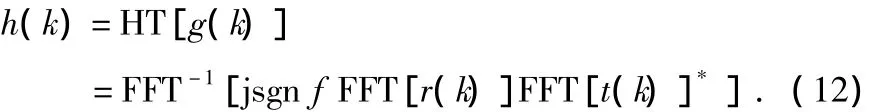
由图1可以看出:g（k）和h（k）具有相同的包络，g（k）的极大值、极小值对应h（k）的过零点，故h（k）具有很多过零点。

将二重相关函数中具有最大值的采样点位置作为粗略定位点，在该点附近向左右两方向进行搜索，寻找数值的符号发生变化的两相邻采样点，过零点即位于这两点之间。寻找到的两相邻采样点分别为过零点附近的最小正值点和最大负值点。在此处做线性插值即可获得对过零点的估计，如图1的放大框中所示。

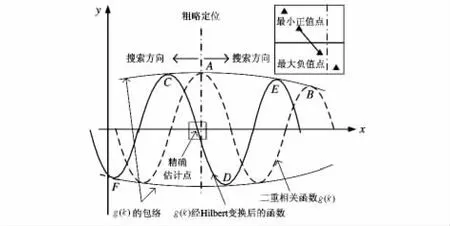
图1 Hilbert粗略定位点搜索法示意图Fig 1 Diagram of coarse location point searching method based on Hilbert transform

2 双向回波法

“双向回波法”是一种对测量系统的电路延迟进行标定的方法，它可以获取待测时间间隔的起点。气体超声波传感器A与B面对面放置。假定将A作为发射探头，其发射的信号传播到探头B被接收。与此同时，B将超声波反射后传播至探头A处被接收。图2中，以横轴为时间轴，上面的波形为外部介质中传播的真实超声波信号，分别为A刚发射出的波形、传播到B处的波形和返回至A处的波形。为方便起见，将波形的峰值点标示为发射和到达时刻，则3个波形之间的2个时间段长度均为超声波真实的传播时间t0。由于电路延迟的影响，如图2所示，发出激励脉冲的起始时刻与发射时刻之间存在固定发射延迟δ1，计算机接收到波形的时刻与到达时刻之间存在固定接收延迟σ2，计算机接收到回波信号的时刻与回波到达时刻存在固定接收延迟σ1。以发出激励脉冲的起始时刻为时间零点，则计算机记录的B接收到波形的时刻为δ1+t0+σ2，计算机记录的A接收到回波波形的时刻为δ1+2t0+σ1。两者之间差值为 Δt1=t0+σ1－σ2。

由于不同的接收板延迟存在差异，σ1与σ2不能完全抵消。此时，选择B为发射探头，利用上面的方法进行二次测量。此时，计算机记录的A接收到波形的时刻为δ2+t0+σ1，其中，δ2为B的发射延迟。计算机记录的B接收到回波波形的时刻为δ2+2t0+σ2。两者之间的时间差为Δt2=t0+σ2－σ1。两探头之间超声波真实飞行时间为t0=（Δt1+Δt2）/2，两探头接收延迟的差值为 Δσ12=σ1－σ2=（Δt1－Δt2）/2。

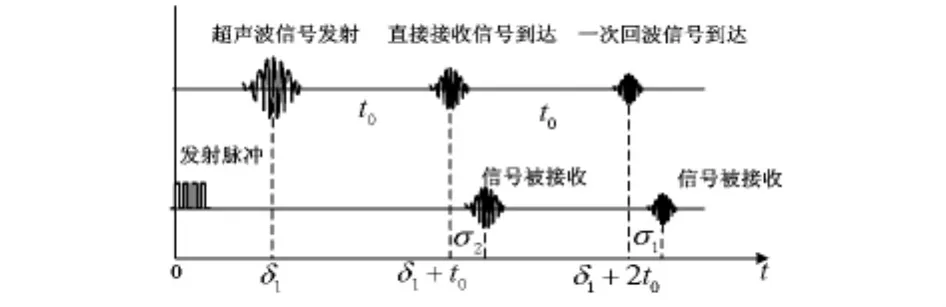
图2 双向回波法示意图Fig 2 Diagram of bi-echo method

利用双向回波法可以确定超声波信号在零流动下的真实传播时间t0。将上述过程中获得的直接接收信号在时间轴上左移t0，即可获得进行时间测量的参考信号。

3 飞行时间测量系统

基于双向回波法的超声波流量计飞行时间测量系统由硬件平台和软件模块构成。硬件平台包括进行声电信号转换的超声波探头、超声波发射电路、超声波接收放大电路、带通滤波电路、Arm控制和AD采集;软件模块包括采集卡设置、采集显示、数据存储和处理等。

测量系统的外部构造示意图如图3所示。发射电路对Arm控制器产生的短时脉冲进行电平转换，由于引入了继电器作为多路开关，图示的2只传感器只配备一个发射电路以减少硬件成本。每个探头配备有一个接收电路对接收到的超声波信号进行前置信号处理，包括放大和带通滤波。模拟开关作为多路选择开关将指定探头的信号输入到A/D转换器中，转换后的数字超声波信号在计算机中进行后续的数字信号处理。在系统时序上，Arm控制器和AD转换器共用一个系统时钟，Arm控制器利用时钟分频信号产生激励脉冲信号和系统的时序控制信号，包括发射选择信号、接收选择信号和A/D触发信号。软件模块安装在计算机上，主要用来执行测量算法，实现对超声波飞行时间的精确测量。

4 实验

在搭建的系统上利用双向回波法的标定方法和飞行时间测量方法进行了测量实验。传感器被频率为125 kHz的短时脉冲驱动，两传感器之间的距离分别固定在200，300，400，500mm。AD采样率为5MHz，每个固定距离处，分别进行50次重复实验。

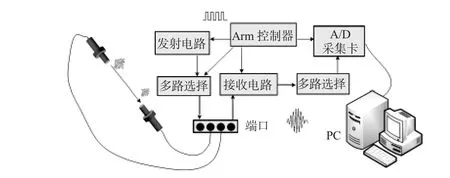
图3 测量系统外部构造示意图Fig 3 External structure diagram of measurement system

表1所示为标定实验的结果。SNR1和SNR2分别为采集的直接接收信号和一次回波信号的信噪比。

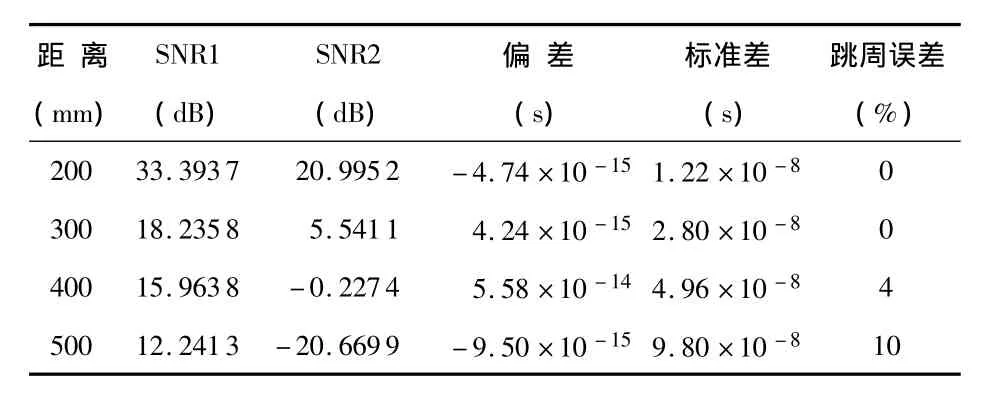
表1 标定实验结果Tab 1 Calibration experiment results

由上表可以看出:随着主探头距离的增大，所采集到的超声波信号的信噪比逐渐减小，所测时间的标准差逐渐增大，其偏差没有呈现出明显的规律。当主探头距离增大造成信号信噪比降低到一定程度时，跳周误差开始出现。表1显示标定精度能达到几飞秒至几十飞秒。

表2所示为飞行时间测量实验的结果。此处，SNR1和SNR2分别为参考信号和直接接收信号的信噪比。

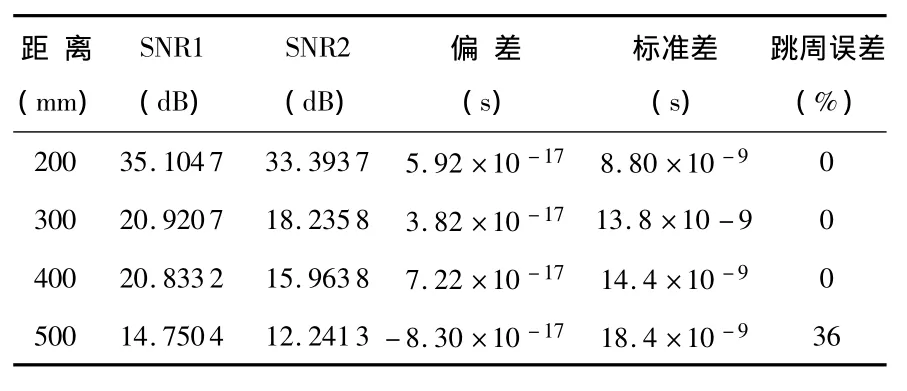
表2 飞行时间测量实验结果Tab 2 Time-of-flight measurement experiment results

上表显示测量实验的单次测量精度能达到8．8 ns。在采集信号的信噪比低至12．2413 dB时，单次测量精度仍能够达到 18．4 ns。

5 结论

本文搭建了基于超声波气体传感器的飞行时间测量系统。提出“双向回波法”的标定方法和一种适用于噪声环境的飞行时间测量方法。实验表明:标定精度能达到fs级，时间测量方法的单次测量精度能达到ns级。本文系统能保证飞行时间测量的可信赖性，并能够在低信噪比情况下获得较好的测量精度，可以应用于距离、流量和风速测量等领域中。

［1］ Wallace D R，Korba J M，Matson J E，et al．Intervalometer time measurement apparatus and method:US，4515021［P］．1985—05—07．

［2］ Bradshaw J E，Pedersen N E．Acoustic flowmeter with envelope midpoint tracking:US，4480485［P］．1984—11—06．

［3］ Eren H，Lowe A M，Basharan B．Processing ultrasonic signal to identify fluid contents in transit-time flowmeters［C］∥IEEE Instrumentation and Measurement Technology Conference，2002:1491－1495．

［4］ Wang B X，Zhang J．FPGA-based high-precision measurement algorithm for ultrasonic echo time of flight［J］．Journal of Measurement Science and Instrumentation，2010，1（2）:103 －107．

［5］ 张 涛，蒲 城，赵宇洋．传播时间法超声流量计信号处理技术进展述评［J］．化工自动化及仪表，2009，36（4）:1 －7．

［6］ Brassier P，Hosten B，Vulovic F．High-frequency transducers and correlation method to enhance ultrasonic gas flow metering［J］．Flow Measurement and Instrumentation，2001，12（3）:201 －211．

［7］ 邱立存，王汝琳．超声波气体流量测量系统的实现［J］．传感器与微系统，2006，25（1）:47 －49．

［8］ Grennberb A，Sandell M．Estimation of subsample time delay differences in narrowband ultrasonic echoes using the Hilbert transform correlation［J］．IEEE Transactions on Ultrasonic，Ferroelectric and Freqency Control，1994，41（5）:588 － 595．

［9］ Mandard E，Kouamé D，Remenieras J P，et al．Methodology for developing a high-precision ultrasound flow meter and fluid velocity profile reconstruction［J］．IEEE Transactions on Ultrasonic，Ferroelectric and Frequency Control，2008，55（1）:161 －172．