无人机测控链路中双混沌直序扩频技术的应用

付 民，茹 乐

（空军工程大学航空航天工程学院，陕西西安 710038）

0 引言

进入21世纪以来，随着科技的进步，无人机的应用范围也越来越广，特别是在军事领域。按功能划分，无人机系统主要由四部分组成:飞行器系统、测控系统、任务设备系统、后勤保障系统［1］。其中，测控系统又可以分为测控链路、指挥控制站及机载通信设备3个部分。无人机测控链路实现的是无人机和地面控制站的数据收发，是整个无人机系统的“神经中枢”，是连接着无人机和地面控制站的生命线，需要极高的安全性。在条件允许的情况下，要求链路中通信的可靠程度达到99%［2］。但是，由于无人机飞行阶段复杂多变的环境，使得通信的可靠性程度受到极大的挑战，因此，研究无人机测控链路的抗干扰技术是十分必要的。同时，为了满足无人机一站多机或一机多站以及军事通信保密性的需求［3］，也需要提高无人机链路的多址能力和抗截获能力。

目前，直接序列扩频是一种最常见的运用在无人机测控链路中的抗干扰技术［4］，但是传统直扩系统中所采用的序列如m序列、gold序列普遍存在着数量有限、复杂度低、保密性不高的缺点［5］，使得系统性能存在一定缺陷。混沌序列相关特性好，还具有隐蔽性强、数量众多等优点，是一种十分优良的伪随机序列［6］，被普遍认为是第三代移动通信DS/CDMA扩频序列的理想地址码［7］。本文在对直接序列扩频和混沌序列进行研究的基础上，对直接序列扩频系统进行了一些改进，提出一种新的双混沌直接扩频技术，并通过Matlab仿真工具对其进行建模仿真研究。

1 双混沌直序扩频技术

1．1 混沌序列

混沌是非线性科学研究的中心内容之一，与相对论、量子力学一起被认为是20世纪物理学的三次重大革命，是当今前沿的研究课题［8］。混沌系统所特有的伪随机性、确定性和对初始条件的敏感性，使之能够产生数量众多的混沌序列。同时，混沌序列并非随机却貌似随机，具有复杂性和不可预测性，这些使它具有天然的隐蔽性，非常适合于保密通信。混沌序列近年来被广泛应用于扩频通信系统中，大大增强了系统的多址能力和抗截获能力。

这里简要介绍几种传统的混沌映射，并对其一种混沌序列的相关特性进行仿真。

1）Logistic混沌映射［9］:Logistic混沌映射是一种被广泛研究的混沌映射，其表达式为

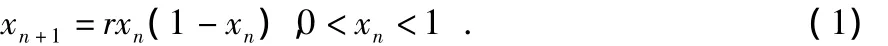
式（1）中，只要当3．5699456≤r≤4时，就会工作在混沌状态 ，序列的均值为0．5。

2）Tent混沌映射［9］:Tent混沌映射的表达式为

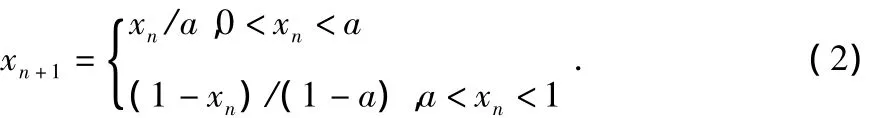
其中，0＜a＜1，序列的均值为0．5。

3）Chebyshev混沌映射［9］:w阶 Chebyshev混沌映射表达式为

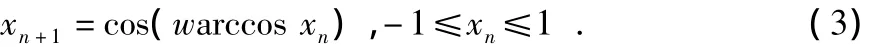
通常，w为2的整数次幂，序列的均值为0。

根据Chebyshev映射的定义，取初始值分别为－0．38000，－0．38001，w=2。产生两条码元长度为1000的混沌序列，在Matlab下做相关特性仿真，结果如图1，图2所示。

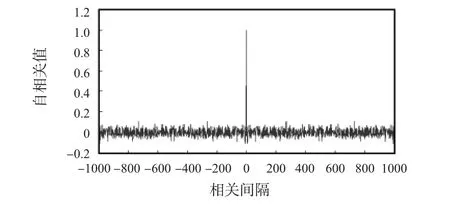
图1 基于Chebyshev混沌序列的自相关系数（N=1000）Fig 1 Autocorrelation coefficient based on Chebyshev chaotic sequence（N=1000）

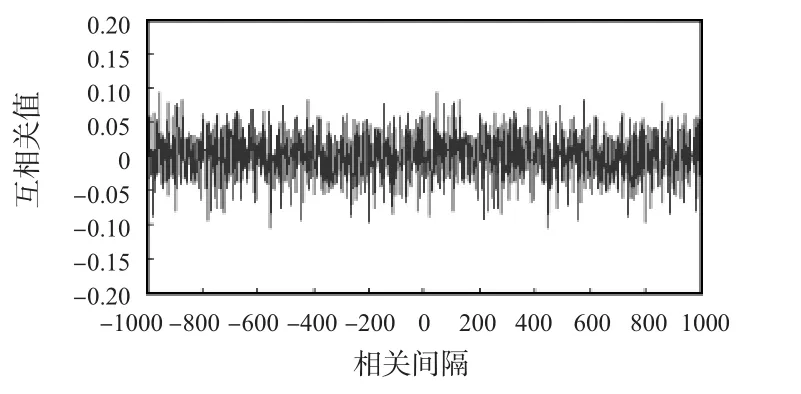
图2 基于Chebyshev混沌序列的互相关系数（N=1000）Fig 2 Cross-correlation coefficient based on Chebyshev chaotic sequence（N=1000）

从图1中可以看出:Chebyshev混沌序列自相关峰非常尖锐，有一个主瓣为1，其余旁瓣非常小，接近于0，自相关特性很强。

从图2中可以看出:Chebyshev混沌序列的互相关值非常小，接近于0，具有良好的互相关特性。

以上仿真表明:混沌序列是一种非常优良的伪码序列，同时，在初值仅相差0．000 01的情况下，经过1 000次不断地迭代运算后，能够产生2个互不相关的伪随机序列。利用这一特点，通过设置不同的初值，可以得到数量庞大的混沌序列，适用于多址通信。

1．2 双混沌直序扩频

双混沌直扩组成框如图3。

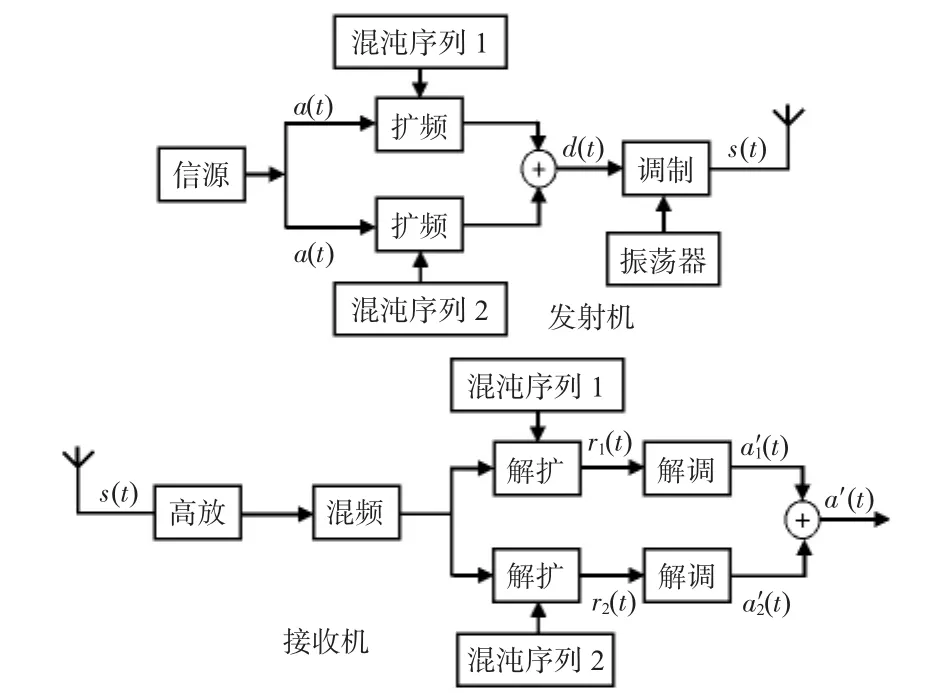
图3 双混沌直序扩频组成框图Fig 3 Composition block diagram of dual chaotic direct sequence spread spectrum

假设发射端的数字基带信号为a（t），经两条混沌序列g1（t），g2（t）扩频处理后，得到信号d（t）

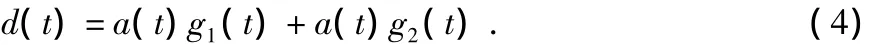
假设载波为cosωt，则经过BPSK调制后的发射信号s（t）

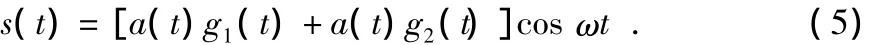
信号经信道传输到接收端，分别与本地产生的混沌序列g1（t），g2（t）相乘，得

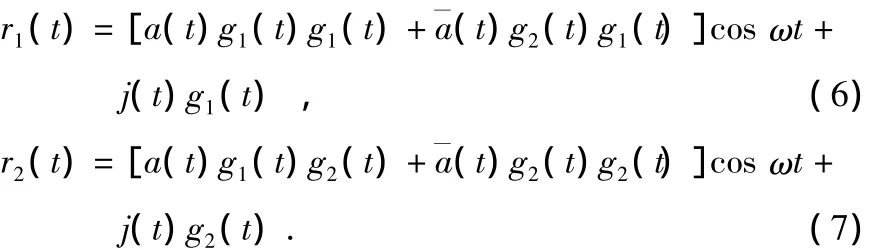
最后，经过包络检波后，得到的输出信号为

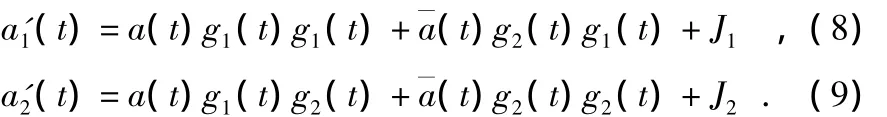
干扰经过扩频处理后，谱密度大大降低，频谱特性基本一致，后又通过滤波和包络检波处理，两者近似相等，可以得到J1≈J2。而且由于混沌序列互相关系数远小于1，完全同步时，自相关系数为1，由此可以近似得到

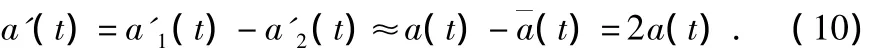
在系统的整个处理过程中，将有用信号看作为差模型号，将干扰、噪声等无用信号看成共模信号，在扩频、解扩处理后，最后将两路信号进行差模运算，可以有效地抵消噪声，增强有用信息，系统性噪比增大，从而提高了系统的抗干扰能力。

2 仿真结果分析

这里采取Matlab仿真软件进行建模仿真。简化系统模型，假定系统为单用户，扩频码长为127，仿真当中没有考虑码片速率fc，默认为1，信噪比变化范围为［－30，10 dB］，以2 dB速率递增。在高斯白噪声信道的情况下，加入不同类型的干扰信号，在不同的信噪比（信干比）条件下，对传统直序扩频和双混沌直序扩频进行误码率仿真。

2．1 高斯白噪声下的仿真结果

传统直序扩频和双混沌直序扩频在高斯白噪声信道下的误码率仿真结果如图4所示。从结果中可以得到，在高斯信道条件下，双混沌直序扩频的误码率要小于传统直序扩频，在信噪比为－15 dB时，传统直序扩频的误码率为7．35×10－4，而双混沌直序扩频的误码率为0。在无干扰的条件下，双混沌直序扩频的性能要优于传统直序扩频。

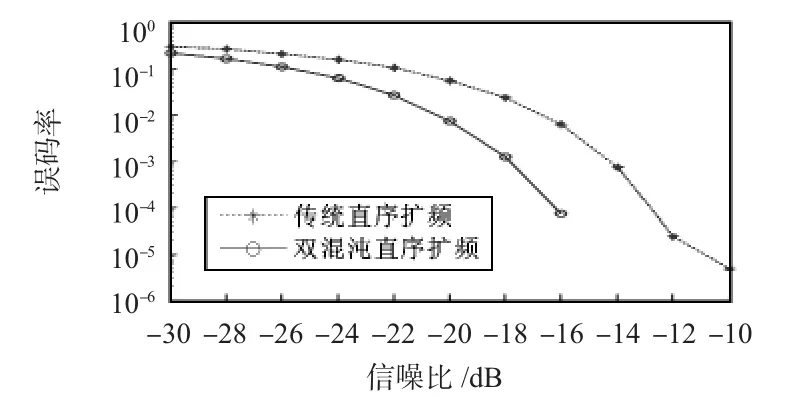
图4 高斯白噪声下系统误码率比较Fig 4 Comparison of system bit error rate under Gaussian white noise condition

2．2 部分频段干扰下的仿真结果

在高斯白噪声信道下，加入部分频段干扰。仿真中，部分频段干扰的频带只占传输频带的一部分，并服从高斯分布，信噪比保持不变为0 dB，信干比变化范围为［－40，－10 dB］，以2 dB速率递增。仿真结果如图5所示。可以看出，双混沌直序扩频的误码率要小于传统直序扩频。在信噪比为－22 dB时，双混沌直序扩频误码率为5×10－5，而传统直序扩频误码率为2．6×10－4。在部分频段干扰的条件下，双混沌直序扩频的性能要优于传统直序扩频。

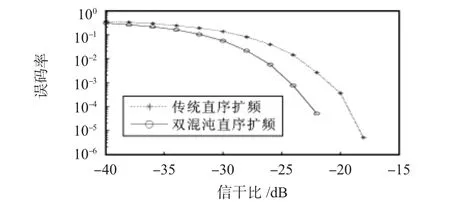
图5 部分频段干扰下系统误码率比较Fig 5 Comparison of system bit error rate under partial-band interference condition

2．3 单频干扰下的仿真结果

在高斯白噪声信道下，加入干扰信号i（n）=Acosn。仿真中，信噪比保持不变为0，通过调整干扰噪声幅值A值来调节信干比，信干比变化范围为［－30，－10 dB］，以1 dB速率递增，得到结果如图6所示。可以看出，信噪比在－26 dB以下情况下，两者误码率相差不大，但在误码率在－26 dB以上的时候，双混沌直序扩频的误码率远小于传统直序扩频，在两者误码率都为5×10－6时，双混沌直序扩频要优于传统直序扩频8～10 dB。在单频干扰的条件下，双混沌直序扩频的性能要优于传统直序扩频。

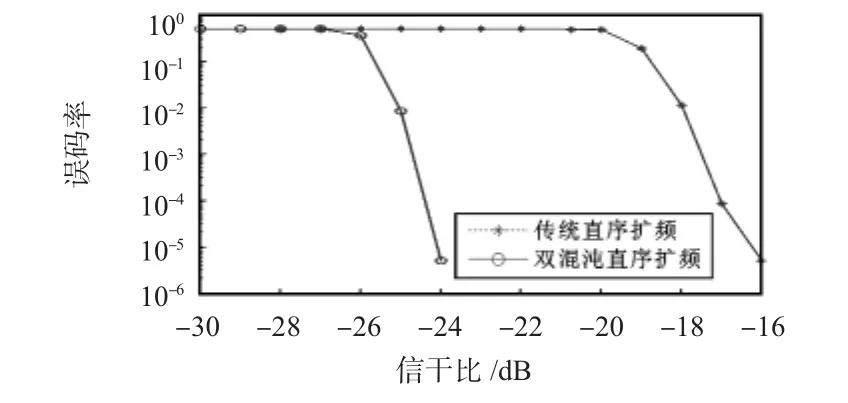
图6 单频干扰下系统误码率比较Fig 6 Comparison of system bit error rate under single-frequency interference condition

3 结论

本文立足无人机测控链路抗干扰能力强，隐蔽性好，多址能力强的需求特点，对混沌序列和现今无人机链路中应用最广泛的直接序列扩频技术进行深入研究，在此基础上提出一种全新的双混沌直序扩频技术。通过建立仿真模型验证，该方法能有效提高测控链路的抗干扰能力，同时，由于混沌序列复杂度高，数目众多等优点，测控链路的抗截获能力和多址能力也能得到进一步提高。

［1］ 仵敏娟．无人机数据链的关键技术研究［D］．西安:西北工业大学，2007．

［2］ Edrich M，Schmalenberger R．Combined DSSS/FHSS approach to interference rejection and navigation support in UAV communication and control［C］∥IEEE 7th Int’l Symp on Spread-Spectrum Tech ＆ App1，2002:687－691．

［3］ 吴 潜．无人机测控系统的现状与发展趋势［J］．电视技术，2009（9）:90－94．

［4］ 李思佳，毛玉泉，郑秋荣，等．UAV数据链抗干扰的关键技术研究综述［J］．计算机应用研究，2011（6）:2020－2024．

［5］ Kurian A P，Puthusserypady S，Su Myat Htut．Performance enhancement of DS/CDMA system using chaotic complex spreading sequence［J］．IEEE Transactions on Wireless Communications，2005，4（3）:984 －989．

［6］ 张 怡，费恒歌，赵恒斌，等．混沌序列相关特性研究及在扩频通信中的应用［J］．火力与指挥控制，2011（11）:19－24．

［7］ 李长庚，周家令，孙克辉，等．四种数字混沌扩频序列的平衡性分析［J］．计算机应用，2008，28（1）:95 －97．

［8］ 王兴元．混沌系统的同步及在保密通信中的应用［M］．北京:科学出版社，2012．

［9］ 虞 闯，丁晓东，于舒娟．三种混沌扩频序列性能研究与分析［J］．沈阳理工大学学报，2011（1）:21 －24．