基于模糊神经网络PID算法的电阻炉温控系统

董爱华,李梦瑶

0 引言

电阻炉不仅在工业生产中非常广泛的应用于冶金、机械、建材等行业[1][2]，而且在科研、教学中也有应用,它的温度控制的优劣直接影响产品的品质[3]。

现阶段，对电阻炉采用的主要控制方法是PID控制[4]，还有一些采用模糊控制和神经网络控制。PID控制的控制参数一旦确定，便无法改变，对电阻炉这种时变的控制对象控制效果不是很好。当采用模糊算法时,模糊系统学习能力较差，模糊规则的建立和隶属度函数的生成和调整较困难，模糊控制消除静态误差的能力较差,难以达到较高的控制精度[5]。当采用神经网络控制时，不能利用现有的知识,无法引入人工经验，不能依据已有的控制经验来解决控制问题。

本文把三个控制算法融合起来，形成模糊神经网络PID算法，兼有三种控制算法的优点，经仿真表明，该算法对电阻炉温度的控制动静态性能较好。

1 电阻炉模型

电阻炉温控系统的简图如图1所示：

图1 电阻炉温控系统简图

通过改变一个周期内晶闸管的通断时间，改变电阻炉的电压，从而改变电阻炉的功率，使实际温度跟随设定温度的变化而改变。

2 电阻炉模型

理论分析和实验结果证明，电阻炉在阶跃输入影响下，具有非振荡特性和自平衡能力，可用比例环节、一阶惯性环节和一个延迟坏节来近似。其传递函数可以近似地表示成：

其中K—静态增益，τ—纯滞后时间，T—惯性时间常数。

3 模糊神经网络PID控制器的设计

当|e(k)|＞ ε，(ε的大小决定着控制精度，ε越小，控制精度越高，程序越复杂；反之，ε越大，控制精度越低，程序越简单)说明误差较大，控制器按最大或最小输出，具体到电阻炉温度控制，即温度误差较大， 控制器以最大或最小输出，电阻炉全功率或功率为零，也就是控制电阻炉电压为最大或零。当|e(k)|<ε,系统采用模糊神经网络PID控制。在实际应用中，根据不同控制精度的要求，多次调试，选择合适的ε。

本文提出的模糊神经网络PID控制器的结构，如图2所示：

图2 模糊神经网络PID控制器的结构图

模糊神经网络PID主要有两个部分组成（1）传统的PID控制器。这是控制器的核心，PID控制器对被控对象直接进行闭环控制，模糊神经网络主要作用是实时调节PID控制器的参数,从而达到最好的控制效果。它的最大特点是控制参数Kp、Ki、Kd是实时改变的。（2）模糊神经网络FNN，根据系统的实时运行状态，即根据误差和误差变化率来调节PID控制器的参数，使控制指标达到最优[6]。

本文中的PID控制并不是简单的比例、微分和积分的“线性组合”关系[7]，若想取得较好的控制效果，必须使比例、积分和微分3种控制作用达到最佳的组合。模糊神经网络的主要任务就是利用模糊神经网络理论建立误差e(k)、误差变化率ec(k)和PID控制器的3个参数Kp、Ki、Kd的关系。

如公式（2）

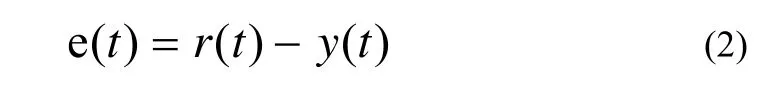
e(t)—t时刻的采样误差;y(t)—被控对象t时刻的实际输出：r(t)—t时刻的设定输出：t—采样时间。

3.1 PID控制原理

控制器采用的最多的是PID控制，PID控制是一种线性控制方法，原理框图如图3所示。其位置式控制规律，如图3所示：

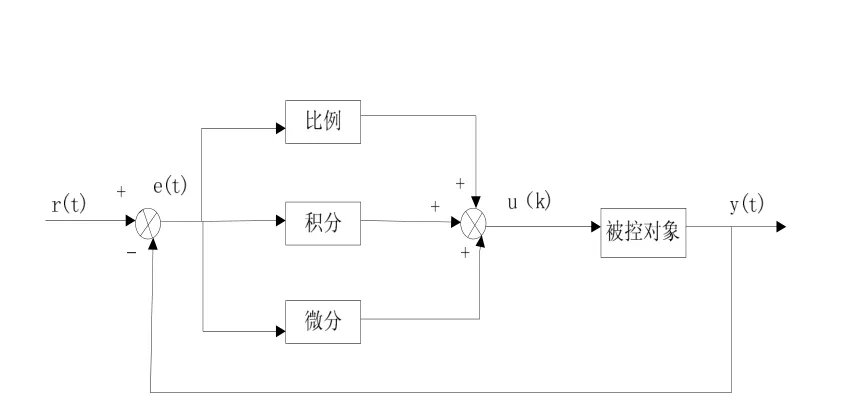
图3 PID控制系统原理框图

如公式（3）

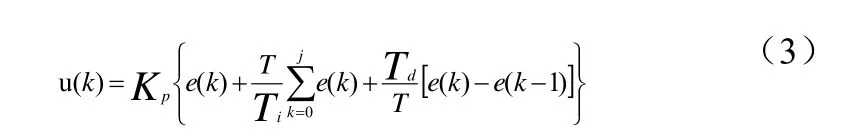
其中u(k)—第k次采样时刻控制器输出的控制量；Kp—比例系数;Ti—积分时间常数；Td—微分时间常数；T采样周期；Ki=Kp/Ti为积分系数，Kd=KpTd为微分系数，e(k)和e(k-1)分别是第k和k-1次采样时刻输入误差值。

3.2 模糊神经网络的结构和设计

模糊神经网络（FNN）将神经网络的学习能力引入到模糊系统中，将模糊系统的模糊化处理、模糊推理通过神经网络来表示[8]，一般分为四层：1 输入层；2 模糊化层；3 模糊推理层；4 输出层。它的结构图，如图4所示：

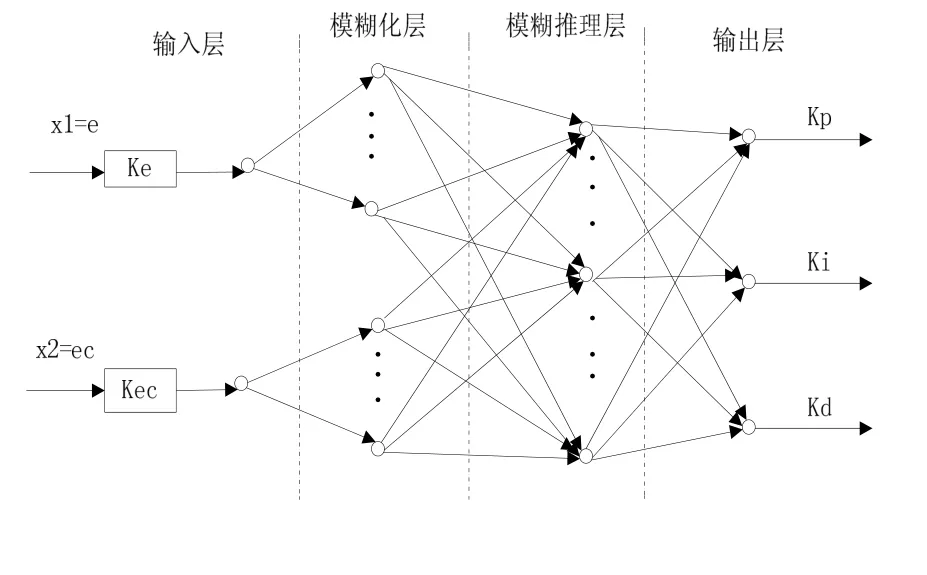
图4 模糊神经网络结构图

输入层与模糊化层、模糊化层与模糊推理层之间的连接权值均为l，只有模糊推理层与输出层之间的权值需要调整。

本文中的模糊神经网络是2-6-9-3结构，两个输入神经元，3个输出神经元分别对应PID控制器的3个参数Kp、Ki、Kd。

模糊神经网络各层的输入输出关系如下：

第1层（输入层）：作用将输入量导入网络，如公式（4）

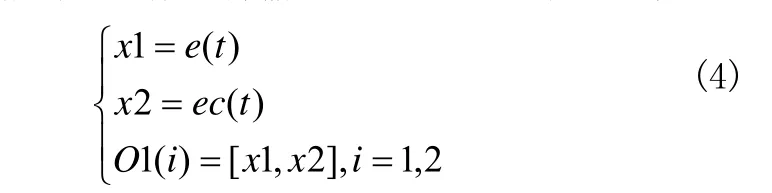
第2层（模糊化层）：将输入变量模糊化，计算输出各输入变量属于各语言变量的隶属度函数。本层有6个节点，分别对应误差和误差变化率的语言变量:B(大),M（中）,S（小）。语言变量的个数的选择和系统的复杂程度和控制精度的要求有关。控制精度要求高，系统复杂，选择的语言变量个数就要多，如公式（5）

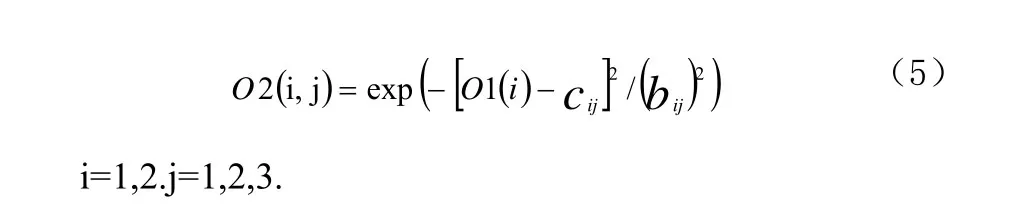
模糊化层采用高斯型函数作为隶属函数,cij和bij分别是隶属函数的中心值和宽度。

第3层（模糊推理层）：

由输入变量个数N=2，每个变量的模糊子集数为M=7，根据y=MN,可得此层的节点数m=9[9]。

第4层（输出层）：

ωij是模糊推理层与输出层之间的权值。三个输出神经元的输出为PID控制器的三个参数Kp、Ki、Kd。

3.3 模糊神经网络的学习算法

系统的目标函数：

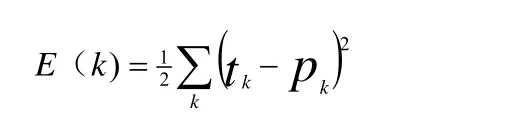
tk第k个神经元的期望输出， pk第k个神经元的实际输出。

模糊神经网络的高斯函数的中心cij和宽度cij，及模糊推理层与输出层之间的权值ωij采用BP的梯度下降法。

η为学习速率，α为惯性系数。

4 仿真结果与分析

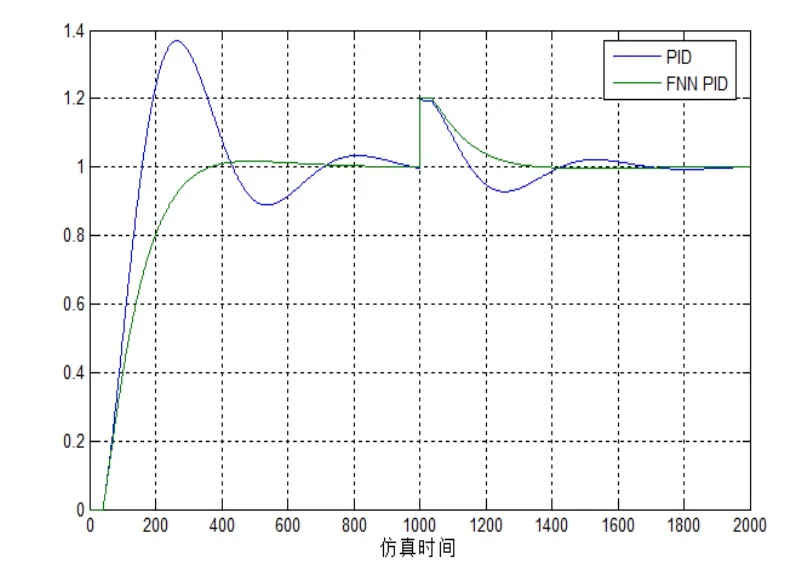
图5 仿真曲线图

从仿真曲线可知，模糊神经网络PID（FNN PID）和PID比较：模糊神经网络PID上升速度快，超调量基本为零，在加入外部扰动时，能快速的调节到稳定。

[1]邢伟.电阻炉智能模糊控制系统的研制[D].杭州: 浙江理工大学,2008.

[2]谢铮辉,马有良,邓琥等.基于PID的电阻炉炉温控制系统[J].化工自动化及仪表,2011,38(8):931-933

[3]孙凯,李元科.电阻炉温度控制系统[J].传感器技术,2003,22(2):50-52.

[4]马雪峰,田跃辉，李玲莉.一种改进PID控制算法在电阻炉温度控制系统中的应用[J].船海工程,2009,38(2):68-70.

[5]李英顺 ,伦淑娴.模糊PID温度测控仪[J].仪表技术与传感器,2003,(1):20-22

[6]张妤.基于知识的模糊神经网络PID控制器的研究[D].哈尔滨：哈尔滨理工大学，2006.

[7]王彦，邓勇，王超.基于改进粒子群算法的模糊神经网络PID控制器设计[J].控制工程，2012,19（5）：761-764.

[8]刘敏，马军爽.模糊RBF 神经网络在锅炉水位控制中的应用[J].微计算机信息, 2006 ,22 ,（9-1 ）：56-58.

[9]刘莉，张彦敏.基于改进遗传算法的FNN PID控制器在温度控制系统中的应用[J].工业控制计算机，2009，22（3）：63-65.