基于二叉树模型的风险投资项目价值评估
吴 琦
(西安文理学院 商学院,西安 710065)
0 引言
二叉树期权定价模型之所以被广泛应用于风险投资项目的评估,有以下几个原因:第一、它将风险中性的概念融入了整个定价过程,而结论确实可以应用于其他非风险中性环境的;第二、它将投资预期收益的连续的变化看作是离散的随机游走过程,用完全透明的方式处理预期收益和期权价值的运动过程;第三、尽管二叉树模型的收敛速度较慢,但是它的极限还是趋于B-S期权定价模型的。二叉树期权定价模型被广泛应用于风险投资项目的评估,但模型较为传统,每一阶段都以“二叉”的形式出现,不能反映真实投资过程中多种选择权的状态,带来评估结果较大的误差。所以本文试图引入“多叉”的思想:即一个完整的投资过程各阶段所面临的实际情况是不同的,因此可供其选择的途径也是不同的,将二叉树、三叉树甚至混合使用在模型中,给决策者提供灵活和真实的方法选择。
1 利用树形结构求解期权价值——二叉树模型
1.1 风险中性假设
风险中性原理是由J.Cox、S.Ross在1976年推导期权定价公式时提出的,该原理与投资者的风险偏好并无关系,因此推广到对任何衍生证券都适用。所以人们在这之后的衍生证券定价推导中,逐渐接受了这样的前提条件,就是所有投资者都是风险中性的,或者是在一个风险中性的经济环境中决定价格,并且这个价格的决定,又是适用于任何一种风险偏好的投资者。风险中性假设下得到的衍生品估值同样可以应用于非风险中性的世界。真实世界里的投资者尽管在风险偏好方面存在差异,但当套利机会出现时,投资者无论风险偏好如何都会采取套利行为,消除套利机会后的均衡价格与投资者的风险偏好无关,罗斯在1976年严格证明了这一逻辑。
1.2 二叉树模型
单步二叉树模型是二叉树模型的基础,它只反应一个阶段的资产的变化状况。我们可以假定标的资产的价格为S0,对应的期权价格为 f0。假定期权的期限为T,在期权有效期内,股票价格可能有两种趋势:一种是由S0上升为S0u,其中u>1为上升参数;另一种是由S0下降至S0d,其中0<d<1为下降参数。因此,当股票价格上涨时,增长的比率为u-1;股票价格下跌时,下跌的比率为1-d。假设如果股票的价格变动到S0u,相应期权的价格为 f0;如果股票的价格变动到S0d,相应期权的价格就为 fd。
如果考虑一个由α只股票组成的股票多头和一份期权空头所组成的资产组合。此时可以表示α为对冲比例,也即是卖出一份买权所必需买入的股票的股数满足风险中性假设,我们假定该组合没有风险,也就是可以认为其收益率就等于无风险利率,那么就可以构造出该资产组合的成本,并由此来计算期权的价格。若股票价格上升,那么期权到期日时该资产组合的价值为S0uα-fu;若股票价格下跌,则资产组合价值为S0dα-fd。为了使组合不存在任何风险,令上述两式相等得到:
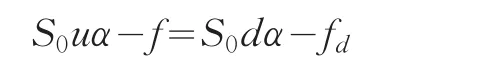
由于此时该组合是无风险的,其收益率就应该等于无风险利率。设无风险利率为r,则资产组合的价值的贴现值为
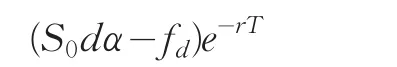
若使资产组合的初始成本与之相等,便得到
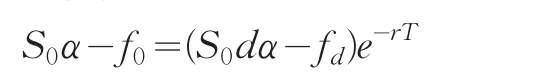
解得上一个期权的价格为
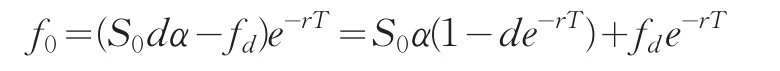
此时可得

讨论当上涨的概率为p时,股票的收益期望为
E(S)=PS0u+(1-P)S0d=PS0(u-d)+S0d
这说明了股票价格实际上是按照固定的无风险利率稳定增长。所以股票的收益率为无风险利率与股价上涨的概率为P是相同的概念。
当二叉树从两步开始,一些参数将随之发生变化。对于单步二叉树模型,贴现的期限即为期权的期限T,两步二叉树模型开始,各步价值贴现的期限可以步长的概念来代替。这里不妨假设各步步长相等,均为ΔT年。在这样的假设下,前面推出的期权价格公式变为
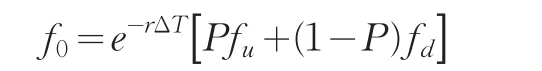
其中 P=erΔT-d/u-d 。
重复运用该式向前推导得出两步二叉树模型的期权现值
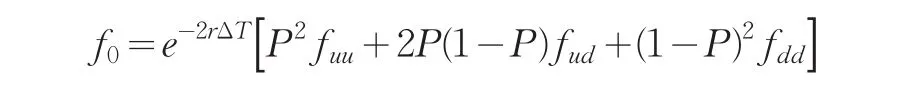
当推导n步二叉树模型的通式时,采用的是向前倒退的方法来为期权定价,也就是从期权的定价日始,在每个时间点iΔT的期权价值都可以由时间点(i+1)ΔT的价值通过贴现其期望价值来得到。利用数学归纳法推导出n步二叉树的期权现值为:
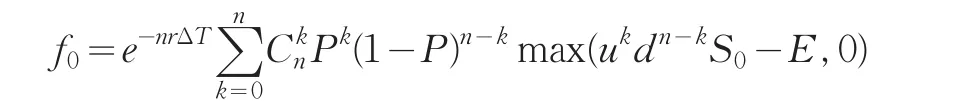
下面对公式进行化简:
(1)当ukdn-kS0<E 时
max(ukdn-kS0-E)=0
则 f0=0,期权无价值。
(2)当ukdn-kS0>E时,就可以去掉0项而取正项:
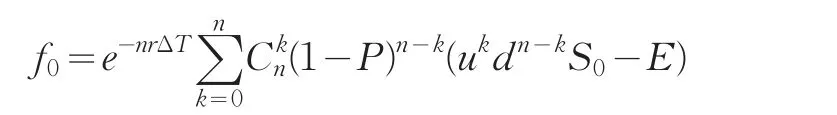
由于序列Ak=Pk(1-P)n-k(ukdn-kS0-E)为递增序列,则必然存在一个最小整数w使得当k≥w时ukdn-kS0>E ,即去掉式中的0项得到
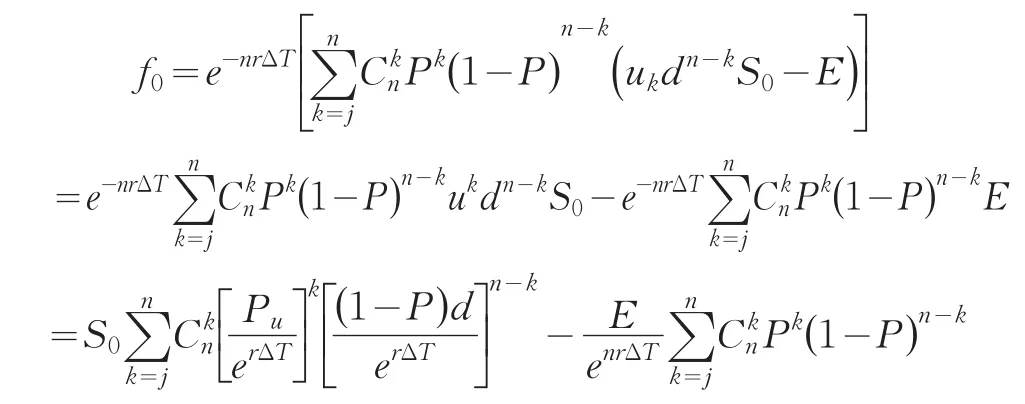
将通式化简至此,就会更容易观察出整个期权价值的成分,我们可以把他们分为标的资产价值的运动部分和每一期对应行权价格的贴现价值部分。每一时点的行权价格部分由该节点向后延伸出的所有状态步步贴现而得。
1.3 对二叉树模型分析的总结
在实际中,二叉树的收敛速度并不理想,这是一个只有在保证了无穷计算的情况下才会得出最精确结果的结论。如果一个分析员仅仅假定在期权期限内价格变化只由一步或几步二叉树来表达,则由此得出的期权价格将会是一个非常粗略的近似值。降低误差的办法之一是提高步数或尽可能缩小步距ΔT,但是步数的增长所带来的运算的复杂程度是呈现指数化增长的。在实际中应用二叉树时,期权的期限可能会被分割为30或更多的步数。在每一个时间步,资产价格的变动都由一个单步二叉树来表达。那么在30个时间步中,总共有31个终端的股票价格,即230,大约10亿种可能的资产价格变动路径。在步数达到一定程度的时候,除了使用数学归纳法来推导可能的定价公式,数值解就只有通过数学软件来实现。
2 三叉树期权定价模型
2.1 构建模型
能够降低二叉树模型误差的另一种方法是增加自由度——也即每一步可能的状态,比如将二叉树推广至三叉树。最早提出这种思想的是Kamrad B.和Ritchken P.,他们在1991年发表于Management Science上的一篇论文中提出设想,通过增加每一期可能的状态来提高最终计算的精度。Boyal P P.将其扩展成为三叉树模型,每一期存在三种可能的状态:上升、不变和下降,并且上升和下降两种状态是对称的。Tian Y.重点研究了三叉树模型,同时仿照二叉树模型的风险中性世界假设,推导出了三叉树模型的风险中性概率,形式为时间ΔT的指数函数。
从二叉树期权定价公式推导过程看出,美式期权每一期都必须对期权价值和内在价值进行比较,所以可先从欧式期权入手,推导三叉树模型对应的经验公式。在建立三叉树模型之前先进行一系列前提假设:
(1)假设市场是完备的,所有投资者信息共享;
(2)市场是无摩擦的,也就是不存在税收和交易费用;
(3)市场中不存在套利机会;

其中r为无风险利率,δ为瞬时波动率,dz为标准维纳过程。这表示S下一瞬间的运动增量为dx,这个增量来自于两个部分,第一部分是确定项,第二部分是随机项。考虑应用Ito引理的随机微分方程,第一步将连续的S(t)离散化,把[0 , T ]分割为间距相等的n个部分,每步的长度ΔT=T/n,在任一步时段[t,t+ΔT] 中,资产价格的变动服从于=rΔT+δΔz,因此 S 的数学期望就表示为E(S)=SerΔT。再由Ito引理二阶和三阶随机微分方程,S2和S3在[0,T]上分别服从于随机方程
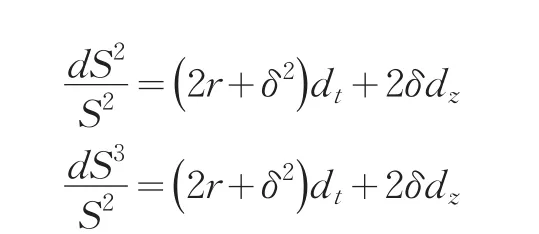
分别离散化之后可得
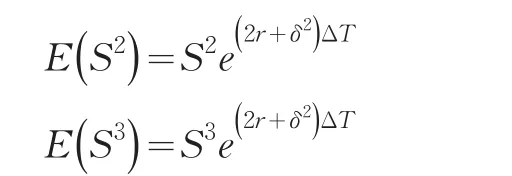
现在考虑三叉树定价模型的建立,类似于二叉树模型,首先分析单步的三叉树。假设在t0时刻,标的资产价格为S0,经过时间T后,可能的运动状态有三种:上升至S0u、下降至 S0d,以及维持初始的 S0不变,其中u>1>d>0。
这里为了方便迭代,得到适用于有限可数步三叉树期权定价的通项公式,假设该标的资产的价格有序运动之后的结果与运动过程无关,用式子表达为u·d=1。即是说S0开始经过先上升后下降或经过先下降后上升,效果一致,会到达同一个位置。任一节点St经过任意一步距离的运动,先上升后下降、先下降后上升与水平运动,最终达到的状态相同,这样假设的好处是每一期只增加有限个新节点,使得节点数不致以指数倍增长。
如果假设S0向上和向下以及保持不变的概率分别Pu、Pd和 Pm,则必有Pu+Pm+Pd=1。
同时,为了有效控制每一步的节点数,可做出假设使得部分节点可以重合,向上和向下的路径和先后顺序与最终的结果无关,学术界比较常用的办法添加限制性条件

将Pu、Pm和Pd分别看作是S0向上、向下及保持不变对应的权数,即得出S、S2和S3的数学期望,由此得到方程组包含5个独立方程,此时求解Pu、Pm、Pd、u和d这五个未知数后将Pu、Pm和Pd项通过u和d表示
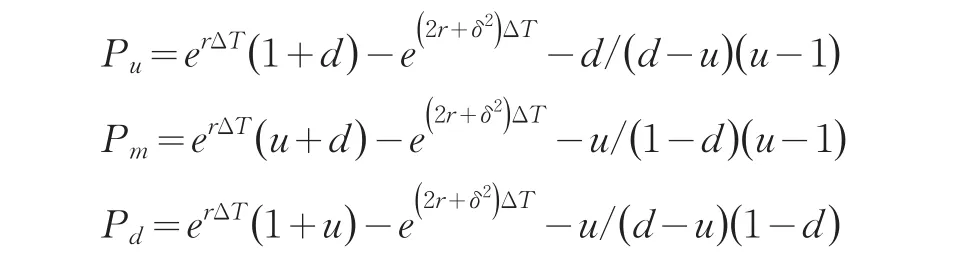
方程组的解只包含r、ΔT
与二叉树求解的思路相同,首先按树形将资产价格向后推至尾节点,再利用贴现逐步向前推,即从期权定价日开始向前倒推,在时刻iΔT的期权价格可以从下一时刻(i+1)ΔT的期权价值贴现期望价值得到,用表达式描述就是
f(SΔT,iΔT)=e-rΔT[Pu·f(u·SΔT,(i+1)ΔT)+Pm·f(SΔT,(i+1)ΔT)+Pdf(d·SΔT,(i+1)ΔT)] 其中f(SΔT,iΔT)为iΔT时刻的期权价格,f(u·SΔT,(i+1)ΔT)、f(u·SΔT,(i+1)ΔT)和 f(SΔT,(i+1)ΔT)则分别代表资产经过ΔT时间,以u的变动幅度上升,以d的变动幅度下降以及保持不变后对应的期权价格。类似于二叉树模型,利用数学归纳法可以推导出多期期权价格的估算公式
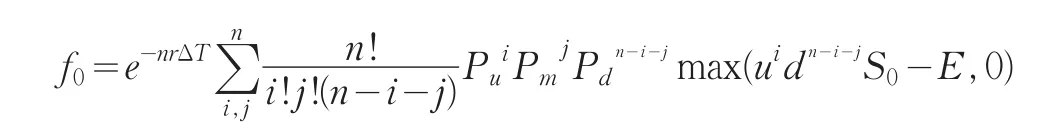
2.2 敏感性分析
2.2.1 基本原理
敏感性分析是非常常用的一种不确定性分析方法,是利用现代化的数据处理工具或软件模拟一个或多个不确定性因素变动一定幅度所带来的决策评价指标的变动程度,据此判断各种不确定性因素的变化对实现最终的决策目标的影响程度,以期在纷繁的外部环境发生不利变动时及时做出反应,对最大的风险范围、承受能力给出合理的判断。
2.2.2 单因素敏感性分析
单因素敏感性分析又称为局部敏感性分析,它只考虑单一因素对结果的影响。它可用于寻找那些对目标值影响相对较大的单个因素。首先需要保证每个单因素之间相互独立;在此基础上假设其他因素不变,每次只对某一个单因素的变化和其对目标值的影响程度进行分析,借助图表表现二者的相关关系;处理采用“连环替代法”,即将其他假定不变的因素按照上述方式变动,变动比例和临界值都取相同来观察目标值的变化,直至取遍所有的不确定因素。
确定敏感性因素是有选择性的,从实际投资活动出发,以提供投资决策建议为目的的前提下,应优先选择那些有经济含义、可控可测的那些变量。假设有经济值表达式F=f(x1,x2,…,xn),确定敏感性因素为 x1,x2,x3,x4,那么整理数据后应该至少能从两个方面得出结论:
(1)敏感度系数。敏感度系数是指项目评价值相对于不确定因素的敏感程度。以敏感性因素x1为例,取x1的变化量为Δx1,对应经济值f的变化量为Δf,则该段该因素的敏感度系数S1=Δf/Δx2。若将敏感性关系在F-x1坐标轴上绘制成曲线,S1代表了连接两点的线段的斜率;若Δx1→0,则S1代表了曲线在该点的斜率。这些都是可以直观上从曲线的起伏程度上看出来的。
(2)临界值。F是有经济含义的,假定F为年利润率,x1为年经营成本。则利润率必须要保证在一定的范围之内,譬如必须使F≥0,那么相应的x1也必定会有一个范围,譬如计算出x1≤f(F),这个值就是该不确定因素的临界值。在实际的经营活动中,假设其他条件不变时经营者必须保证经营成本小于某一个确定的值才能使公司获取正利润。
仍取 S0=100,E=80,r=0.1,δ=0.25,ΔT=n=5,计算出的期权价值 f0可作为一个期望价值。之后开始分析各单因素变动后的取值。
为了分析方便,我们选定S0、E、r、δ、n为待验证的敏感性因素,每次变动一个因素,其他因素保持不变。最小变动单位的选定上,S0和E的基础数值较大,同样的变动比例下变动数值更大,因此设定其最小变动单位为±1%;r和δ设定为±5%。变动档均为上下10档,即每一个对比样本包含数据20组,绘制敏感性分析表后观察数据发现,r主要以一阶形式出现,而δ多以二阶和三阶形式出现。这就说明了期权的价值对δ的变动相对于r更为敏感,或者说通过同样幅度的变动,δ变动所造成的期权价值变动幅度更大。由于S0和S0之后的运动趋势代表了投资所能带来的现金流情况,S0的变化对于追加投资、延迟投资或者撤出投资是起决定性作用的,因此S0与期权价值是呈正向变动的;相反作为投资成本的E越大,与现金流收入相较的差距越小,利润获取空间就越小,导致期权价值的降低。因此E与期权价值是逆相关的。
2.2.3 多因素敏感性分析
多因素敏感性分析又称为全局敏感性分析,是对单因素敏感性分析的推广。即是说许多因素的变动趋势之间存在相关性,一个因素的变动将会带来其他因素的变动。在这样的假设条件下,只考虑单因素的敏感性就存在局限性。由于全剧敏感性分析需要考虑所有可能发生变化的因素各自变动不同幅度的多种组合,计算的过程会比普通的单因素敏感性分析困难得多,如果不确定因素小于3个,且目标函数计算简单,尚可结合解析法和作图法进行分析。本文的研究对象为超过3个的不确定因素,并且各自代表不同的含义,彼此之间相关性较弱,可认为其相互独立。因此全剧敏感性分析不作为本文的研究重点。
3 总结
本文基于当前国内风险投资势头日渐增强的背景,考虑到实务界盲目投资现象的存在,提出对风险投资项目进行合理的估值,为决策者提供建议。通过将实物期权引入风险投资项目,结合使用二叉树定价模型和三叉树定价模型对项目的不确定性部分进行价值评估,形成了可操作的一种不确定性项目估值的方法。对估值模型的研究,一方面要尽量提高估值结果的精确程度,另一方面应该分析各参变量的含义,以及估值结果对各变量的敏感性程度。
[1]Gup ta S,Lehmann D,JenniferA.Valuing Customers[J].Journal of Marketing Research,2010,(7).
[2]Aswath D.The Dark Side of Valuation[M].姜万军译.北京:北京大学出版社,2005.
[3]Bauer H H,Hammerschmidt M.Customer 2 based Corporate Valuation[J].Management Decision,2009,(3).
[4]Mittal K,Sinha N,Singh A.An Analysis of Linkage between Economic Value Added and Corporate Social Responsibility[J].Management Decision,2011,(9).
[5]Manfred K,Rudolf M,Sipotz E.Valuation of Customers in Growth Companies2a Scenario Based Model[J].Schmalenbach Business Review,2011,(57).

