数学艇型建模研究

刘明静，李日杰，刘传云

(中国舰船研究设计中心，湖北武汉430064)

0 引言

随着电子计算机技术在船舶设计领域中的应用，用Bezier曲线、B样条曲线来表达船体几何外形的研究已取得很大进展［2］。在Bezier曲线和B样条曲线曲面的基础上又开展了非均匀有理B样条 (nonuniform rational B-spline，NURBS)表达物体几何外形方法的研究［3］。1991年，国际标准组织 (ISO)还把NURBS作为定义工业产品几何外形的唯一数学表达方法。于是，有人就把用Bezier曲线、B样条及NURBS表达的船型称为“数学船型［4］”。严格地说，这种需要用原始型值或中间控制点来进行逼近，并应用计算机进行光顺而得到的船型，并不能算作真正意义上的数学船型。

其原因在于以下3点:一是基于原始型值或中间控制点用样条函数进行表达的船体外形设计，在原理上并没有摆脱传统的由人工干预型值或中间控制点的经验设计本质，设计出的船型性能好坏，在很大程度上仍依赖设计者掌握知识的多寡及设计经验的丰富程度，很难得出优良的船型;二是尽管可以用K×1次NURBS曲面函数来表达船体曲面［5］，但只是粗略地表达船 (艇)体几何形状的离散函数表达式，既不反映船 (艇)型参数，如主尺度、排水量、系数、浮心位置等对船体形状的影响，也不便于自动生成形状各异的多方案船 (艇)型;三是仅是描述船体形状的一个统一的离散表达式，要生成三维船型还需要借助计算机分别对各型线进行拟和、光顺，最终给出型线图和型值表。由此可以看出，基于原始型值或中间控制点的船型并不是真正意义上的“数学船型”，只是一种采用逼近函数而得出的 “数值船型［6］”。

本文针对潜艇开展数学艇型研究，建立艇体三维曲面形状函数［7］，并将SUBOFF的主要参数作为背景参数来拟合SUBOFF艇体曲线［8-9］，以验证本文所建立方法的有效性，从而为今后开展潜艇总体方案自动生成和优化奠定基础。

1 数学潜艇线型表达推导

随着潜艇的发展，现代潜艇的几何外形多呈轴对称的回转体或非轴对称的椭圆形柱体［10］。本文选择轴对称回转体进行推导。

1.1 具有平行中体的流线型回转体的形状特征

回转体潜艇是轴对称几何体，其三维几何形状可用二维图形来表达。二维图形如图1所示。由图中可以看出其艇体的几何形状特征，具体如下:艇体分首进流段、平行中体段和尾去流段3段，段长分别用L1，L2，L3表示，总长为L=L1+L2+L3，直径D=2R。各段的几何形状特征为:首端肥钝，呈长半轴为L1的半个椭球体;平行中体段是半径为R、长度为L2的圆柱体;尾去流段的长度为L3，尾部尖瘦，是剖面素线呈上抛的半抛物线。

图1 带平行中体的回转体潜艇外形示意图Fig.1 The revolution submarine with parallel

1.2 艇体形状的数学描述

根据上述从尾到首由上抛物线、直线和半椭圆曲线构成的二维平面曲线的几何形状特征，分段来构造其数学表达式。图1所示的二维平面曲线是1条半径r(x)沿艇长变化的平面曲线，应用平面椭圆方程、上抛物线函数，这条半径曲线R(x)应满足表1和表2的条件。

表1 半径曲线的几何性状Tab.1 The geometrical properties of radius function r(x)

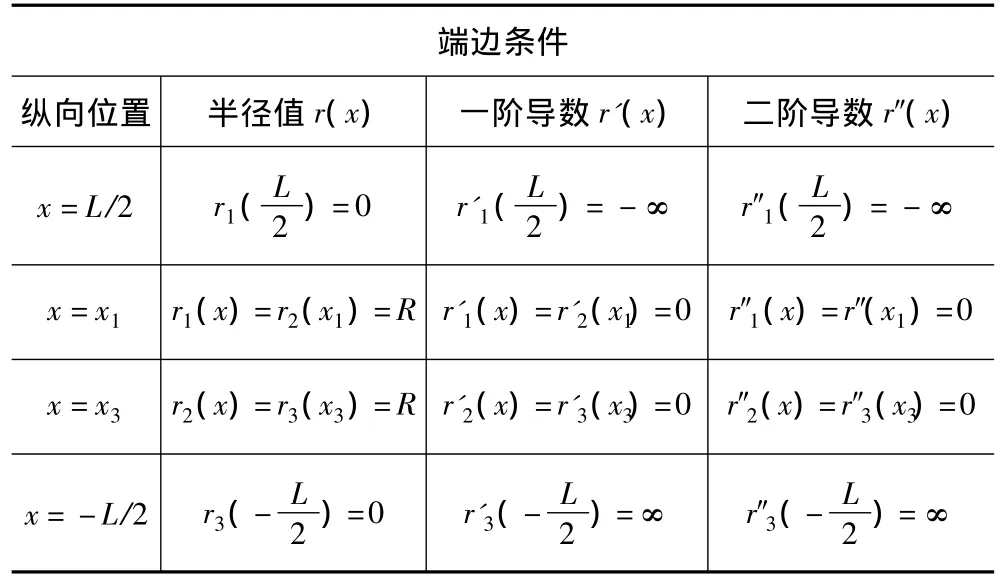
表2 半径曲线的端边条件Tab.2 Boundary condition of radius function r(x)

根据表1和表2，获得的轴对称回转体半径函数统一表示为:

其中:α1与α3为参变量，表征了首、尾段的丰满程度，与艇体排水量▽及浮心纵向坐标xc密切相关，也可以说参变量α1和α3与主尺度L，D，菱形系数Cp，中横剖面系数CM以及浮心纵向坐标位置xc密切相关。由于排水体积▽ =CpCMLBT(=CpCMLD2)(D=2R为艇的直径)。不同的▽和xc将对应不同的α1与α3;对给定的▽和xc来说，参变量α1和α3将是1对固定值。

系统进行底层模块的注册时，智能节点首先广播下发问询数据包，各底层模块接收后根据ID号延时反馈注册数据包，智能节点上发底层模块注册信息至监控终端，等待用户确认底层模块是否属于该节点，用户在监控终端输入底层模块涂层的验证密码进行确认。智能节点的Flash开辟了两块区域，对底层模块的ID信息进行存储，用户确认的底层模块属于该智能节点，云服务器下发确认信息至智能节点，底层模块ID信息存入Flash第一区域，用户未确认的底层模块不属于该节点，云服务器下发未确认信息，模块ID信息存入Flash第二区域，智能节点接收到不属于该节点的底层模块反馈的数据时滤除不再上发至云服务器，无线自组织网络建立完成。

1.3 形状函数表达式

应用圆方程，得到艇的形状函数为:

1.4 形状参数的确定

式(2)中有2个表达半径曲线和艇体形状变化的未知因子nf与nα需要确定。这需要补充艇的水下排水量D和水下纵倾均衡条件xG=xc这2个条件方程来确定。因只涉及到坐标变量x=Lξ，故用式(2)来构建条件方程。

排水量约束条件:

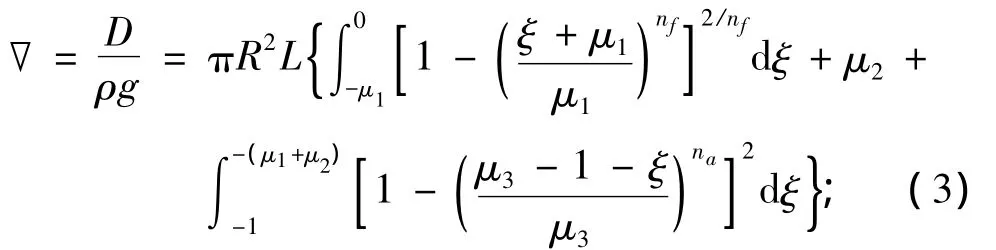
浮心纵坐标约束条件:

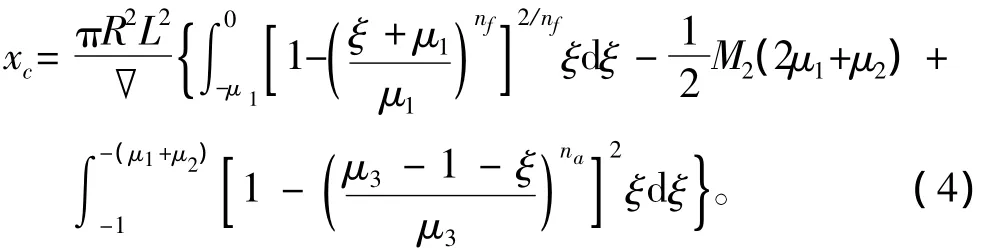
上述2式为1个方程组，在所有的参数都给定的情况下，2个方程有2个未知数α1与α3，方程组有唯一解;当解开1个约束参数，如xc，则方程组为不定方程，具有无数解，方程组解的含义为满足排水量和3段长度要求下的“小小系列”;当解开2个约束条件，如xc与▽，则方程组所形成的循环称为“小系列”;当解开更多的约束条件，以此类推可形成“中系列”甚至“大系列”等。为便于阐述整个优化原理，本文中后面的算例以变化xc为例，进行阐述。

2 算例

为对回转体“数学艇型”进行实用性检验，本文选取SUBOFF-8潜艇模型作为比较对象。SUBOFF艇型是美国经过长期试验研究而得出的优良回转体艇型系列，其试验结果被许多国家用来作为检验现代潜艇线型优劣的标准。

为便于与SUBOFF艇型对比，本数学艇型计算实例选取与SUBOFF-8艇体模型相同的主尺度、排水量与浮心纵向坐标位置。SUBOFF-8模型参数示于表3。

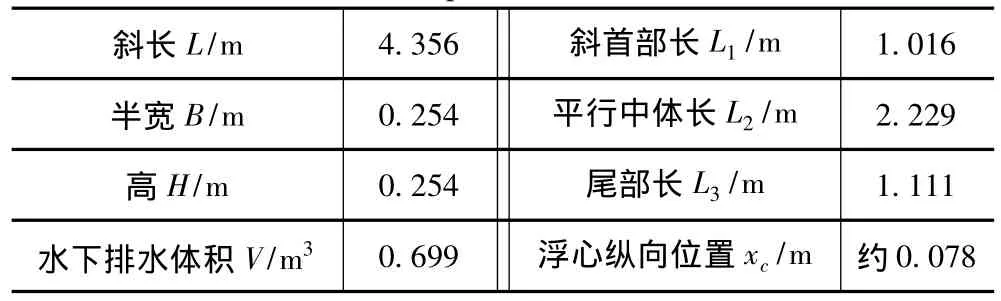
表3 SUBOFF-8主要参数表Tab.3 The main parameters of SUBOFF-8

实例演算过程如下:

1)应用表3中的参数，代入排水量和浮心纵向坐标位置约束条件方程组，解出未知参数α1与 α3。

2)将解出的α1与α3代入回转艇体形状函数式(2)，便得到满足SUBOFF-8艇参数要求的函数表达式如下:

将表3中▽ =0.699，L=4.356，R=0.254，xc=0.078代入式(5)后，可解出2个未知参变量，得α1=0.439 5，α3=1.415 6。代入半径函数公式，得SUBOFF的半径函数为:

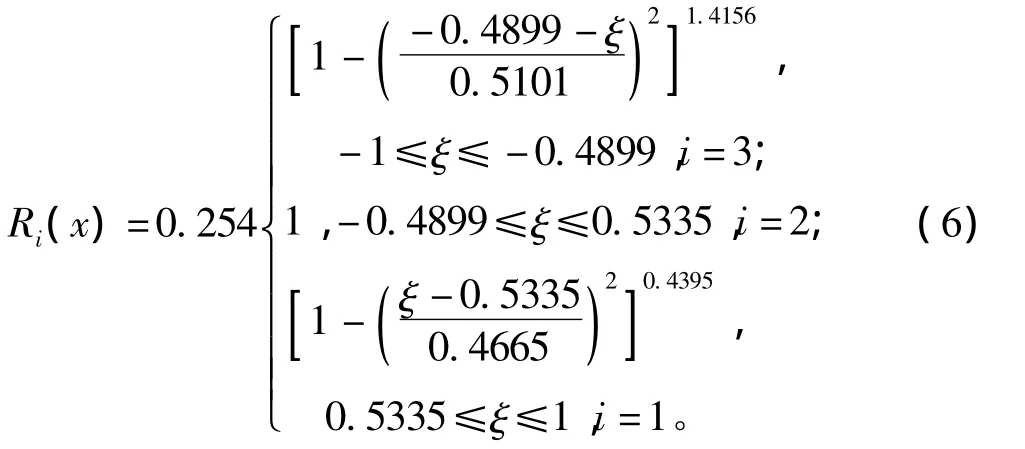
图2 由数学潜艇模型得出的SUBOFF近似艇Fig.2 The Comparison of calculated and SUBOFF form

由于参考浮心纵向位置xc精度不高，式(6)计算结果所得的剖面形状函数见图2。图中实线为根据本文方法计算的剖面线，虚线为根据文献发布的SUBOFF型值而绘制的剖面线。从图中可见，二者图形大部分重合，计算误差很小。在浮心纵向位置精度足够的情况下，二者的线型可完全重合。这一结果表明本数学潜艇模型完全能够准确地描述SUBOFF潜艇的外形形状。根据式(6)，求得的SUBOFF艇的形状函数为:

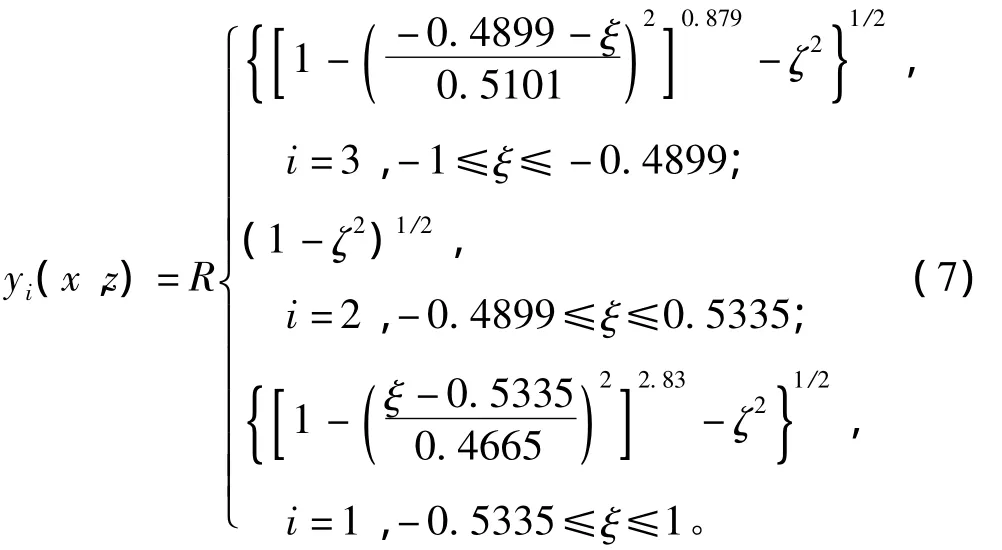
3)系列艇型。解除浮心纵向位置坐标的约束，则形成的艇型约束方程为

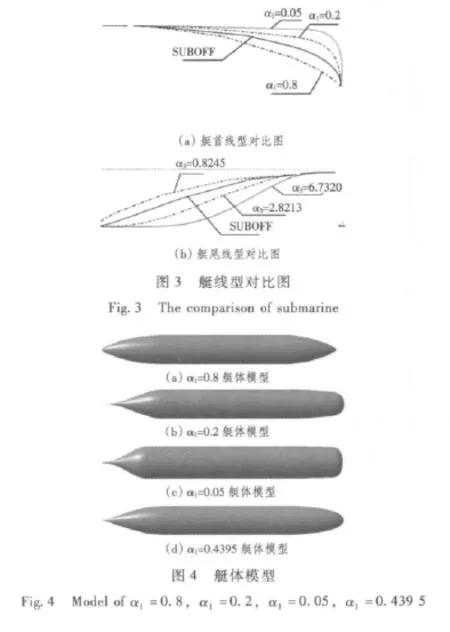
在其他参数都约束的情况下，式(8)为不定方程，具有无数解，即“小小系列”艇型。在α1取值范围内任取几个值，则可得出相应的艇型，如图3所示。

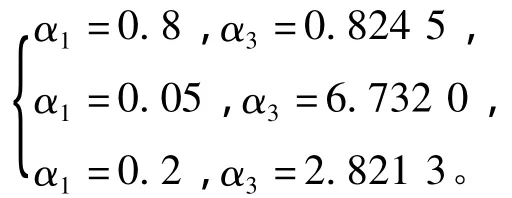
上述各艇型对应的三维图形如图4所示。从图中可见，本文采用的方法可表示形状各异的艇体外形。艇体首部为减函数，即α1越小，首部越丰满。

3 结语

本文建立的数学艇型三维艇体函数，将设计参数和形状参数联系起来，构建了满足设计要求的艇体模型自动生成体系。通过在体系中改变约束参数个数 (本文中仅改变浮心纵向位置)，可以得到不同等级的系列艇型，如“小小系列”、 “小系列”等，从而为总体方案的自动生成奠定基础。该方法建立了艇型设计与总体方案设计的联系［11］，大大减少了艇型设计中的循环次数，可获得具有实用价值的艇型，对潜艇总体设计具有很大的指导作用。

［1］杜月中，闵建，郭字洲.流线型回转体外形设计综述与型线拟合［J］.声学技术，2004，6(23):93-100.DU Yue-zhong，MIN Jian，GUO Zhi-zhou.A review and mathematical formation of shape design of streamlined bodies of revolution［J］.Technical Acoustic，2004，6(23):93-100.

［2］刘可峰.船舶型线建模系统研究［D］.哈尔滨:哈尔滨工程大学，2005.2.

［3］黄绪琼.潜艇主艇体过渡型型线的数学设计方法［J］.舰船科学技术，1998(1):1-6.HUANG Xu-qiong.The mathematical hulllines for submarine main body［J］.Ship Science and Technology，1998(1):1-6.

［4］陈绍平.NURBS曲线及其在船舶型线设计中的应用研究［D］.武汉:武汉理工大学，2002.

［5］林小平.潜艇水动力计算及型线生成研究［D］.武汉:武汉理工大学，2005.

［6］沈泓萃，韩瑞德，许鸿生.流线型回转体的数学表达和几何特征［J］.舰船性能研究，1976(2):60-83.SHEN Hong-cui，HAN Run-de，XU Hong-Sheng.The methmatical description of streamlined revolution［J］.Ship performance research，1976(2):60-83.

［7］KARLSSON A，FUREBY C.LES of the Flow Past a 6∶1 Prolate Spheroid［C］.47thAIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition.Orlando，Florida.2009.

［8］JEANS T L.High-resoltion reynolds-averaged navier-stokes flow predictions over axisymmetric bodies with tapered tails［J］.AIAA Journal，2009(1):19-23.

［9］CINDY C W.Steady and unsteady force and moment data on a DARPA2 submarine［D］.1999.

［10］FUDGE D M，ZINGG D W.A CAD-free and a CAD-based geometry control system for aerodynamic shape optimization［C］.43rdAIAA Aerospace Science Meeting and Exhibit，Reno，Nevada，2005.