基于PSCAD的大型机组失步保护仿真与整定校验
王玉龙,王宝华,陆桂华,杨支吉
(1.南京理工大学 自动化学院,江苏 南京 210094;2.江苏省仪征供电公司,江苏 仪征 211400)
0 引言
近年来,电网及机组的容量不断增大,使得失步振荡时振荡中心常落在发变组内,其中振荡电流很大,会引起发电机定子过热过流而损害发电机。另外失步振荡可能破坏系统的稳定性,波动中的电压、电流会对用户的用电和负荷的供电产生影响,可能会扩大事故范围[1-3]。同时,规程中规定300 MW及以上发电机组需配置失步保护[4]。因而,对失步振荡机理深入研究,并分析失步判据来完善大型发电机组失步保护的配置受到越来越多的关注。
电厂在配置和整定发电机的失步保护时,现有的三元件型和双遮挡器判据都可以区分失步振荡中心在发变组内部还是外部,可以整定失步保护跳闸允许电流,整定区内和区外不同的滑极次数,区分失步故障与其他故障[4-5],但要加强失步预测[6]。从这个角度讲,将失步预测运用到现有的失步判据中,能更好地配置大型发电机组的失步保护。
本文采用PSCAD/EMTDC电磁暂态仿真软件建立了某发电厂的仿真系统模型。根据失步故障特点建立三元件型与基于等面积原则的失步预测相结合的失步保护模型,验证保护在各故障下发信及动作的情况,为具有多台机组的电厂失步保护动作的滑极次数确定及出口动作方式确定提供依据。
1 失步判据原理及整定
1.1 三元件型失步判据[7-11]
依据失步时的阻抗轨迹变化规律,保护采用由1个透镜型阻抗元件和2个直线阻抗元件构成的三元件型失步判据模型,如图1所示。
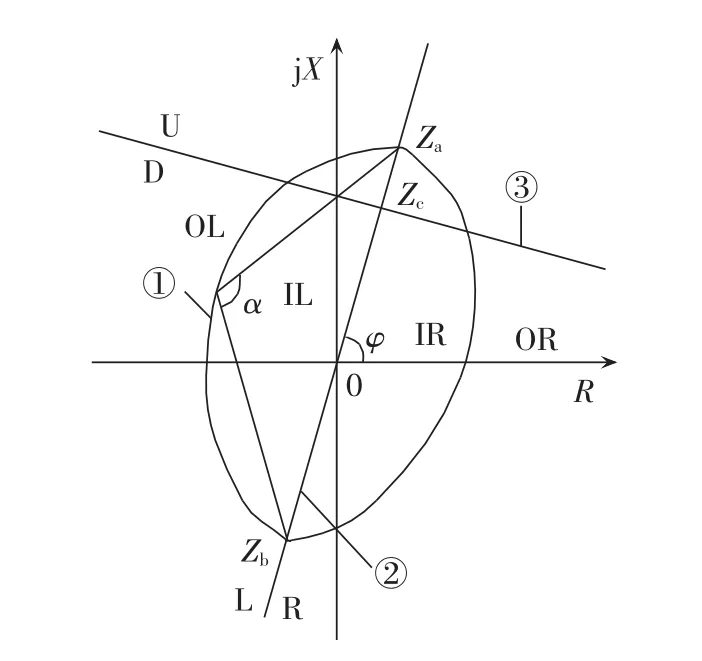
图1 三元件型失步判据动作特性Fig.1 Operating characteristics of three-component criterion for out-of-step protection
根据图1,失步振荡后,若机端测量阻抗轨迹依次穿过OR-IR-IL-OL或OL-IL-IR-OR,且在透镜中满足一定时间,分别判为加速与减速失步。轨迹穿越透镜时在电抗线③下面即经过D区,说明振荡中心位于发变组内部,判断此时失步为区内失步;反之,轨迹穿越透镜时经过U区,说明振荡中心位于发变组以外的系统,判断为区外失步。
1.2 基于等面积原则的失步预测
失步预测模型就是将等面积原则下的Pe-δ曲线转化到 Pe-t曲线[12-13],即将图 2转化到图 3。
图2、3中δ0为故障前功角;δc为故障切除时功角;δmax为振荡时最大功角;t0为故障发生时刻;t1为机械输出功率Pe超过机械输入功率PT线的时刻;tmax是稳定振荡时δ=δmax的时刻或不稳定振荡时δ=π-δ0的时刻。
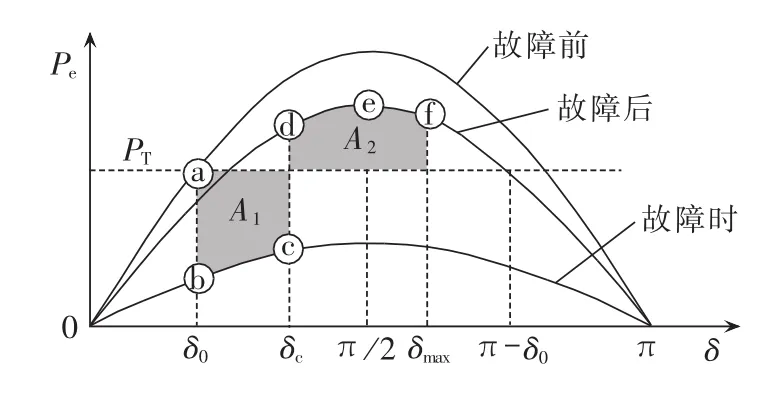
图2 Pe-δ曲线Fig.2 Pe-δ curve
由加速面积A1和减速面积A2的和来判断,式(1)和(2)的数学积分模型实现等面积原则的失步预测。
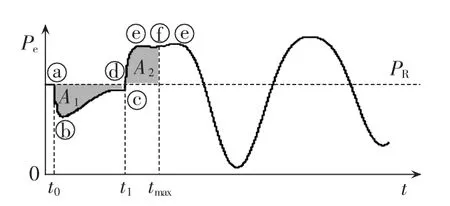
图3 Pe-t曲线Fig.3 Pe-t curve
稳定振荡:
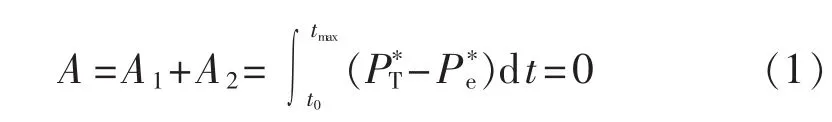
失步故障:
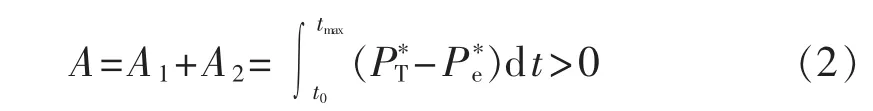
其中,PT*、P*e分别为机械输入功率标幺值和输出功率标幺值。
根据等面积原则,故障切除后如果系统稳定则找到在振荡的第1周期内的最大振荡功角的时刻,从而根据式(1)求出面积和A;如果为不稳定振荡,则直接找到π-δ0的时刻,由式(2)积分后发信号。
1.3 保护整定计算
根据图1中的动作特性,遮挡器特性第一象限阻抗为Za、第三象限阻抗为Zb、阻抗角为φ。对图4所示系统进行整定计算。
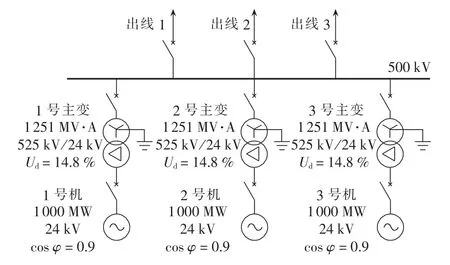
图4 电厂电气主接线图Fig.4 Main connection diagram of power plant
3台机组参数相同,则整定结果(计算和仿真都取一次值,不考虑互感器变比)也相同,发电机额定容量Sgn为1111 MV·A,额定电压 Ugn为 24 kV,发电机的暂态电抗 X′d=0.382 p.u.,次暂态电抗 X″d=0.269 p.u.,变压器的短路阻抗 XT=0.1314 p.u.,最大、最小运行方式系统等值阻抗分别为Xs.min=0.070 7 p.u.、Xs.max=0.3020 p.u.,发电厂中发电机的台数n=3,基准阻抗Zgn为:
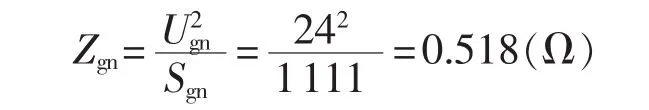
Za、Zb和电抗特性Zc的整定公式分别为:
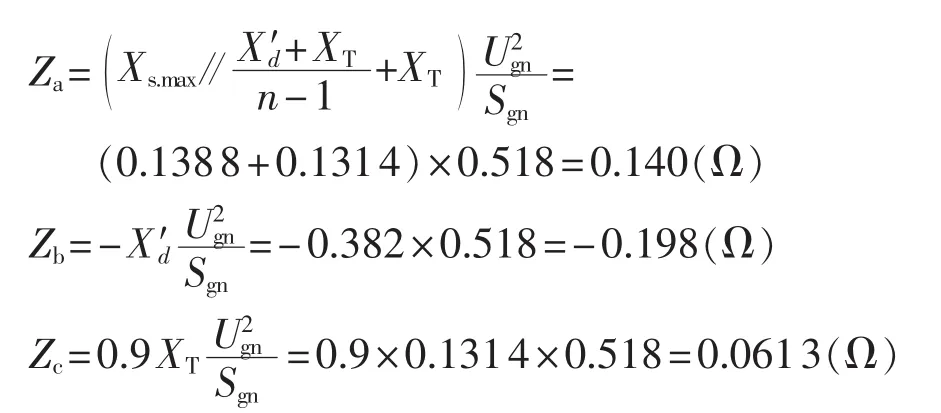
灵敏角 φsen推荐取 80°~85°,这里整定为 80°。
透镜内角α的整定:根据工程经验,建议整定为120°。
发电机的滑极次数整定:振荡中心在区外时,失步保护动作于信号,滑极次数可整定为2~15次;失步保护动作于跳闸,滑极次数整定为大于等于15次;振荡中心在发变组内时,1号、2号、3号机组滑极次数分别整定为2、4、6次,动作于跳闸。
出口方式的整定:单机运行时,最小、最大运行方式下系统的振荡中心分别为:
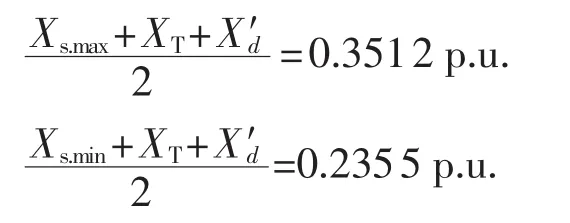
故振荡中心在发变组内,保护动作于停机。
2 失步仿真建模
本文根据某电厂单机容量为1000 MW的3台汽轮机的主接线图4及各元件参数,在PSCAD软件中建立了与电厂实际参数一致的仿真模型,发电机带有自励磁系统、稳定器和调速器。在PSCAD软件中建立的三元件型失步判据仿真模型和等面积预测失步的仿真模型分别如图5、6所示。
图5中,透镜元件由两同半径的圆的相交部分构成。模块a实现测量轨迹在透镜中的延时,模块b判断轨迹是否穿过挡板及透镜,模块c为轨迹与电抗线比较模块,用来判断区内失步。当模块a、b、c三部分同时满足,通过逻辑与门就给由D触发器构成的异步计数器(模块e)1个计数脉冲实现1次滑极计数,最终实现了三元件型的区内失步判断。当滑极次数计满后通过断路器实现出口动作。区外判断由图中的模块 a、b、d 实现。
经过整定计算得到2个圆的半径是0.195ω,圆心分别为(0.091,-0.0456)、(-0.1011,-0.0118)。
图6中,模块1用于寻找在第1振荡周期中功角到达π-δ0的时刻,而模块2用于故障切除后通过差分法寻找稳定极限角的时刻。根据模块1、2振荡的类型选择模块3中积分的上限时刻:失步振荡时积分上限为模块1得到的时刻π-δ0,反之为模块2得到的时刻。最终,将输入功率PT与输出功率Pe比较,并积分求出面积实现失步的预测。

图5 三元件型失步判据模型Fig.5 Model of three-component criterion for out-of-step protection
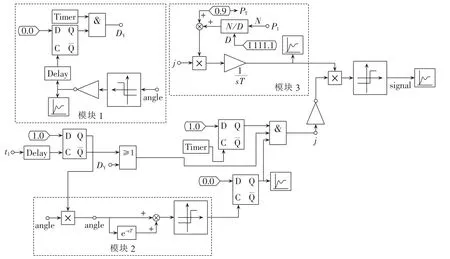
图6 等面积的失步预测模型Fig.6 Out-of-step prediction model based on equal area criterion
3 失步保护仿真结果
3.1 失步故障时各机组失步保护动作情况
变压器高压侧三相短路,故障0.5 s后切除,3台机组都失步。1号机机端测量阻抗轨迹如图7(a)所示,轨迹在透镜中穿越2次,然后发电机被三元件型失步判据切除,穿越脉冲和三元件动作行为见图7(b)。图 7(b)中,积分后的面积(标幺值,后同)大于0,等面积原则的预测失步信号在第1条虚线所示时刻发出,早于三元件型判据动作时刻(第2条虚线所示时刻),有很好的预测性,便于工作人员给发电机采取必要的措施如增减有功、切除部分机组、调相、投电气制动等。
而2号和3号机组的测量阻抗轨迹分别穿越透镜4、6次后也相继被切除。可见发电厂需要给每台发电机配置失步保护,采取不同的滑极次数来实现不同的延时切机,且增加了失步预测可以给电厂争取机组再同步的时间。
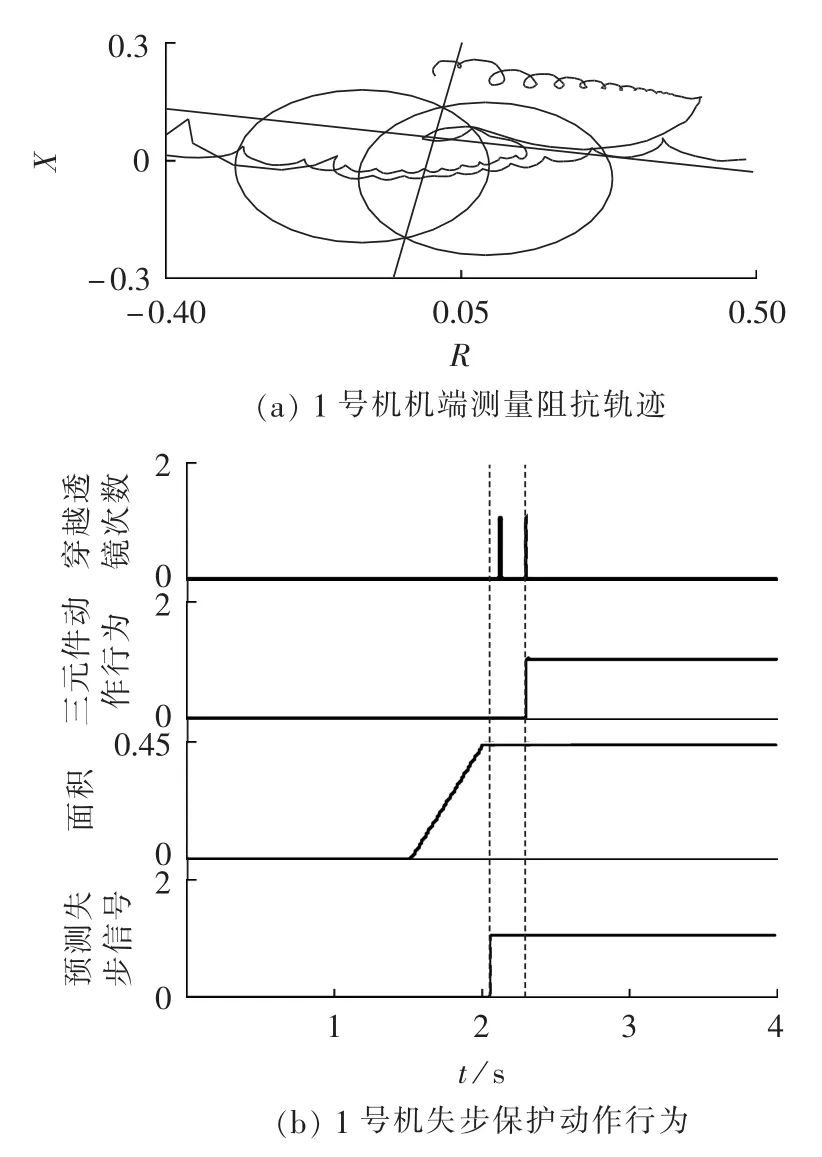
图7 失步振荡时阻抗轨迹和失步保护动作情况Fig.7 Impedance path and operation of out-of-step protection during out-of-step oscillation
3.2 稳定振荡时各机组失步保护的动作行为
同样在变压器高压侧三相短路故障,0.1 s后切除,系统发生稳定振荡。
稳定振荡时,各机组机端测得的阻抗轨迹一致,阻抗轨迹基本在第一象限振荡,不会穿越透镜,如图8(a)所示。图 8(b)中,失步预测模型积分后的面积为0,失步保护不发失步预测信号也不动作,保证了失步保护具有鉴别稳定振荡和失步振荡的能力。
3.3 1号机失磁故障时机组失步保护动作行为
仿真时1号机在1.5 s失磁故障,并为1号机加入了由异步圆阻抗、逆无功和转子低电压判据构成的失磁保护[14-16]。失磁故障中阻抗轨迹如图9所示,失磁保护由阻抗判据延时0.8 s切机,动作时刻为图10中虚线所示时刻。失步保护能准确发失步预测信号(点划线所示时刻)但不动作,如图10所示。
如果失磁保护拒动,失步保护作为失磁保护的后备保护能可靠动作。仿真结果如图11所示,轨迹在透镜中穿越2次后(虚线所示时刻)失步保护动作。
3.4 短路故障时机组失步保护动作行为
在变压器高压侧发生短路故障,如不切除最终会引起发电机失步,失步保护应作为后备可靠动作,以两相短路为例研究其动作行为,仿真时在1.5 s发生短路故障且不切除。失步保护的动作行为见图12,一旦反应短路故障的保护拒动,失步保护准确在点划线所示时刻处发失步信号,并在故障持续1 s后可投入做其后备而动作,动作时刻为虚线所示时刻。
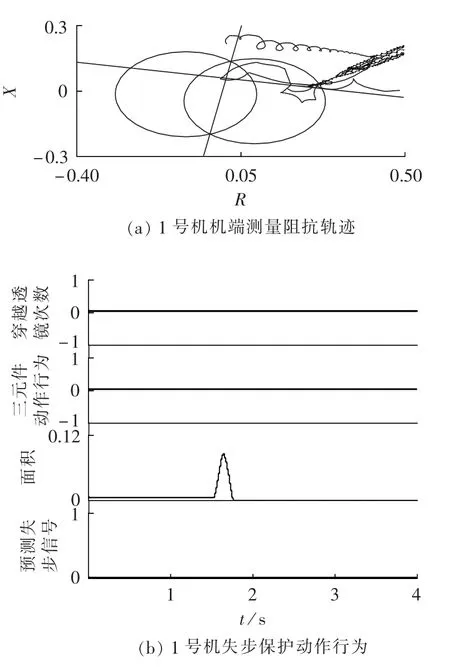
图8 稳定振荡时阻抗轨迹和失步保护动作情况Fig.8 Impedance path and operation of out-of-step protection during stable oscillation
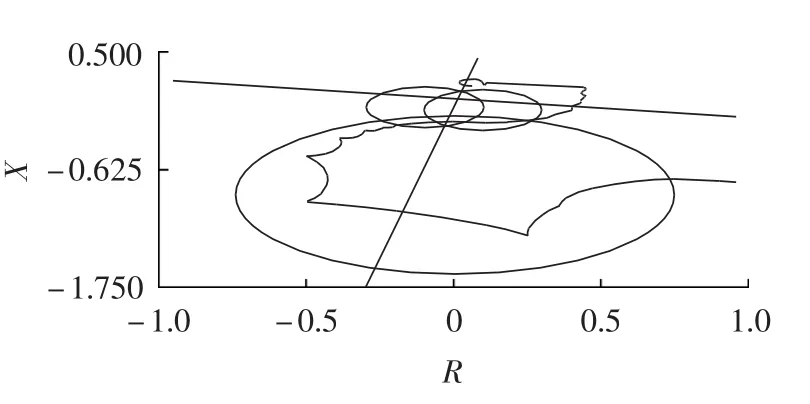
图9 失磁故障时测量阻抗轨迹Fig.9 Measured impedance path during loss-of-excitation fault
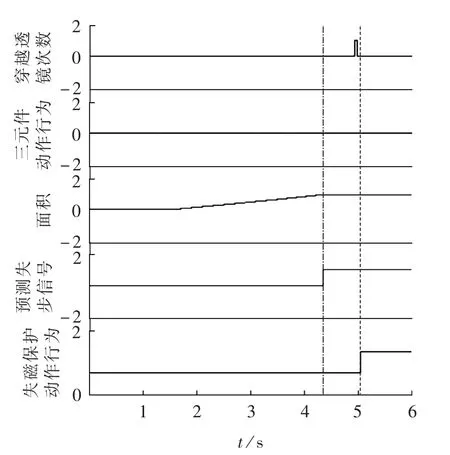
图10 失步保护和失磁保护动作情况Fig.10 Operation of out-of-step protection and loss-of-excitation protections
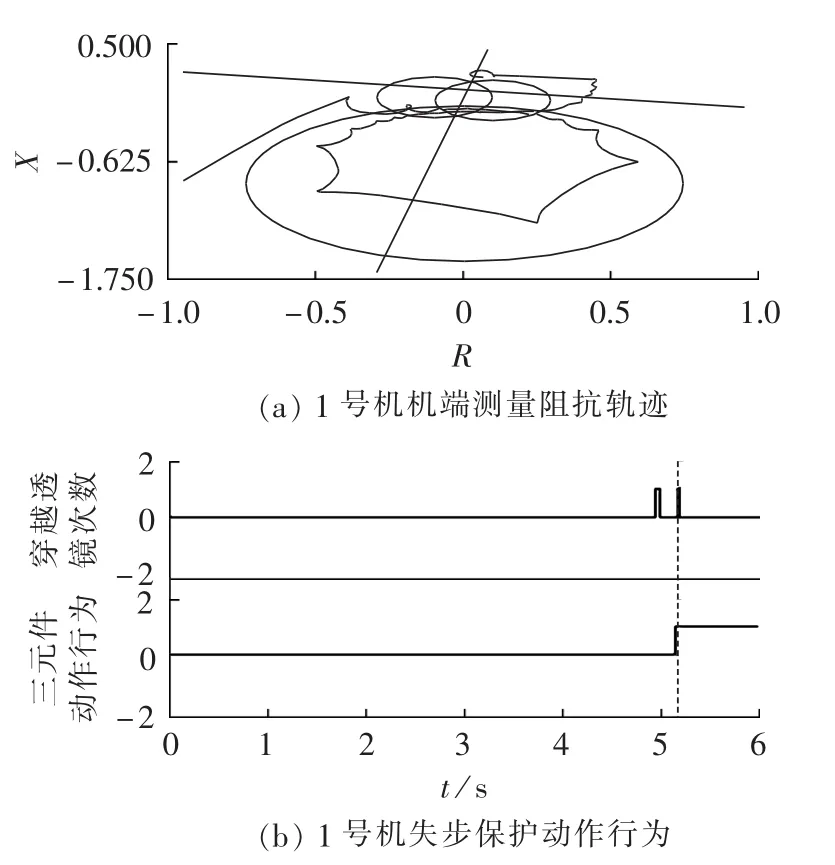
图11 失磁保护拒动时阻抗轨迹和失步保护的动作行为Fig.11 Impedance path and operation of out-of-step protection with loss-of-excitation protection misoperation
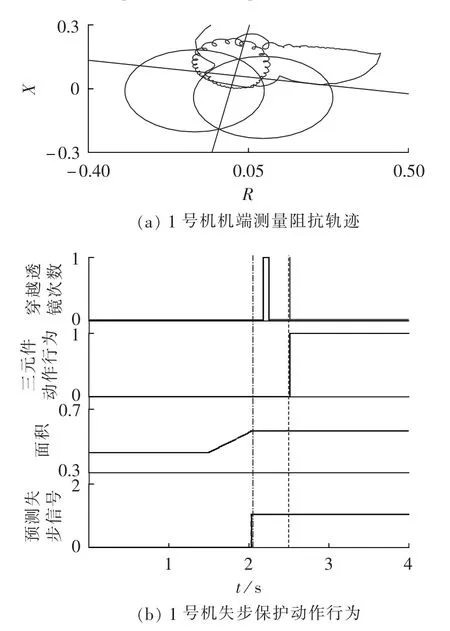
图12 短路故障时阻抗轨迹和失步保护的动作行为Fig.12 Impedance path and operation of out-of-step protection with short circuit
4 结论
本文在PSCAD软件中建立了某电厂的三机无穷大系统仿真模型,能够真实地模拟该电厂的各种运行情况。在完成了该电厂三机组的失步保护的整定计算后,针对现有失步保护中需增设失步预测功能,提出了等面积原则的失步预测,能为即将失步的机组争取再同步的时间。同时,在PSCAD软件中建立的此失步预测与三元件型判据相结合的失步保护仿真模型,仿真结果验证了失步保护整定的正确性,而且能精确地预测不稳定振荡并发出失步信号,且能在各种故障下不误动,通过滑极次数切除由各种故障引起的失步故障,可以用于大型发电机组的失步保护的配置与整定方面的研究。

