考虑可靠性约束的含风电场电力系统动态经济调度
姜 文,程叶霞,严 正,冯冬涵
(上海交通大学 电气工程系,上海 200240)
0 引言
随着能源以及环境问题的日益突出,可再生能源尤其是风电在世界各国得到了广泛的应用,引起了足够的重视。美国能源部计划到2030年风电将供应全美20%的负荷[1];欧盟能源委员会也提出20/20/20目标,即到2030年温室气体排放量减少20%、新能源占总能源比重的20%、能源消耗减少20%[2];2010年底,中国风电累计装机容量达到40 GW,跃居世界第一。预计到2015年,中国风电总装机容量将达到90~150GW。然而风电具有随机性和间歇性,大量风电的并网将给电网的运行带来巨大的挑战[3]。
传统的电力系统经济调度分为静态经济调度和动态经济调度[4-8]。静态经济调度是对电力系统的某个时间断面求取目标最优,只考虑静态约束,没有考虑不同时间断面之间的内在联系;而动态经济调度考虑了不同时间断面的耦合性,如发电机爬坡率等,因此计算过程比静态经济调度复杂,但计算结果更符合实际要求。风电的随机性和间歇性,以及风电并网容量的逐渐增加,使含风电场的电力系统动态经济调度的研究变得越来越重要。目前,国内外学者对于含风电场的电力系统经济调度做了一些初步研究,并取得了一系列成果。文献[9-11]引入了正、负旋转备用约束,以应对风电功率预测误差给系统调度带来的影响,此方法是按照风电出力的百分比增加系统的旋转备用;文献[12]采用随机规划理论中的机会约束规划模型用来描述风电随机性及其带来的影响;文献[13]在研究含风电场的电力系统动态经济调度模型时,将可利用的风电功率作为服从Weibull分布的随机变量,在目标函数中加入了过、欠风电预测时相应的备用和惩罚项,用以模拟风电随机性对系统的影响;文献[14]通过限制风电场并网容量,从而降低风电随机性对系统的影响,这种方法降低了风电场的利用率,造成了资源的浪费;文献[15]利用模糊理论建立含风电场的电力系统动态经济调度模型,可以得到既满足一定风险、又实现一定经济效益的调度方案,但隶属度函数引入了一定的人为因素;文献[16]研究了同时含风电和太阳能发电的机组发电问题,采用模糊最优化方法应对新能源随机性对系统带来的影响。然而以上研究,都是按照百分比设置备用的方法来应对系统的不确定性。这些方法不是过多地设置备用,造成浪费、不经济,就是备用过少,满足不了系统可靠性的要求。随着风电并网的增加,系统的不确定性进一步加剧。因此,为了满足用户供电可靠性的要求,在研究电力系统动态经济调度策略的时候,有必要考虑系统可靠性约束。
本文提出了一种考虑系统可靠性约束的含风电场电力系统动态经济调度模型,该模型除了考虑机组常规的运行约束外,还加入了可靠性约束,在目标函数中计及了中断负荷费用,使得该优化调度模型更符合实际运行的需要。以IEEE-RTS测试系统为算例,仿真分析了各种情况对系统运行费用的影响,验证了模型的可行性和有效性。
1 风电、负荷预测的不确定性
1.1 负荷预测
短期负荷预测方法很多,而且应用也比较成熟。本文假设负荷序列已经通过某种预测方法获得。由于负荷预测总会存在误差,本文采用高斯分布来模拟预测误差,并假设预测误差均值为零、标准方差正比于负荷[17-19]。

其中,dtF为时间t的预测负荷,dtA为时间t的实际负荷,etd为负荷预测误差。
根据文献[17],负荷预测误差的标准方差用实际负荷的百分比表示:

其中,c是常数,通常取 1~3。
1.2 风电预测
风电预测是风电研究领域一个非常重要的问题,目前已经有多种预测方法,然而预测误差依然很大。本文采用自回归滑动平均ARMA(Auto Regres-sive Moving Average)模型结合广义自回归条件方差GARCH(Generalized AutoRegressive Conditional He-teroscedasticity)模型预测风速,并采用处理负荷预测的方法,认为风电预测值为风电实际值加预测误差。

通常情况下,风电预测误差要大于负荷预测误差,而且预测误差会随着预测时间增加而增加。本文采用文献[19]中的方法,认为预测误差符合均值为零的高斯分布,并假设在24 h内,风电预测误差的标准方差近似为:

其中,sw表示风电方差随机变量,一般取5;Wc是风电场总的安装容量。
1.3 净负荷
本文将风电看成是负的负荷,引入净负荷的概念。净负荷用负荷预测值与风电预测值之差来表示。

从上式可知:净负荷预测值可表示为净负荷实际值加上净负荷预测误差。由于风电预测误差和负荷预测误差的非相关性,净负荷预测误差的标准方差可表示为:

对于净负荷,本文采用七分段的高斯分布来模拟预测误差的不确定性。
2 数学模型
2.1 目标函数
电力系统动态经济调度的目标是在满足负荷和运行约束的前提下,合理地分配电网中各发电机组的出力使得调度期间发电总成本最小。本文利用中断负荷的费用来反映可靠性成本因素。由于风力发电不需要消耗日益减少的燃料,因此假设电力公司首先调度风电。在不考虑风电场运行费用的情况下,优化目标的表达式为:

其中,F为调度运行的总费用;T为调度运行时间;N为发电机台数;Pi,t为发电机i在t时段的出力;E为系统中断负荷期望;V为单位MW·h中断负荷的费用;Fi,t(Pi,t)为发电机 i在出力为 Pi,t时的费用;ai、bi、ci为机组i燃料费用系数。
2.2 约束条件
a.功率平衡约束。

其中,PWTt、PLDt为 t时段风电场出力以及系统负荷值;PLCt为t时段系统切负荷值。为方便计算,模型中忽略了系统损耗。
b.运行约束。

其中,Pimax、Pimin是发电机 i的出力上、下限。
c.旋转备用约束。
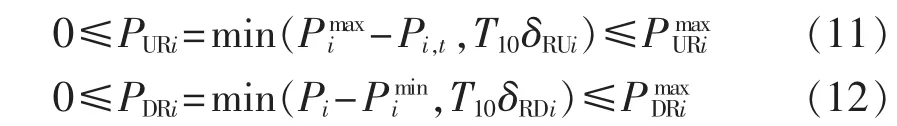
其中,PURi、PDRi分别为机组i所提供的正、负旋转备用;T10为旋转备用响应时间,为 10 min;δRUi、δRDi分别为机组i的上、下爬坡率;
d.发电机爬坡率约束。

其中,T60表示一个运行时段1 h,即60 min。
d.线路传送容量约束。

其中,flmax表示线路l传输容量上限,Ll表示线路l的传输潮流。对于此约束,本文先进行经济调度计算,再利用直流潮流进行校验。
e.系统可靠性约束。

其中,Emax为系统切负荷上限。
3 改进的粒子群优化算法
粒子群优化(PSO)算法已经广泛应用于各种优化问题[20-22]。为求解考虑可靠性约束的含风电场电力系统动态经济调度问题,本文提出了改进的粒子群优化(IPSO)算法,该算法引入信息分享和精英学习策略。
3.1 信息分享策略
在信息分享策略中,使用式(17)来更新粒子的速度[20]:

其中,ω表示惯性系数;pkbesti,t表示粒子i搜索到的最优值;gkbesti,t表示全局最优值;pkbestr,t表示从 所有粒子最优值中随机选出的3个中最大的一个值;xki,t表示粒子i当前位置;c1和c2表示群体认知系数;Psi表示信息分享率。在粒子速度更新之前,首先产生一个随机数,如果此随机数大于等于Psi,则粒子速度的更新将趋向于全局最优值,否则利用pbestr,t代替全局最优值。本文信息分享率被定义为:

其中,N表示所求问题的维数;r表示当前的仿真次数;rmax表示最大仿真次数。
pbestr,t按下列原则产生:
a.从所有的粒子中随机地选择3个;
b.比较它们的适应值,选最好的一个为pbestr,t;
c.pbestr,t将会分享它的所有信息(各个维数)。
3.2 精英学习策略
和其他的粒子不同,全局最优粒子没有更好的粒子为目标,因此需要新的动力来推动它朝向潜在的最优解靠近。如果找到一个比全局最优粒子较优的解,则用此解代替全局最优解,然后其余的粒子跳出局部最优,往新的全局最优解收敛[21]。
在精英学习策略中,设置参数a为全局最优解连续没有被更新的次数,aN是参数a的阈值。当参数a值增加到aN时,精英学习策略开始起作用。本文精英学习策略中,选取全局最优解的一维Pd(根据机组出力费用灵敏度大小选取)作为扰动项。之所以仅选择一维,是考虑到局部最优很有可能具有全局最优的部分结构,因此这部分应该给予保护。精英学习策略通过Bata分布表示如下:

搜索范围[Xdmin,Xdmax]是所求问题的上、下限值。Betarnd(α,β)是一个参数为α和β的随机 Bata分布。在Bata分布中,均值μ=α/(α+β),方差 σ=,本文选β为1。类似于一些时变的神经网络训练策略,设α随着仿真次数线性变化:

其中,αinitial、αfinal分别是α的初始值和终值,根据经验取αinitial=1.0、αfinal=0.2,精英学习策略流程图见图1。
4 算法流程
IPSO算法将信息互享策略和精英学习策略相结合,进而增强了搜索能力以及跳出局部最优的能力。所提算法求解考虑可靠性约束的含风电场电力系统动态经济调度的流程如下。

图1 精英学习策略流程图Fig.1 Flowchart of elite learning strategy
步骤1 输入系统参数。
输入机组参数、负荷预测序列值以及风速序列,根据预测风速计算各个时段风电场的出力;利用七分段的高斯分布模拟净负荷预测误差的不确定性,求解各种情况的概率。
步骤2 初始化IPSO参数。
设置参数:粒子总数J=30,最大仿真次数rmax=1000。本文使用动态惯性系数如下:

其中,r表示仿真次数;ωinitial、ωfinal分别为惯性系数的初始值和终值,分别设置为0.9和0.4。
使用时变的加速度系数如下:

其中,c1f、c1i和 c2f、c2i分别是 c1、c2的终值和初始值。从经验值来看,当c1从2.5到0.5变化、c2从0.5到2.5变化时,可以得到最优值;aN取4。
步骤3 产生初始值。
随机产生粒子初始值 xkj(j=1,2,3,…,J),每个粒子xjk包含发电机的有功出力,是一个N×T的矩阵,其中每个元素 Pi,t(i=1,2,…,N;t=1,2,…,T)在整个可行域内均匀分布。
步骤4 评估每个粒子的适应值。
适应值是评估每个粒子优劣的标准,式(24)描述了考虑可靠性约束的动态经济调度函数适应值:

其中,βm是约束惩罚因子,Qkj,m,t是惩罚函数。
步骤5 更新粒子速度与位置。
产生一个随机数 R,然后根据式(7)、(8)更新粒子的速度,再根据式(33)更新粒子的位置。

步骤6 精英学习策略。
判断a是否等于aN,如果是,则采用精英学习策略使最优粒子跳出局部最优。
步骤7 结束判断。
如果满足结束条件,程序停止,否则由式(21)—(23)更新惯性系数和加速度系数,然后循环步骤4至步骤6,直至程序结束。
步骤8 使用直流潮流计算系统线路潮流是否越限,如果不越限,则为系统最优值。
5 算例分析
5.1 仿真数据
为验证所提算法的有效性,本文采用IEEE-RTS测试系统,系统负荷采用24时段,负荷数据来自文献[23],机组参数可以通过文献[24]获得,系统中保留26台机组,去除6台水电机组。风电场是由100台双馈异步风机V90-2MW组成,风速数据来至东海风电场。在系统运行时段,风电场预测出力如图2所示。

图2 预测的风电场出力Fig.2 Forecasted wind power output
本文机组采用两状态模型,假设系统的前导时间较短,以至于故障机组在前导时间内来不及维修和更换[25]。在这种情况下,机组的停运概率可以用停运替代率 ORR(Outage Replacement Rate)表示,即:

其中,TL表示前导时间,λi表示机组的故障率。利用停运容量概率表求解系统可靠性指标E,累积概率截止到 10-13。
系统参数如下:前导时间TL=4 h,风电机组安装容量Wc=200MW,负荷随机参数c=1,V=1000,sw=5,中断负荷上限Emax取系统负荷的1%;IPSO参数取值同第4节。
由于IPSO算法是一种随机寻优方法,为保证计算的精度,本文每种参数情况下都运行50次,仿真结果取平均值。所提模型的最优调度策略仿真结果见表1。
5.2 结果分析
为了反映不同可靠性指标对系统运行费用的影响,在其他参数不变的情况下,对不同的可靠性要求进行仿真,结果见表2。从表2可知,Emax从0.25%增加到5%,系统的运行费用从$845 536.8下降到$833328.7,降低了1.44%。可以明显看出,Emax越大,系统的运行费用越小,这是因为Emax越大,对系统的可靠性要求越低,则系统的备用越小,从而使运行费用降低。

表1 所提模型最优解对应的各机组有功出力Tab.1 Active power of units corresponding to optimal solution by proposed model

续表

表2 不同的Emax所对应的仿真结果Tab.2 Simulative results for different Emaxvalues
表3描述了不同的V对系统运行费用的影响。由表3可知,当V从500增加到8000时,系统运行费用增大了6.1%。可以看出,系统的运行费用随着V的增大而增加,这是因为,当VOLL增大时,单位缺负荷的费用增加,为了减少缺负荷量,必须增大系统备用,从而导致系统的运行费用增加。

表3 不同的V所对应的仿真结果Tab.3 Simulative results for different V values
运行机组的停运概率和系统的前导时间密切相关,为了模拟不同前导时间对系统运行的影响,本文在其他参数不变的情况下,设置前导时间从1 h到8 h进行仿真分析。从表4可知,随着前导时间的增大,系统运行费用增加。这是因为,当前导时间增大时,机组停运的概率增加,为了满足系统的可靠性要求,必须增加备用,使得系统的运行费用也随之增加。

表4 不同前导时间所对应的仿真结果Tab.4 Simulative results for different lead times
表5反映了风电预测误差随机性的大小对系统运行情况的影响。可以明显得知,预测误差的随机性越大,为了应对这种随机性给系统带来的影响,必须增加备用,从而导致系统运行费用的增加。

表5 不同的风电随机性所对应的仿真结果Tab.5 Simulative results for different swvalues
6 结论
本文提出一种考虑系统可靠性约束的含风电场电力系统动态经济调度模型,并在目标函数中计及中断负荷费用。利用七分段高斯分布模拟负荷和风电预测误差的不确定性。提出一种IPSO算法求解所提模型,该算法引入信息分享和精英学习策略。以IEEE-RTS测试系统为算例,通过仿真分析,验证了所提模型的可行性和有效性,并对影响系统运行的各种因素进行仿真分析,如 Emax、V、TL、sw等。所提模型对于含风电场的调度运行既有理论意义又有实际应用价值。

