风光储独立供电系统电源优化配置
江全元,石庆均,李兴鹏,陈跃辉,张文磊,宋军英
(1.浙江大学 电气工程学院,浙江 杭州 310027;2.重庆市电力公司 长寿供电局,重庆 401220;3.湖南省电力公司,湖南 长沙 410007)
0 引言
因地制宜地发展风能、太阳能等可再生能源发电系统,对于解决山区、牧场、边防、海岛等边远地区人群的用电问题具有重要意义[1-4]。由于风能、太阳能的间歇性和随机性,单独使用风力发电或光伏发电都存在供电不稳定的缺陷,为提高其供电可靠性,通常需配置大量储能装置以动态调整系统的功率偏差。而风能和太阳能在时间及地域上有互补性,白天光照最强时风很小,太阳落山后光照很弱,但由于地表温差变化大而风能加强,夏季太阳光照强度大而风小,冬季太阳光照强度弱而风大。相对于单独使用风力发电或光伏发电,采用风光互补发电形式能获得较稳定的电能,并能在满足相同的供电可靠性的前提下减少储能容量配置需求[4-5]。因此,采用风光储互补发电方案是实现独立供电系统的合理选择,也是解决偏远地区用电问题的有效途径。
电源的优化配置是风光储独立供电系统在规划设计阶段的一个重要内容,其对于减小系统投资成本、提高资源利用率、保证系统供电可靠性等方面具有重要意义。本文在建立基本元件模型的基础上,以系统等年值投资费用最低为目标,考虑系统运行约束条件,构建了风光储独立供电系统的电源优化配置模型,并提出基于粒子群优化算法的数值求解方法。
1 风光储独立供电系统的电源模型
1.1 风光储独立供电系统结构
典型风光储独立供电系统结构见图1。系统中供选择的可再生能源子系统有风力发电机(风机)和光伏发电系统(光伏),供选择的储能设备有蓄电池组和电解槽-储氢罐-燃料电池循环系统,实际系统只能选用一种储能设备进行配置,各电源均直接与直流(DC)母线相连,并通过DC/AC逆变器与交流(AC)母线相连,系统中包含直流负荷和交流负荷。

图1 风光储独立供电系统结构示意图Fig.1 Structure of standalone wind-solar-storage power supply system
1.2 风力发电机输出功率模型
风力发电机的输出功率随风速变化而变化,而风速随高度的增加而变化,气象局提供的风特性数据一般都在9 m高度附近测得。使用时,必须折算成风力发电机转轴高度处的风速,可用指数公式折算[6]:

其中,v、v0分别为 H、H0高度处的风速(m/s);修正指数n与地面平整程度(粗糙度)、大气稳定度等因素有关,取 1/8~1/2,开阔、平坦、稳定度正常地区取 1/7。
风速具有高度的随机性,可通过风速的概率分布来描述其统计特征。双参数威布尔(Weibull)分布被普遍认为是最适用于风速统计描述的概率密度函数,其概率密度函数表达式为[7]:

其中,v为风速;k和c为Weibull分布的2个参数,k称为形状参数,k>0,c称为尺度参数,c>1。k和 c可以由平均风速与标准差σv近似算出:

其中,Γ(·)为 Gamma函数。
当已知风速的分布之后,就可以通过风力发电机组的输出功率与风速间的特性曲线得到风机系统的平均输出功率:

其中,NWG为风力发电机台数;Pw(v)为风力发电机的输出功率与风速之间近似关系(已考虑DC/DC变换器的损耗),可用式(5)所示模型进行描述[8]。

其中,PN为风电机组的额定功率;vc为切入风速;vN为额定风速;vF为切出风速。
1.3 光伏阵列输出功率模型
光伏阵列的输出功率与环境温度及光照强度相关,由于光照强度有随机性,因此输出功率也随机。据统计,在一定时段内(如1个或几个小时)太阳光照强度可近似看成Beta分布,其概率密度函数如下[9]:

其中,G、Gmax分别为一定时间段内的实际光照强度和最大光照强度(W/m2),0≤G≤Gmax;α、β 为 Beta 分布的形状参数,可由一段时间内的光照强度平均值μ和标准差σG得到。

光伏阵列由若干光伏模块经串联和并联组成,单件光伏模块的输出功率可表示为[10]:

其中,PSTC为标准测试条件(STC)下的最大测试功率;l为功率温度系数;ta为环境温度,tNOC为元件额定工作温度(℃)。
在得到光强的分布和光伏模块的输出功率函数后,就可计算光伏阵列平均输出功率:

考虑到光伏阵列表面积尘、最大功率点跟踪控制效率以及DC/DC变换器效率的影响,将光伏发电系统在一定时间段内的平均输出功率表示为:

其中,ηdust为因表面积尘引起的光伏发电系统功率输出效率;ηmppt为最大功率点跟踪控制效率;ηloss为DC/DC变换器效率。
1.4 蓄电池
蓄电池作为储能设备,通过储能控制器可快速地控制其充放电以跟随负荷的变化,在可再生能源充足时,蓄电池充电以储备多余的能量,减少能源浪费,而在可再生能源匮乏时,蓄电池放电为负载提供稳定的电能输出,保障系统正常安全运行。荷电状态、端电压以及寿命周期是蓄电池管理的几个重要参数。
1.4.1 荷电状态
蓄电池荷电状态 SOC可表示为[11]:

其中,σsdr为自放电率;Ibat,t为蓄电池充放电电流,充电时为正,放电时为负;Δt为仿真时间间隔;Cbat为蓄电池安时容量(A·h);Pbat,t为蓄电池的充放电功率,充电时为正,放电时为负;Nbat为蓄电池块数;Ubat,t为蓄电池端电压;ηt为充放电效率,放电时(Ibat,t<0)其值为 1,充电时(Ibat,t>0)与 SOC和充电电流相关,可表示为式(13)[12]。
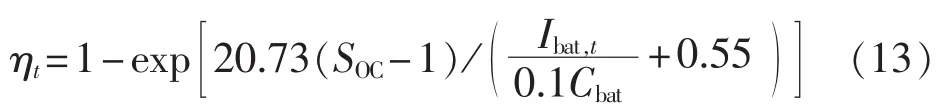
1.4.2 端电压模型
蓄电池端电压可由其开路电压和内阻压降表示为[13]:

其中,Eoc,t为蓄电池的开路电压;Ibat,t为蓄电池充放电电流(大于0表示充电,小于0表示放电);Rbat,t为蓄电池内阻,包括电解质电阻Relectrode,t和电解液电阻Relectrolyte,t两部分;UF为蓄电池满充电压;b、r1、r2、r3、r4为经验系数,在充电和放电模式下具有不同的值。
1.4.3 寿命模型
蓄电池的实际使用寿命与蓄电池的充放电循环周期时间及放电深度有关。本文假设在不同循环周期下,蓄电池的寿命是充放电周期时间内充放电深度的函数。蓄电池寿命的预测是基于图2所示的蓄电池失效循环次数与放电深度的关系曲线。

图2 蓄电池失效循环次数曲线Fig.2 Curve of battery failure cycle times
基于图2中的原始数据,蓄电池失效循环次数可由下式拟合[14]:

其中,CF为蓄电池失效循环次数;DOD为放电深度;a1、a2、a3、a4、a5为拟合系数。
蓄电池寿命损坏期表示为:

其中,Ybat为蓄电池的寿命损坏期(a);Δt为仿真时间间隔;nT为仿真总时段数;SOC1,t、SOC2,t分别为第 t个仿真时段初和时段末的蓄电池荷电状态;Sbat,t为在第t个仿真时段蓄电池的充放电状态,充电时值为0,放电时值为1;DOD,t为在第t个仿真时段末蓄电池的放电深度,DOD,t=1-SOC2,t。
蓄电池的重置周期为:

其中,Ybat为蓄电池的寿命损坏期,Yfloat为蓄电池浮充寿命,由厂家提供。
在系统运行过程中蓄电池将经历充电与放电过程,受其荷电状态允许范围(SOCmin≤SOC≤SOCmax)限制与蓄电池本身技术限制的约束,其最大充放电功率为:

其中,Pmaxch,t、Pmaxdh,t分别为在第 t个仿真时段内蓄电池的最大可充电功率和最大可放电功率;SOCmax、SOCmin分别为蓄电池荷电状态的上、下限;Cbat为蓄电池容量;Ubat,t为蓄电池端电压;Δt为仿真时间间隔;Imaxch、Imaxdh分别为蓄电池允许的最大充电电流和最大放电电流,单位时间内最大充放电电流为蓄电池额定安时容量的 20%[15],如式(24)所示。

1.5 电解槽-储氢罐-燃料电池循环系统
电解槽-储氢罐-燃料电池循环系统在风光储独立供电系统中的作用与蓄电池储能相同:在可再生能源充足的时候,电解槽利用多余的电能电解水,并将电解产生的氢气储存在储氢罐中;而在可再生能源不足时,燃料电池以储氢罐中储存的氢气作为燃料进行发电,以满足系统负荷的需求[16]。
电解槽是一种通过电解水产生氢气的装置,其输出功率可表示为:

其中,Pele-tank为电解槽的输出氢气功率;Pele为输入电解槽的电功率;ηele为电解槽的效率,本文取为75%。
燃料电池以氢气作为燃料进行发电,其输出电功率可表示为:

其中,PFC为燃料电池的输出电功率;Ptank-FC为从储氢罐输入到燃料电池的氢气功率;ηFC为燃料电池的转换效率,本文取50%。
储氢罐中的储能量可表示为:

其中,ηstor为储氢罐的存储效率,本文取95%。
电解槽的最大输出功率受其自身额定功率PNele及储氢罐的剩余储能容量限制:

燃料电池的最大输出功率受其自身额定功率PNFC及储氢罐的剩余储能量限制:

其中,Emaxtank、Emintank分别为储氢罐储能容量的上、下限,取Emaxtank=ENtank,Emintank=0.2ENtank;Etank,t为第 t个仿真时段初始储氢罐剩余容量。
2 风光储独立供电系统电源优化配置模型
2.1 目标函数
本文建立了含有风力发电机、光伏阵列、蓄电池储能装置及电解槽-储氢罐-燃料电池循环系统的独立供电系统的电源优化配置模型,取独立供电系统中光伏电池模块安装块数NPV、风力发电机安装台数NWG、风机塔架高度H、蓄电池块数Nbat、电解槽额定功率PNele、燃料电池额定功率PNFC以及储氢罐的容量Emaxtank为优化变量,主要将设备投资费用、运行和维护费用、设备重置费用3个部分计入目标函数,使系统等年值投资费用ACS(Annualized Cost of System)最低,同时满足用户要求的供电可靠性。独立供电系统电源优化配置模型描述如下:

其中,CACS为系统等年值投资费用;x为优化变量集合,x=[NPV,NWG,H,Nbat,PNele,PNFC,EtNank]T;CCP为安装成本年平均费用;COM为年运行维护成本;CREP为年均重置成本,对于寿命周期时间小于整个项目设计年限的元件需要考虑重置成本。
风光储独立供电系统各元件安装成本年平均费用与元件寿命周期年限相关[13-14]:

其中,CTCP为安装成本;Yproj为元件寿命周期年限;μCRF为资金回收系数 CRF(Capital Recovery Factor),其表达式如式(32)所示。

其中,h为实际利率,与名义利率h′和全年通胀率f有关,其关系满足式(33)。

在项目年限内,若系统元件达到其寿命终止年限,则需要对元件进行重置替换,元件的年均重置成本费用计算公式如下:

其中,CTREP为重置成本;YREP为元件重置周期寿命;μSFF为偿债基金因子,其关系满足式(35)。

2.2 约束条件

其中,RLPSP为负载失电率,为全年运行的系统供电可靠性指标;RL,max为设置的系统可靠性指标;REXC为能量过剩倍率;RE,max为设置的能量过剩倍率限制;Hmax、Hmin分别为风塔设计高度的上、下限;N为非负整数集合;R为实数集合。下文介绍RLPSP及REXC的计算方法。
2.3 储能装置控制策略
因为风能、太阳能资源具有间歇性和波动性的特点,全年独立运行的系统会出现供电小于负荷的情况,这时需要储能装置放电以补充不足电力,另外也会出现供电大于负荷的情况,此时通过储能装置将多余的电能存储起来,以提高可再生能源的利用效率。
本文计算系统1 a的负载缺电概率作为供电可靠性指标。将1 a划分为8760 h,每小时计算一次,在每小时内计算系统各元件的平均功率。
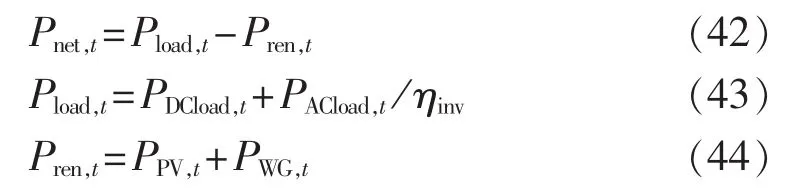
其中,Pnet,t为第 t小时内系统净负荷功率;Pload,t为总负荷功率;PDCload,t为总直流负荷;PACload,t为总交流负荷;ηinv为逆变器效率;Pren,t为可再生能源总发电功率。
系统采用蓄电池或电解槽-储氢罐-燃料电池循环系统作为储能装置时的控制策略分别如下。
a.如果系统采用蓄电池作为储能设备,则当第t小时 Pnet,t>0时,蓄电池放电,蓄电池功率为:


当第 t小时 Pnet,t<0 时,蓄电池充电,蓄电池功率为:


b.如果系统采用电解槽-储氢罐-燃料电池循环系统作为储能设备,则当第 t小时 Pnet,t>0 时,燃料电池发电:

此时若 PFC,t<Pnet,t,表明第 t小时内不能完全满足所有负荷,第t小时的缺电功率为:

当第t小时Pnet,t<0时,电解槽将多余电能转化为氢气以存储:

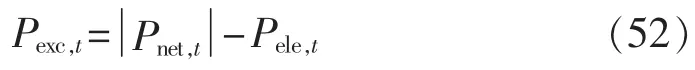
在计算全年各小时内各元件的功率之后,进一步可计算全年缺电概率[13-14]:

其中,SLPSP,t为系统缺电标记符,Punm,t>0 时 SLPSP,t=1,Punm,t=0 时 SLPSP,t=0。
能量过剩倍率定义为在系统全年运行期内过剩的能量除以系统负荷总需求能量,即:

3 基于粒子群优化算法的优化配置
上述独立供电系统电源优化配置是一个多约束条件的混合整数非线性规划问题,尤其是其约束条件中的RLPSP、REXC与优化变量之间难以表示为解析表达式,因此从设计方案寻优的算法上而言只能采用有约束的直接搜索法。本文采用粒子群优化PSO(P article S warm O ptimization)算法求解优化配置模型。PSO算法本质上属于迭代的随机搜索算法,具有并行处理、鲁棒性好等特点,能以较大概率找到问题的全局最优解,且计算效率比传统随机方法高,其最大的优势在于简单易实现、依赖的经验参数较少[17]。
系统优化配置模型的优化变量集合为x,每个优化变量对应粒子的一个维度,即。对于式(36)、(37)体现为相应的优化变量即粒子位置的限制,粒子位置越限时,取其限值。式(40)表明 NPV、NWG、Nbat为整数变量,式(41)表明 H、PNele、PNFC、ENtank为连续变量。对于式(38)、(39)表示的约束,以罚函数形式将其计入目标函数中,即:

其中,σ为惩罚因子。
独立供电系统电源优化配置模型同时包含连续变量和整数变量。对于各粒子的连续变量,其PSO进化方程为:

其中,vid为粒子的速度;xid为粒子的位置;ω为惯性加权;c1、c2为大于零的认知参数和社会参数;r1、r2为(0,1)均匀分布的随机数;pid为粒子自身经历的最好位置;pgd为微粒群中所有粒子经历的全局最好位置。
对于各粒子的整数变量,其PSO算法可形式化描述为[18]:

其中,φ1є[a1,b1]等概率分布的整数,φ2є[a2,b2]等概率分布的整数,并且满足式(60)。

针对风光储独立供电系统的电源优化配置问题,本文采用PSO算法求得优化配置结果的流程,如图3所示。
4 算例分析
4.1 基础数据

图3 求解系统电源优化配置问题的PSO流程图Fig.3 Flowchart of PSO for optimal DG configuration model
应用本文方法对独立供电系统的电源进行优化配置,备选的分布式电源类型有风力发电机、光伏模块、蓄电池、电解槽、储氢罐和燃料电池。风力发电机参数:PN=30 kW,vc=3 m/s,vN=11 m/s,vF=25 m/s。光伏电池参数:PSTC=100 W,tNOC=44.2℃,k=-0.4%,ηdust=94%,ηmppt=96%,ηloss=96%。蓄电池参数:Cbat=100 A·h,额定电压为12 V,允许放电深度DOD=80%,失效循环次数为560,浮充寿命为8 a。风机塔架高度的上、下限分别设为15 m、8 m,各种电源及系统其他元件的成本参数如表1所示,项目设计年限定为20 a。以上基本数据综合取自文献[11-14],算例中暂按美元与人民币汇率1∶6.38折算后进行相关计算。由表1可见,各系统元件中只有燃料电池的寿命低于项目设计年限,蓄电池的寿命与系统配置和全年实际运行状态相关,其寿命可能低于项目设计年限,因此燃料电池和蓄电池涉及重置费用。
独立供电系统容量优化配置还需工程所在实地的典型年气象数据和负荷数据。气象数据包括小时平均风速、风速标准差、小时平均光照强度、光强标准差、小时最大光强及小时平均环境温度,负荷数据包括小时平均直流负荷和小时平均交流负荷。设计2个算例,其中算例1所用气象、负荷数据如图4、图5所示,算例2所用气象、负荷数据如图6、图7所示。
针对每一算例计算2种方案:
a.方案1,备选电源只考虑风机、光伏阵列、蓄电池,即风/光/蓄电池独立供电系统;
b.方案2,备选电源只考虑风机、光伏阵列、电解槽-储氢罐-燃料电池循环系统,即风/光/循环储能设备的独立供电系统。
2种方案均考虑风光储独立供电系统的最大允许缺电概率RL,max分别设置为0%、1%、2%的情况,RE,max均设为 100%。

表1 独立供电系统元件参数Tab.1 Component parameters of standalone power supply system

图4 算例1中独立供电系统所在地的气象数据Fig.4 Meteorological data for standalone power supply system of case 1

图5 算例1中独立供电系统所在地的全年负荷数据Fig.5 Annual load data for standalone power supply system of case 1
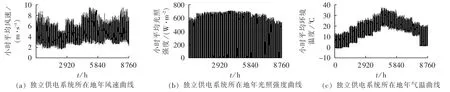
图6 算例2中独立供电系统所在地的气象数据Fig.6 Meteorological data for standalone power supply system of case 2

图7 算例2中独立供电系统所在地的全年负荷数据Fig.7 Annual load data for standalone power supply system of case 2
4.2 结果分析
采用提出的独立供电系统电源优化配置方法,得到电源优化配置结果如表2和表3所示。
对比分析两算例中方案1和方案2下的优化配置结果易知,显然采用方案1更经济,原因分析如下:方案2采用电解槽-储氢罐-燃料电池循环系统作为储能装置,其储电和发电是通过不同元件实现的,这无疑增加了系统投资成本,相对于方案1采用单一元件的能量可双向流动的蓄电池储能形式,循环系统储能形式的单位储能量对应的投资成本要高得多。因此,在满足相同供电可靠性的前提下,方案1比方案2的最优配置更经济。将电解槽-储氢罐-燃料电池循环系统仅作为独立供电系统中的电储能转换装置是不经济的,但是燃料电池系统可实现(冷)热电联供,提高燃气能量转换效率,在同时有电负荷和热(冷)负荷需求的地区,才能体现方案2的相对优势。

表2 算例1中独立供电系统电源优化配置结果Tab.2 Result of configuration optimization for standalone power supply system of case 1

表3 算例2中独立供电系统电源优化配置结果Tab.6 Result of configuration optimization for standalone power supply system of case 2
由于算例2中的年风速水平和年光照强度水平均偏低,而负荷水平更高,因此算例2中系统优化配置下的等年值投资费用更高。
从方案1和方案2的优化配置结果能得到一个共同的结论:可靠性指标设置得越高(即RL,max设置得越小),则独立供电系统的年投资费用越高,高供电可靠性会带来高经济性代价。因此,合理地评估停电损失和设置可靠性指标是降低系统电源冗余投资的有效手段之一。
5 结论
a.在仅有电负荷需求的边远地区,由风/光/蓄电池构成的独立供电系统比由风/光/燃料电池循环系统构成的独立供电系统的优化配置更为经济;
b.合理地评估停电损失和设置可靠性指标可有效降低风光储独立供电系统冗余投资;
c.燃料电池系统可实现(冷)热电联供,提高燃气能量综合转换效率,对于同时有电负荷和热(冷)负荷需求的地区,分别采用电解槽-储氢罐-燃料电池循环系统与蓄电池作为储能形式时的经济性配置有待进一步研究。

