基于同配性的电力系统自组织临界性识别
曹一家,张宇栋,林 辉,韩浩江,包哲静
(1.浙江大学 电气工程学院,浙江 杭州 310027;2.湖南大学 电气与信息工程学院,湖南 长沙 410082;3.上海市电力公司市北供电公司,上海 200011)
0 引言
近年来,复杂系统理论作为一种新兴的交叉理论,引起了国内外研究者的普遍关注和重视,其中最具代表性的成果之一是大停电自组织临界理论SOC(Self-Organized Criticality)[1]。对于一个耗散动力系统,其通过自组织过程,自发地向系统的临界状态演化。处在临界态的系统受到任何一个微小扰动都可能引起灾变的发生,并且灾变发生的规模和相应的累积概率之间呈现幂律(power-low)分布而非指数分布,这也被认为是自组织临界性的数学表征,此时系统大规模灾变的发生概率不可忽略。已有研究通过分析美国和我国的历次停电数据[2-3],验证了美国和我国电力系统停电规模与其频次间满足幂律关系,说明国内外电力系统均存在自组织临界性。目前关于电力系统自组织临界性的研究主要从2个角度进行:一是建立电力系统的长期演化模型,仿真得到停电数据加以分析,其中应用最广泛的是OPA模型[4];二是建立电力系统某一运行断面下的连锁故障模型,如隐性故障模型[5],通过仿真得出该运行状态下的停电数据,绘出停电分布曲线,以此判断该状态下系统是否已经自组织到临界状态。考虑到调度人员较关注系统目前的运行状态是否处于危险状态,本文主要从第2种角度出发,对系统当前运行状态进行识别,并判断系统是否已进入临界状态。
文献[6-7]指出系统的平均负载率是决定系统是否处于自组织临界态的主要因素,当系统线路平均负载率处于高位时,系统可能处于临界状态。如文献[6]指出,线路平均负载率为0.79时,系统处于自组织临界态。但是文献[8]的研究表明,我国华北电网在2005年夏大运行方式下,线路平均负载率处于0.278时就进入了临界状态。各研究结果之间的巨大差异显示,线路的平均负载率并不是决定系统自组织临界性的唯一指标。文献[9-10]分析了线路潮流的分布特性对连锁故障的影响,发现潮流分布的不平衡性也是决定系统是否处于临界状态的重要因素。但是,文献[9-10]在设置指标时,只是研究了线路负载率在宏观上的分布情况,并未考虑每条线路个体对系统的重要程度的差别。然而以往的研究[11]表明,不同线路对系统的影响往往具有较大的差别,即电力系统中各条线路的脆弱程度[12]不同。
因此,本文在设置指标时,充分考虑了线路在潮流转移中的作用,并利用复杂系统同配性(assorta-tivity)的概念对线路脆弱性和负载率的匹配程度进行量化,以此建立线路同配性指标来度量线路潮流分布特性。最后应用此指标分析了潮流分布特性对电力系统自组织临界性的影响,并结合平均负载率和潮流熵验证了该指标对于识别系统自组织临界状态的有效性。
1 线路同配性
文献[9-10]提出的相关指标,本质上描述的都是线路负载率在一系列给定区间下的分布情况,并不涉及负载率与其脆弱性的匹配情况。因此,本文提出电力系统线路同配性指标的主要思路为:首先基于潮流转移增量[13]对线路的脆弱性进行评估,再划分线路脆弱性等级,然后对线路负载率划分相应等级,最后利用同配性概念对线路的脆弱性和负载率的匹配程度进行量化。
1.1 基于潮流转移的线路脆弱性评估
研究表明,电力系统连锁故障的主要原因是有功潮流的大规模转移。当系统一条或多条线路断开时,线路潮流发生转移,某些线路上的潮流可能因超过其传输极限而发生跳闸,随后引起新一轮的潮流转移,逐渐形成连锁故障。因此,线路开断引起的线路潮流增加量是评估线路脆弱性的一个关键指标,本文基于线路潮流的增量对线路脆弱性进行评估。
1.1.1 潮流转移增量
定义Δk-l为线路l的开断造成线路k潮流增大量,线路k潮流的增大方式包括正向增加和反向增加。对于给定的电力系统运行状态,线路l的开断造成线路k潮流的变化量可以方便地由支路开断分布因子[14]算出。因此,本文利用支路开断分布因子来计算线路的潮流转移增量。假设所有线路的初始潮流方向为正方向,线路l的初始潮流为Fl,线路l开断造成线路k潮流的变化量为ΔFlk,则:

其中,Dk-l为支路开断分布因子,其物理意义是线路l断开后线路k上的潮流变化量占线路l初始有功潮流的百分比。
当Dk-l>0时,表示线路k的潮流正向增加,线路l的开断造成线路k潮流的增大量Δk-l为:

当Dk-l<0时,表示线路l的开断对线路k潮流有减小作用,当时,线路 k 的潮流发生反向,并且当时,线路 k 的潮流反向增加,其增大量Δk-l为:

如果线路l的开断并没有引起线路k潮流的增加,本文认为Δk-l=0。
1.1.2 线路脆弱性综合指标
以往对于线路脆弱性的研究,大多仅考虑线路退出运行后对系统造成的影响,而忽略了线路自身的抵抗能力。若线路自身抵抗潮流冲击的能力很强,那么该线路将不易出现退出运行的情况,故其对于整个系统中其他线路的影响将受到很大限制。因此,本文提出的线路脆弱性包括2个方面:一是该线路退出运行后,对系统其他线路的冲击大小;二是系统其他线路退出运行后,该线路受到冲击的大小。
本文将线路l的第1种脆弱性指标用V1l表示,定义其初始值为:

其中,M表示系统的线路数,线路l脆弱性的初始值并未考虑线路的连锁故障风险。假设线路l断开后自身线路潮流增大的线路集合为Sl,如若发生进一步的连锁故障,集合Sl中每条线路的断开对其余各条线路的影响程度可能各不相同,那么在获取线路l的第1种脆弱性时,应充分考虑这种影响的差异。因此,本文采用迭代的方法对线路初始脆弱性进行修正,其迭代公式为:

线路l的第2种脆弱性指标度量的是其余线路开断对其自身的潮流冲击,记为V2l。线路受到的潮流冲击应分为全局冲击和局部冲击,全局冲击度量的是其余所有线路开断引起的潮流冲击在该线路上的叠加,局部冲击度量的是该线路受到的最大潮流冲击。为简化指标,本文认为这2种冲击的权重相同,故V2l的计算公式为:

综合分析上述2种脆弱性指标,一方面,虽然线路自身的开断可能对其余多数线路都有较大影响,但是该线路自身抵抗潮流冲击的能力很强,不易出现过载而切除,那么它对其余线路的影响将受到一定的限制;另一方面,虽然线路可能因自身抵抗冲击潮流能力弱而频繁发生开断,但是其开断可能对其余线路影响甚小,那么此类线路也不是最脆弱的线路。那么,单独考虑任何一种脆弱性指标都是不科学的。因此,本文结合上述2种指标提出了线路脆弱性综合指标。为了消除不同指标间取值的差异,首先对V1l和V2l进行归一化处理,那么线路l脆弱性综合指标为:

综上所述,本文提出的脆弱性综合指标的物理意义为:线路受到的冲击越大,且断开后对其余线路影响越大,该线路越脆弱。为了使线路脆弱性结果更加直观,本文亦对Vl进行了归一化处理。
1.2 网络同配性
复杂网络具有多种特殊性质,其中重要的一种就是同配性。简单而言,可以将“同配性”解释为“物以类聚、人以群分”,具有相似经历、背景、知识水平等社会属性的人往往倾向于聚在一起。
复杂网络同配性描述的是节点间的相关性,若网络中的节点倾向于和它度数相近的节点相连接,如低度数节点趋于和低度数节点相连,高度数节点趋于和高度数节点相连,那么称该网络具有同配性。
M.E.J.Newman为定量研究网络的同配性,在文献[15]中定义了测量网络同配性的方法,提出了同配性系数的概念,该系数定义为:
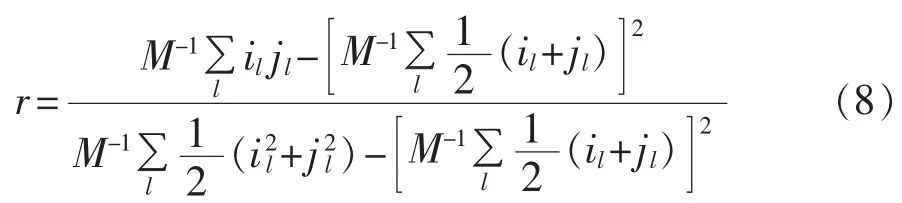
其中,il和jl分别为线路l两端节点各自的度数;M为网络中边的数目;r为网络的同配性系数,且r є[-1,1]。当r>0时,表示整个网络中的高度数节点倾向于和高度数的节点相连;当r<0时,表示高度数节点倾向于和低度数节点相连;当r=0时,表明网络中的节点是随机连接。
1.3 线路同配性指标
式(8)所定义的网络同配性系数度量的是线路两端节点度的匹配程度,而本文的目标是对线路的负载率和脆弱性这2种属性的匹配程度进行量化,并以此建立电力系统的线路同配性指标。显然,线路两端的节点度量程相同,而线路负载率与其脆弱性的量程却存在很大差异。所以为了便于应用式(8)计算线路同配性,本节将线路负载率和脆弱性划分为5个等级,以此实现这2种属性在量程上的统一。但是,线路负载率或者脆弱性指标是连续变化的,那么仅将其重要程度划分为5个离散的等级区间,并不能很好地反映这2种属性变化的连续性。因此,本文认为线路的负载率或者脆弱性等级可以取5个离散等级之间的任意一个实数。
1.3.1 线路负载率和脆弱性的等级划分
线路负载率和脆弱性在较小时,对整个系统的影响很小,此时若详细区分这2种属性的等级,不仅增加计算量,而且实际意义不大。并且,在电力系统实际运行时,高负载率和高脆弱性的线路亦不常见。因此,本节对负载率等级进行划分时作了如下简化:当线路负载率小于某一阈值a时,其重要等级为1;当负载率大于某一阈值b时,其重要等级为5。而当负载率处于这2个阈值之间时,其重要等级呈线性分布,具体如下:

其中,μl为线路 l的负载率;Rμl为其对应的重要等级。
参照线路负载率的等级划分方法,本文在对脆弱性重要程度划分时,也将中间范围的等级作了线性简化,假设其等级划分由式(10)计算:

1.3.2 线路同配性指标
参照式(8),本文的线路同配性指标(记为A)如式(11)所示:

其中,M 为系统中总的线路数;Aє[-1,1]。当 A>0时,表示系统中线路的负载率越高,其自身的脆弱程度也越高;当A<0时,系统中线路的负载率越高,其自身的脆弱程度越低;当A=0时,说明系统中线路的负载率跟其脆弱程度是随机匹配的。
1.3.3 不同线路同配性指标的获取
本文的研究重点是线路同配性指标对电力系统自组织临界性的识别作用。由于线路的平均负载率和潮流熵(潮流分布的不平衡性)也对系统自组织临界态有重要影响,所以为了消除线路平均负载率和潮流熵对仿真结果的影响,需要在同一平均负载率和潮流熵下生成不同的线路同配性指标值。同配性指标的计算涉及线路负载率和线路脆弱性2个方面,若此2个方面同时变化将不利于同配性指标的生成。故本文采用了更为简单易操作的方法:首先保持各节点注入功率不变,这样线路脆弱性指标将不会发生变化,然后通过调节各条线路的最大有功传输极限Fmaxl来改变线路的负载率(与负荷波动导致的线路负载率变化效果一致),并以此来生成不同大小的线路同配性指标。对于给定的平均负载率μ和潮流熵H,不同的线路同配性指标生成步骤如下。
a.生成一组数量为M(线路总数)、期望为μ、方差为 σ 的正态分布的随机数,即 μl~N(μ,σ)。
b.为保证随机数组的平均数值为μ,应对生成的数组进行修正,假设修正后的 μl用 μ′l表示,则:

c.不断调节σ的大小生成不同的随机数组。当生成的随机数组的熵等于给定潮流熵H,固定该随机数组。此时系统的潮流熵等于给定潮流熵。
d.将生成的随机数组中的每一个数值随机赋给系统中的一条线路作为其负载率,假设将μ′l赋给线路l,则其最大传输极限应为:

其中,Fl为线路的初始潮流。由于每条线路的脆弱性固定,所以通过改变随机数组中各元素与线路的对应关系可以获得同一平均负载率和潮流熵下,不同的线路同配性指标。
需要注意的是,潮流熵和线路同配性的取值并不是独立的,而是相关的。例如,当H=0时,每条线路的负载率都相等,同配性指标不可调,是一个固定值。但是,潮流熵越大,线路的负载率分布的区间越广,因此线路同配性可调节的空间越大,取值范围也越广。
2 仿真结果分析
本文采用文献[16]建立的OPA模型快动态过程作为连锁故障的仿真模型,对电力系统的连锁故障进行仿真,研究线路同配性指标对电力系统连锁故障自组织临界态的影响。
由文献[10]的研究结果可知,当线路的平均负载率为0.8时,即使潮流熵为0(各条线路的负载率都为0.8),电力系统也表现出了自组织临界性。即在平均负载率较高的情况下无需设置其他任何指标,仅从平均负载率的角度也可揭示系统的自组织临界性。考虑到本文设置线路同配性指标的目的是在较低平均负载率下完成系统自组织临界状态的识别,所以为了确认本文的研究范围,首先假设每条线路的负载率都相同,令线路平均负载率分别为0.6、0.7和0.8,并在新英格兰39节点系统中进行10000次连锁故障仿真,每次随机选取1条线路断开,图1给出了其负荷损失累积概率P(X>x)在双对数坐标下的分布情况。

图1 不同平均负载率μ下的负荷损失累积概率分布Fig.1 Log-log plot of probability vs.load loss at different μ
如图1所示,当系统平均负载率μ为0.7和0.8时,其负荷损失的累积概率分布曲线的尾部近似为一条直线,呈现比较明显的幂律特征,此时系统处于临界状态。而当μ=0.6时,其负荷损失概率分布曲线的尾部迅速下降,没有幂律特征,系统尚未进入自组织临界状态。因此,本文在研究线路同配性对自组织临界态的影响时,仅分析线路平均负载率在0.6以下的情况。同时,为验证线路同配性指标的有效性,本文分别在新英格兰39节点系统和IEEE 118节点系统下对连锁故障过程进行仿真。
2.1 新英格兰39节点系统
在新英格兰39节点系统中,等级划分的边界值取值如下:a=0.5,b=0.9,c=0.01,d=0.1,e=0.9。为研究线路同配性大小和自组织临界性的对应关系,图2给出了线路平均负载率μ=0.5、潮流熵H=3.3情况下,线路同配性 A分别为-0.4、-0.2、0、0.3和0.6时的负荷损失累积概率P(X>x)的分布曲线。

图2 新英格兰39节点系统μ=0.5、H=3.3时不同线路同配性下的负荷损失累积概率分布Fig.2 Log-log plot of probability vs.load loss at different A when μ=0.5,H=3.3 for New England 39-bus system
如图2所示,随着线路同配性指标的不断增大,电力系统的大规模停电故障概率在逐渐升高。当A≤0.3时,其负荷损失概率分布曲线的形状大致相同;但当A=0.6时,分布曲线形状发生了很大变化,其尾部呈现明显的幂律特性,表明系统自组织到了临界状态。在仿真过程中,本文虽然保持系统的平均负载率和潮流熵不变,但是负荷损失概率分布曲线却并不相同,甚至在同配性指标较大时,系统出现了自组织临界性。这表明,无论是平均负载率还是潮流熵,其在识别系统临界状态时具有局限性,线路同配性是以上2个指标的重要补充。结合平均负载率和潮流熵,线路同配性指标对系统的状态有较好的指示作用。当系统的潮流熵较大时,若线路同配性指标很小,调度人员仍可以认为系统运行在安全状态;而当同配性指标较大时,调度员应采取相关措施,降低线路同配性,使系统远离临界状态。
图2所进行的仿真的潮流熵处于高位,为验证线路同配性指标在潮流熵较小时的有效性,对照系统在μ=0.5、H=3.3时的停电分布,改变潮流熵为2.12,在相同平均负载率下,同样取线路同配性分别为 -0.4、-0.2、0、0.3 和 0.6,并给出其负荷损失累积概率分布曲线如图3所示。需要指出的是,为保证同配性指标的大范围分布,在平均负载率为0.5时,潮流熵的最小值为2左右,无法无限制地降低。

图3 新英格兰39节点系统μ=0.5、H=2.12时不同线路同配性下的负荷损失累积概率分布Fig.3 Log-log plot of probability vs.load loss at different A when μ=0.5,H=2.12 for New England 39-bus system
如图3所示,在不同潮流熵下,随着同配性的不断增大,大规模停电故障概率的变化趋势基本与图2保持一致,并且同样在同配性为0.6时,曲线尾部近似为一条直线,系统自组织到临界状态。这表明,线路同配性指标在不同潮流熵下,对系统的自组织临界性仍有较好的识别能力。特别地,本文在图2和图3的基础上比较了新英格兰系统在μ=0.5、A=0.6时,不同潮流熵下的负荷损失概率分布曲线。如图4所示,保持平均负载率和线路同配性指标不变,系统在不同的潮流熵下负荷损失概率分布曲线的差别不大。因此,同配性指标在不同的潮流熵下仍具有效性。

图4 新英格兰39节点系统μ=0.5、A=0.6时不同潮流熵下的负荷损失累积概率分布Fig.4 Log-log plot of probability vs.load loss at different H when μ=0.5,A=0.6 for New England 39-bus system
为验证线路同配性指标在不同平均负载率下的有效性,图5对比了线路同配性指标为0.6,平均负载率分别为0.3、0.4和0.5时的负荷损失概率分布曲线。如图5所示,当A=0.6时,系统在3种平均负载率下的曲线尾部都近似为一条直线,系统呈现明显的临界状态。特别地,当μ=0.3时,尽管系统的小规模故障的概率较小,但是其大规模故障却出现了幂律尾。这表明,线路同配性指标在平均负载率较低的情况下仍能很好地辨识系统的自组织临界状态。

图5 新英格兰39节点系统A=0.6时不同平均负载率下的负荷损失累积概率分布Fig.5 Log-log plot of probability vs.load loss at different μ when A=0.6 for New England 39-bus system
2.2 IEEE 118节点系统
在IEEE 118节点系统中,等级划分的边界值取值如下:a=0.5,b=0.9,c=0.001,d=0.01,e=0.8。
图6给出了线路平均负载率μ=0.5、潮流熵H=2.9,线路同配性 A 分别为 -0.6、-0.3、0、0.3和 0.6时的负荷损失概率分布曲线。如图6所示,随着线路同配性指标的增大,系统的大规模故障的概率逐渐升高,并且同样在A=0.6时,分布曲线的尾部呈现较明显的幂律特性,系统自组织到了临界状态。

图6 IEEE 118节点系统μ=0.5、H=2.9时不同线路同配性下的负荷损失累积概率分布Fig.6 Log-log plot of probability vs.load loss at different A when μ=0.5,H=2.9 for IEEE 118-bus system
图7给出了线路同配性指标为0.6,平均负载率分别为0.4、0.5和0.6时的负荷损失概率分布曲线。如图7所示,即使改变了仿真算例,同配性指标在不同负载率下也能很好地识别系统的自组织临界性。结果表明,本文提出的线路同配性指标有较好的普适性,通过调节等级划分的边界值可以适应不同系统辨识自组织临界状态的需求。

图7 IEEE 118节点系统A=0.6时不同平均负载率下的负荷损失累积概率分布Fig.7 Log-log plot of probability vs.load loss at different μ when A=0.6 for IEEE 118-bus system
本文也改变系统的初始状态进行了多次仿真实验,虽然系统自组织到临界状态时的线路同配性指标的具体取值不同,但是线路同配性指标越大、系统的自组织临界性越明显的规律是一致的。特别当系统平均负载率和同配性指标同时处在较高水平时,调度员应采取措施,在安全运行的基础上改变系统潮流分布,降低线路同配性指标,使系统远离临界状态。
3 结论
本文利用复杂理论中同配性的概念,通过定义线路同配性指标,匹配了线路的负载率和脆弱性,并结合线路平均负载率和潮流熵对电力系统的自组织临界性进行了识别。仿真结果表明,线路同配性指标在多个电力系统的不同平均负载率和潮流熵下都能较好地揭示系统的自组织临界性;并且线路同配性指标在系统平均负载率较低时仍有较好的识别临界状态的能力。线路同配性指标的提出是对现有预防大停电的指标的重要补充,并且对调度员的安全调度具有一定的指导意义。

