随机利率下寿险定价分析

张 倩

(哈尔滨商业大学金融学院，黑龙江哈尔滨150028)

随机利率模型指在一段时间内，为了研究利率的随机波动而建立的模型。主要分为均衡利率模型和无套利利率模型。

随机利率的建模大多采用利息力累计函数建模，利息力累计函数一般定义为Y(t)=δt+Zt，其中Zt是随机过程，δ为与t无关的随机变量或常数。

目前国内的精算研究人员对随机利率寿险问题进行了卓有成效的研究，构建了许多具有较高参考价值的寿险模型，但是在实际应用中这些模型仍然存在一些缺陷，迫切需要运用精算技术改进模型以增强模型的实用性。本文以此为研究目标，根据近年来国内外对随机利率的研究成果，建立随机利率模型，研究纯保费的计算。

David Perry(2001)将随机利率采用反射Brownian运动建模，给出一定确定年金的期望值，在Zt为非负数时可以符合利息为非负时的情形，适合在2004年10月24日以前应用。此前保险公司的资金运用限于在银行存款，买卖政府债券、金融债券和国务院规定的其他资金运用形式，Zt不可能为负。

2004年10月24日，中国保监会和证监会共同制定了《保险机构投资者股票投资管理暂行办法》，该《办法》明确规定了保险资金的入市方式，规定保险公司委托保险资产管理公司进行股票投资，或保险公司以内设资金运用部门进行股票投资两种管理方式。如果保险公司将保费收入投资到股市中，Zt随着股价升降而变化，则有可能为负。基于保险资金运用形式放宽条件下考虑，Zt是于0—U过程或wiener过程比较合理。本文假设Zt是Wiener过程 。

一、模型建立

假设x岁的投保人购买了保额为b个单位的n年定期寿险，缴费期为n年，每年所交的均衡纯保费为P。该模型具有如下特征:

1.模型中被保险人缴纳的只是纯保费，未考虑寿险公司的费用和利润因素，所依据的原理是“精算等价原理”。

2.一般情况下，当被保险人死亡时，从申请理赔到保险公司确认理赔，再到保险金的最终给付需要一定时间，这里不考虑此时间差异。

3.对利息力采用标准Wiener过程建立一个半连续情形下随机利率的模型，即死亡给付在被保险人死亡时支付且保险费是期初付生存年金的方式缴纳。

4.死力采用De－Moivre在1972年提出生存时间在［0，ω] 上均匀分布，ω表示人类寿命的极限。

本文对随机利率采用多数文献中的一般标准Wiener过程建模，建立利息力积累函数y(t):

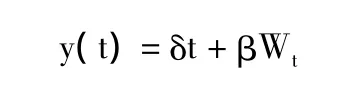
其中，δ为与t无关的随机变量或常数;

W(t)为标准Wiener过程;

β≥0，δ，W(t)相互独立。

此利息力累计过程分为两个部分:1.δt是利息力累计中确定性的部分，瞬时的收益率为δ;2.βWt为考虑利率波动性的部分，由于 E［Wt]=0，Var［Wt]= σ2t，即时间越长，波动性越大。

对于一个单位的资金，可得在t时刻的贴现函数为:

(1)均衡纯保费

半连续式寿险模型是保险实务中最常用的保险模型。对于保险金额为1个单位的半连续式普通n年定期寿险，若被保险人在签单时年龄为x岁，投保n年期定期寿险，其年缴纯保费用符号)表示，根据这一平衡原理，得出:

用符号 表示第k年度此寿险保单的责任准备金，根据未来法，责任准备金的计算原理是未来保险利益在结算日的精算现值减去未缴保费在结算日的精算现值，即

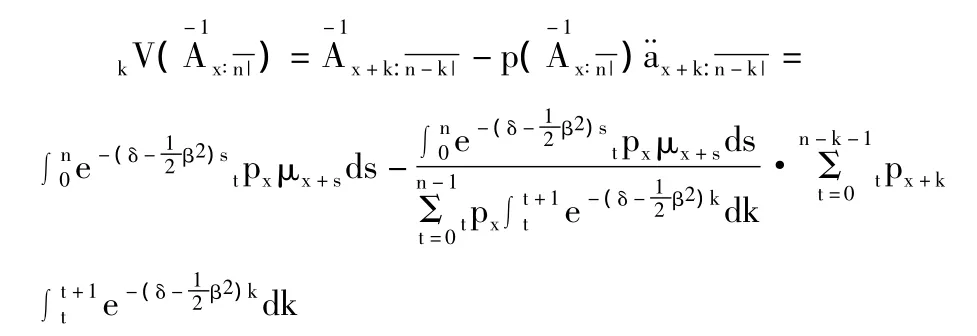
在死力服从De－Moivre形式的假设下

在以上分析中，主要是对利息力模型进行推敲，首先建立利息力的维纳过程模型，计算未来价值的精算现值。然后根据价值理论，就寿险精算问题中投保人和保险公司所关注的保费及准备金和准备金风险进行分析。

由以上计算可以得出，寿险的纯保费和责任准备金主要由被保险人的年龄、保险种类、保险金额、死亡率和利率因素决定。一般情况下，被保险人的年龄、保险种类、保险金额在被保险人投保时已经确定，死亡率采用的是生命表所提供的死亡率水平，并且这一死亡率水平通常在一定时期内相对稳定，因此影响寿险纯保费和责任准备金的主要因素就是利率。这里分析的利率变化对寿险纯保费的计算和责任准备的提留的影响有很大的实用价值。

二、结论

寿险产品具有保障性和储蓄性双重特点，产品先出售而后有成本核算。在产品定价中采用的是精算平衡等式，对预定利率进行核算，而预定利率是一个假设性利率，在若干年以后会出现和真实利率的差异，这是造成寿险公司盈利或者亏损的原因之一。

面对银行存款利率的不断下调，寿险公司为了保持自身的盈利状况，也降低了预定利率，但之前发售的高利率保单合同已经成立，无法进行回溯修改，于是寿险公司背负了沉重的利差损。高盛的一份报告提出，中国人寿、平安、太平洋人寿三大寿险公司的潜在利差损为320亿～760亿元人民币。

本文对于寿险中人的死亡率因素主要参考了现有的生命表，生命表在此就代表了随机死亡率，但是生命表的构造并不代表所有人群的死亡特征，所以可以从人口模型上考虑这一因素，从理论上进一步丰富随机死亡率的研究，并运用到寿险精算当中。

利率在寿险定价时是一个非常重要的参数。如果采用的定价利率过低，保费偏高。虽然保险人会获得更多利润，但较高的保费不利于吸引更多的顾客;定价利率过高，保费偏低。保险人的投资收入难以平衡其给付。

利率波动对寿险定价的影响所带来的风险实质上是寿险产品定价时预定利率与市场利率发生偏差时带来的风险。而利率变动的长期趋势是不确定的，这是寿险产品长期定价短期计量矛盾带来的风险。

寿险公司利率波动的风险主要反映在两个方面:一是保险公司在融资和投资的过程中，由于利率变动增加成本或者使收益率下降，使寿险公司预期利润难以实现。二是利率变动使寿险公司资产和负债的价值造成不同影响，导致资产和负债不匹配的风险。比如，当利率上升时，资产和负债都会下降，但资产价值下降超过负债价值的下降;当利率下降时，资产上升小于负债价值上升，这些都会影响保险人的偿付能力。

［1] 卢仿先，张琳.寿险精算数学［M] .北京:中国财政经济出版社，2006.

［2] 李秀芳.我国寿险业的利率风险分析及其防范［J] .南开经济研究.2000(1).

［3] 周伏平.利率与寿险精算模型的改进［J] .统计与精算，2004(4).

［4] 周宏波，叶俊.随机利率下的生存年金模型［J] .理论新探，2005(4).