“回”型运动枪机退壳动作故障预测分析

仲其伐，李忠新，郝光荣

（南京理工大学机械工程学院，江苏南京 210094）

0 引言

突击步枪是应战争发展要求而产生的新型单兵武器。它成功地结合了冲锋枪与传统步枪特有的最佳战斗性能。现在的突击步枪具有射速高、后坐适中、动作稳定、枪体小而轻便的特点。大量的事实表明，现代突击步枪并非是单纯随着战术变化而变化的，而是随着科学技术的不断进步而逐渐发展起来的一种新型单兵武器。时至今日，现代突击步枪已经从过去仅能杀伤点目标的单兵装备，发展成如今同时具备点面杀伤功能、能够不分昼夜持续使用的单兵多功能综合战斗系统［1］。目前世界各国军队都把突击步枪作为步兵的重要武器装备，因此突击步枪的研制水平和使用性能会直接影响士兵的战斗能力和存活机率，也在某种程度上决定了最终的战斗结果。

本文所研究的新型突击步枪沿用了美国人提出的“齐射”理念，利用了AN94的关键技术思想，并采用了独特的“回”型运动枪机和一些创新结构，力求使其在采用传统步枪原理的基础上，具有极好的首发命中精度和综合作战性能。此外，由于该突击步枪正处于方案研究阶段，缺少相关的试验验证，所以在此阶段对该枪进行故障预测分析既可以及早发现和解决潜在问题，又可以为方案改进工作提供一定的数据和技术支撑。

1 “回”型运动枪机工作原理

“回”型运动枪机是指在整个自动循环过程中，枪机的运动导引会沿着机匣上的“回”字形导轨槽运动，故称之为“回”型运动枪机。就其主要功能而言，“回”型运动枪机其实是一种枪机偏转式的单程进弹机构，即枪机在整个运动过程中会产生偏转运动以便于顺利地完成整个供弹动作，“回”型运动枪机的基本结构如图1所示。

图1 “回”型运动枪机的基本结构

2 “回”型运动枪机退壳动作可能出现的故障

在“回”型运动枪机完成退壳动作的过程中，有可能会出现下列故障:1）弹壳横向断裂;2）弹壳纵向破裂;3）卡壳。

根据自动武器的基本特性可知，在枪机完成退壳动作过程中，弹壳容易发生横向断裂和纵向断裂故障。其中，横向断裂是指为了保证弹壳向后推动枪机有足够的能量，作用于弹壳底部的火药燃气压力必须大于弹壳外壁与弹膛间的摩擦阻力，然而该摩擦阻力可能大于弹壳在拉断前所能承受的极限拉力，从而导致弹壳被过度拉伸而拉断;纵向破裂是指因高膛压时期弹壳后移量过大时，弹壳底部径向薄壁失去弹膛支撑，或者是因弹壳锥度过大或为瓶形，其向后移动时肩部或体部与弹膛壁间出现较大间隙，导致弹壳发生炸裂或破裂［2］。另一方面，由于所述突击步枪采用的抛壳挺簧式弹性抛壳机构，其抛壳动作依靠抛壳挺簧作用在弹壳上的抛壳力矩来完成。该类抛壳机构的主要优点是抛壳动作平稳无撞击且结构简单易加工，而其缺点则在于枪机结构对抛壳机构尺寸有限制，抛壳能量不会太大，另外各机构间的位置间隙、抛壳窗位置尺寸以及枪机后坐速度等因素也会对抛壳产生影响。一旦抛壳出现问题，就极容易引发卡壳故障。由于篇幅所限，本文对卡壳故障预测分析将不予论述。

3 弹壳强度故障分析

“回”型运动枪机采用自由枪机式自动原理，其枪机与枪管或机匣之间没有扣合，因此当枪弹被击发后，在弹头还未完全嵌入膛线时，枪机便已经开始后坐。由于在枪弹被击发的瞬时，枪机并没有得到刚性闭锁支撑，故当膛压达到一定值后，准确的说，是当膛底火药燃气压力合力超过枪弹拔弹力时，弹壳便可带动枪机共同后坐。由此可知，“回”型运动枪机没有专门的闭锁机构，其闭锁方式属于惯性闭锁［3］。

根据膛内弹壳的受力特点，可建立发射时弹壳在膛内的受力模型，如图2所示。其中p1为径向压力，p2和p3均为轴向压力;此外，弹壳受到膛壁的摩擦阻力设为FRK。

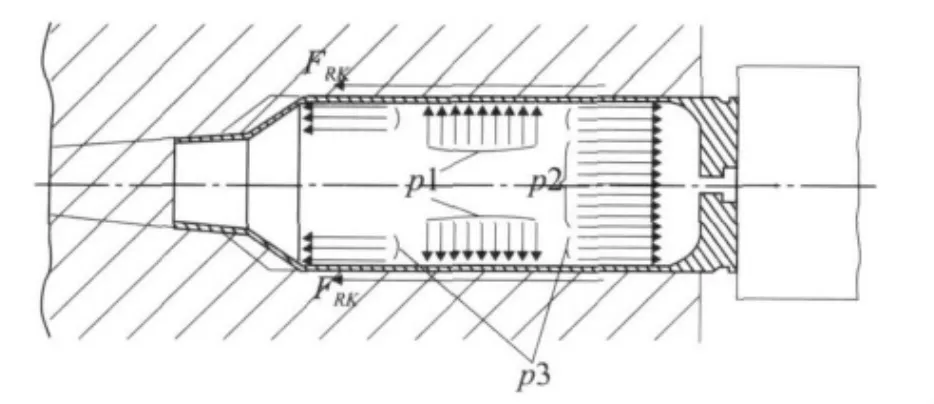
图2 发射时弹壳受力模型

由图2可知，在弹丸发射之初，由于膛内火药燃气的压力不高，故作用在弹壳上摩擦阻力FRK也不大。于是，在摩擦阻力FRK和轴向压力p2的共同作用下，弹壳将沿膛壁向后滑动并被拉伸，同时弹壳会推动枪机后坐。随着膛内火药燃气压力的快速升高，径向压力p1和轴向压力p2均随之增大，于是弹壳会急剧膨胀并紧紧贴于弹膛壁;加之火药燃气温度升高，因此弹壳和膛壁之间会形成金属和金属在高温高压作用下的紧密贴合，从而使摩擦阻力FRK急剧增大。此时，轴向压力p2和摩擦阻力FRK的合力在推动弹壳后坐的同时，也会使弹壳内产生很大的轴向拉伸应力。如果弹壳较长且膛压较高，则该拉伸应力就会很大，于是弹壳就可能被过度拉伸至材料极限而被拉断，即产生弹壳横向断裂故障。

另一方面，如果枪机后坐速度过大，使弹壳过快退出弹膛，以致其底部径向薄壁部分失去弹膛支撑，则弹壳底部可能会炸裂。此外，由于该运动枪机所用枪弹为有一定锥度的弹壳，如果该锥度过大，当弹壳向后移动时，在弹壳与弹膛壁间会出现较大间隙，此时火药燃气压力会迫使弹壳膨胀变形以填充该间隙，从而可能导致弹壳破裂。上述炸裂或破裂均属于弹壳纵向破裂故障。

综上所述，对于采用自由枪机的新型突击步枪来说，保证弹壳正常工作是十分重要的。弹壳破裂或过度变形都会严重影响该枪的可靠性，甚至会危及射手安全，因此在设计时必须对上述弹壳故障进行详细预测和分析［4］。

3.1 弹壳可以移动的条件

设弹壳及与其连接枪机的总质量为m，枪机在某瞬时的后坐速度为 v－，枪膛横断面积为S，膛内平均压力为 p（约等于膛底压力）。再设弹壳与膛壁间的摩擦阻力为FRK，枪机所受复进簧力为Ff，枪机所受摩擦阻力FR。根据自由枪机式自动武器的基本原理［5］可知，枪机运动微分方程为:

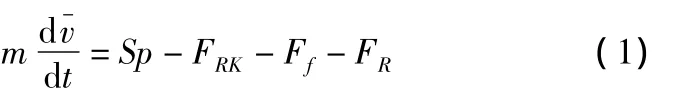
在枪弹发射过程中，Ff和FR的值比Sp和FRK的值要小很多，因此在分析时可忽略Ff和FR，这种不考虑Ff和FR的枪机后坐即称自由后坐。于是，枪机自由后坐运动微分方程为:

为保证弹壳能推动枪机自由后坐，首先弹壳必须可以移动，即满足Sp－FRK＞0，也即:

所述“回”型运动枪机的弹壳外形近似为圆筒形，故可设弹壳底部外径为d2，弹壳埋入弹膛的长度为l，其值近似为弹壳体部以上的长度。设弹壳与膛壁间摩擦系数为f，其范围为0.1～0.15。弹壳与膛壁间的正压力即为图2所示的径向压力p1，于是:

结合式（3），得:

上式可化为:

上式右端是弹壳可以移动的极限长度，它具有长度的量纲，故设其为llim，即令:

综上，可得弹壳可以移动的条件为:

式（8）表明，对于该运动枪机来说，为使弹壳可以顺利带动枪机组件后坐，弹壳埋入弹膛部分的长度l必须小于其可以移动的极限长度llim。

设弹壳壁厚为δ，所用材料弹性极限为σe，屈服极限为σb。设当弹壳内所产生的切向应力达到材料弹性极限时的压力为pe。忽略材料塑性变形强化，根据材料力学薄壁圆筒强度理论［6］，可得:

于是，弹壳和膛壁之间的正压力可表示为:

对于该运动枪机而言，当p=pm=151.3 MPa时，弹壳与膛壁间的摩擦阻力最大，弹壳最有可能无法移动。已知弹壳底部外径d2=8 mm，弹壳底部壁厚δ=0.84 mm，于是可得:

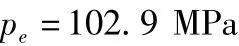
所以:

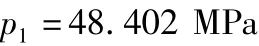
为尽可能满足极限条件，f取最大值0.15。将所有参数代入式（7），解得弹壳可以移动的极限长度为:

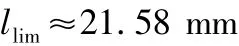
对于该运动枪机而言，其弹壳埋入弹膛的长度为:

与弹壳可以移动的极限长度llim相比，满足l＜llim。因此，基于上述分析可以预测:弹壳可以顺利移动，枪机组件与弹壳可以自由后坐。

3.2 弹壳横向断裂故障

基于上述分析，当弹壳埋入弹膛的长度l小于极限长度llim时，在膛底压力p2和摩擦阻力FRK的合力作用下，弹壳可以带动枪机组件顺利后坐。但是，p2和FRK的共同作用会使弹壳被拉伸，而当拉伸应力过大时，弹壳就有可能被拉断，即产生横向断裂。

如图3所示，取弹壳上任一横断面A来进行分析，设该横断面与弹膛末端的距离为x。设膛底压力p2作用在该横断面上的合力为Fp，打有剖面线部分的弹壳所受摩擦阻力为FRx，力Fp和FRx的共同作用可使横断面A产生拉伸变形，其中FRx越大，则横断面A的拉伸程度也越大。摩擦阻力FRx的值为:

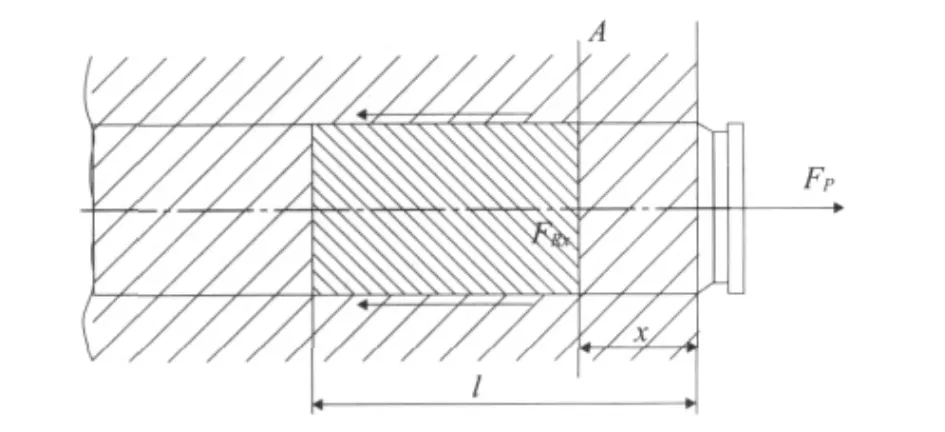
图3 弹壳拉伸作用力

由式（11）易知，FRx随x的增大而减小。由此可知，弹壳在膛底处横断面所受摩擦阻力最大，该最大值即为之前所述的FRK，即:

假设弹壳等壁厚，则最大变形将发生在x=0处，即弹膛末端处的弹壳横断面上。为保证弹壳不发生横向断裂故障，其所受摩擦阻力的最大值必须小于弹壳被拉断前能够承受的最大抗力，即满足:

代入式（9）、（10），有:

令plh为弹壳不被横向拉断时的极限膛压，则:

综上，可得不发生弹壳横向断裂故障的条件:

对于该运动枪机而言，将已知数据代入式（15），可得:

式中:为尽量满足极限条件，f取0.15。由内弹道分析结果可知，所述运动枪机最大膛压为 p=pm=151.3 MPa，故满足式（16）的条件。综合以上分析可知，本文所述运动枪机在射击时，其所用弹壳不会发生横向断裂故障。

3.3 弹壳纵向破裂故障

在弹壳可以移动以及不会发生横向断裂的情况下，弹壳仍有可能发生纵向破裂。具体来说，如果在发射时枪机组件后坐速度太大，以致枪机与弹壳向后移动的距离过大而超出了许可位移（如图4所示），弹壳薄壁部分就会失去弹膛壁的支撑。若此时膛压较高，则弹壳就可能过度膨胀变形而发生纵向破裂故障。

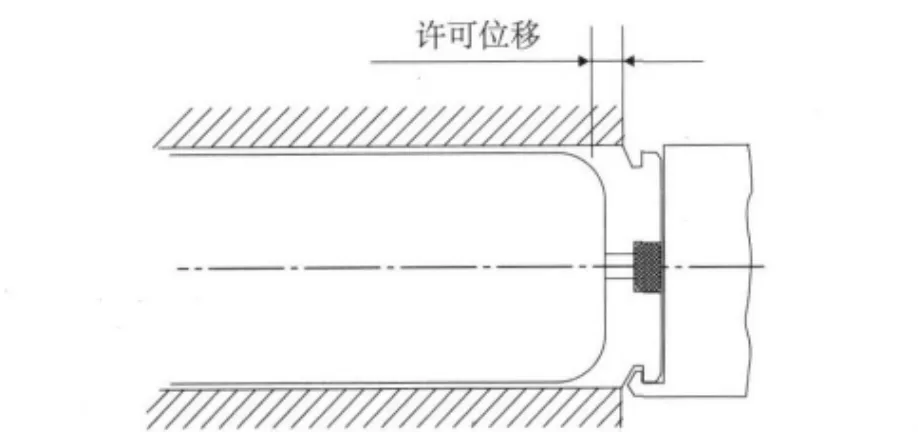
图4 普通底缘弹壳的许可位移

为保证弹壳在发射时不发生纵向破裂故障，必须满足的条件为:令plz为弹壳产生纵向破裂的极限膛压，则:

于是，可得不发生弹壳纵向破裂故障的条件:

对于该运动枪机而言，将已知数据代入式（18），可解得:

根据内弹道分析结果可知，所述运动枪机的最大膛压为 p=pm=151.3 MPa，看似并不满足式（19）中 p＜plz的条件。然而事实上，对该运动枪机而言，在最高膛压时弹壳并未失去弹膛的支撑，而当弹壳薄壁部分离开弹膛时，火药燃气压力已然不是最大膛压值。具体来说，根据所用弹壳结构可知，在膛压较高阶段弹壳允许后坐的位移为lk=1.5 mm，设对应的弹头行程为ld，于是根据质心运动守恒定律可得:

式中:m0为弹头质量，其值为2 g;m为枪机以及与其连接的弹壳的总质量，其值m=248.5 g。于是可以解得，弹壳薄壁部分外露时对应的弹头行程为:

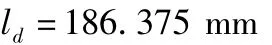
依据所述运动枪机内弹道计算结果可知，当弹头行程为186.375 mm时对应的膛压约为86.335 MPa，其值小于117.39 MPa。所以可以预测，该运动枪机在射击时，其所用弹壳不会发生纵向破裂故障。

4 结论

本文对突击步枪“回”型运动枪机在完成退壳动作时可能出现的故障（弹壳横向断裂、弹壳纵向破裂）进行预测分析。对于突击步枪“回”型运动枪机的两种故障，主要依据枪机自由后坐的运动特性，分析了发射时弹壳的受力情况，讨论了弹壳可以自由后坐运动的条件，并得出了弹壳不发生横向断裂和纵向破裂故障的条件。然后参照所述突击步枪内弹道计算结果，预测出在取定已知设计参数的条件下，所用弹壳不会发生横向断裂和纵向破裂故障。

［1］朱玉珍.突击步枪及其技术［J］.轻兵器，2002，（3）:10-12.

［2］ Chris Kent.Small Arms——The Main Battle Weapons of the World's Major Countries［M］.The Chinese Market Press.2009:235.

［3］赫雷，周克栋，骆家光.某自动武器弹性抛壳过程仿真分析［J］.弹道学报，2010，22（3）:35-38.

［4］甘高才.自动武器动力学［M］.北京:兵器工业出版社，1990.16-21.

［5］吴臣武.枪械发射过程中弹壳动态响应分析［D］.南京:南京理工大学硕士学位论文，2004:1-13.

［6］甘高才.自动武器动力学［M］.北京:兵器工业出版社，1990.16-21.

［7］翟越，魏雪英，计琳，等.薄壁圆筒在双剪统一强度理论下的统一解［J］.长安大学学报（建筑与环境科学版），2004，21（3）:1-3.