基于有限元的贴片机横梁结构优化设计

张长军，孙杰，于泷，张文识

（辽宁石油化工大学机械工程学院，辽宁抚顺 113001）

对贴片机设计来讲，横梁是设计的关键部件，其质量、强度、动力学特性以及抗震能力都影响着贴片机的贴装速度与精度。横梁有多种结构形式，这与贴片机的传动结构形式有关［1］。由于横梁所起的关键作用，仅仅依靠传统的经验设计和静力校核无法获得良好的动态品质，这就要求从动态特性的角度对横梁进行优化设计。贴片机工作时横梁承载了其复杂的载荷，基于有限元的模态分析可以确定结构的固有频率和振型，从而可以获知各种载荷作用下产生的实际振动响应。本文基于有限元模态分析，在求出横梁优化设计截面参数的基础上，对贴片机横梁进行优化设计。贴片机虚拟样机结构如图1所示。

图1 贴片机虚拟样机结构

1 ANSYS软件优化设计介绍

ANSYS提供了两类优化方法:零阶方法和一阶方法［2］。零阶方法属于直接法，它通过调整设计变量的数值，采用曲线拟合的方法去逼近状态变量和目标函数，可以有效的对大多数工程问题进行处理。一阶方法为间接法，是基于目标函数对设计变量的敏感程度的方法。在每次迭代中，根据计算梯度确定搜索方向。由于其每次迭代中都要产生一系列的子迭代，所以占用时间较多，但是有比较高的计算精度，适用于精确的优化分析。ANSYS软件提供了一系列的分析－评估－修正的循环过程，通过对初始设计进行分析，对分析结果进行评估，然后更改设计，并且这一循环重复进行直到完成优化设计。

2 优化设计理论基础

优化问题的数学模型是实际优化设计问题的数学抽象［3］。在明确设计变量、约束条件、目标函数之后，优化设计的问题就可以用一般数学形式表示。

求设计变量向量x=［x1，x2，…，xn］T使

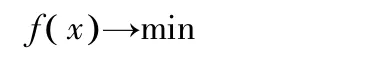
且满足约束条件:

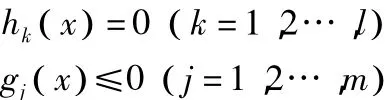
在ANSYS优化程序中，设计变量（design variables）为自变量，通过改变自变量的数值来实现结果的优化。每个设计变量通过上下限来确定其变化范围。一般可以定义60个设计变量，但最好不要超过10－20个设计变量，因为太多的设计变量，就很容易收敛于一个局部最小值［4］。

状态变量（state variables）是约束条件的数值。他们是设计变量的函数，是因变量。状态变量一般可以有上下限或者单方面限制，以确定其变化范围。一般可以定义不超过100个的状态变量。

目标函数（objective function）是设计要达到的尽量减小的目标值，是设计变量的函数。如果要尽量增大，那目标函数可以通过倒数或加负号确定。目标函数只设置一个。

3 参数化建模及分析

3.1 建模及模态分析

1）参数化建模

在ANSYS软件中对贴片机横梁进行原始设计，首先参数化建模，然后设置局部变量，设置参数

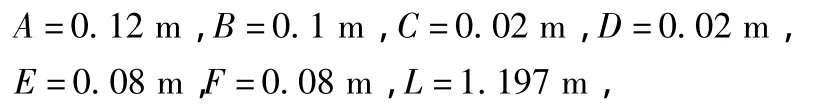
因此，横梁体积可表示为。

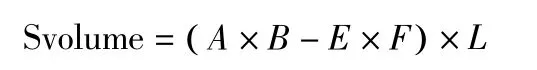
横梁横截面参数如图2所示。

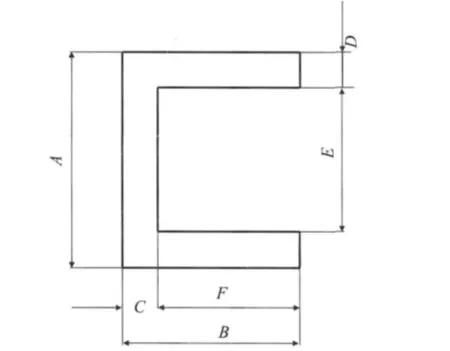
图2 横梁截面参数

2）定义单元类型和材料属性

设置单元属性为20solid95，solid95是三维20节点结构实体单元，由20个节点定义，每个节点有三个自由度，允许沿节点坐标系x，y，z方向的平动。

贴片机横梁材料选择45号钢，杨氏模量为:E=2.09e11 Pa，泊松比:u=0.269，密度为:7 850 kg/m2。

3）网格划分、加载及求解［5］。

利用MeshTool，激活 Smart Size，设定 smart size为3，采取自由划分网格方式，可以得到较好网格密度。

贴片机横梁加载的载荷类型包括DOF约束、集中载荷、惯性载荷、初始条件和边界条件。横梁底面的两端将与贴片机直线导轨接触，将受到滑动摩擦力和导轨的垂直向上的支撑力等外力，可以把这些外力载荷简化为横梁底端的两条断线［6］，在ANSYS中设置其自由度约束为ALL DOF=0。

约束条件设置完成以后，进行求解，求解完成后，可以查看原始设计横梁的16阶振型云图如图3所示

图3 原始设计横梁16阶振型云图

3.2 优化设计数学模型

1）确定优化设计变量

要完成贴片机横梁的优化设计，目的是在满足条件的情况下，尽量减小横梁的质量。由于选择材料的同质性，而质量和横梁体积有密切关系，所以本文要对横梁体积进行优化。要使体积最小，在长度一定的条件下，设计合理的横截面尺寸，应使横梁的横截面积最小。与横截面积相关的设计变量有参数A，B，C，D，根据直线导轨的安装尺寸和其他条件限制，对设计变量做如下的约束:

0.09 m ＜A＜0.13 m，0.07 m ＜B＜0.11 m

0.005 m ＜C＜0.03 m，0.02 m ＜D＜0.035 mm

具体定义设计变量命令为:

OPVAR，A，DV，0.1，0.13，0.000 3，

OPVAR，B，DV，0.07，0.11，0.000 4，

OPVAR，C，DV，0.01，0.03，0.000 2，

OPVAR，D，DV，0.02，0.035，0.000 15，

2）状态变量

根据横梁驱动机构的尺寸限制定义状态变量E，F，其中E=A－D，F=B－C。根据所选伺服电动机额定转速为2500 r/min，最高转速为3000 r/min，其工作频率为41.67 Hz，最高频率为50 Hz，所以整个贴片机的工作频率范围大约为050 Hz。为了避免发生有害共振，根据结构系统的频率设计的原则，对横梁的一阶固有频率FREQ1进行限制，以满足横梁的动态性能要求。状态变量的约束如下:

0.06 m ＜E，0.06 ＜F，120 Hz＜FREQ1

具体定义设计变量命令为:

OPVAR，E，SV，0.06，，0.000 8，

OPVAR，F，SV，0.06，，0.000 8，

OPVAR，FREQ1，SV，120，，1.2，

3）目标函数

本文所设计的目标函数为横梁的体积，在满足横梁条件下，使得横梁体积最小化，那么横梁质量就会相应减小，从而达到节约设计成本的目的。横梁的设计体积用Svolume表示，Svolume= （A×B－E×F） ×L。

具体定义目标函数命令如下:

OPVAR，SVOLUME，OBJ，，，6.703 2e －005

4 优化结果及分析

选择零阶优化方法，通过选定Sub－Problem，并用Opt Database－Save保存 OPT数据库，然后通过Run进行优化。经过十次迭代循环终止，第十次迭代结果也是最优解。贴片机横梁的全部优化步的优化数据如下所示:

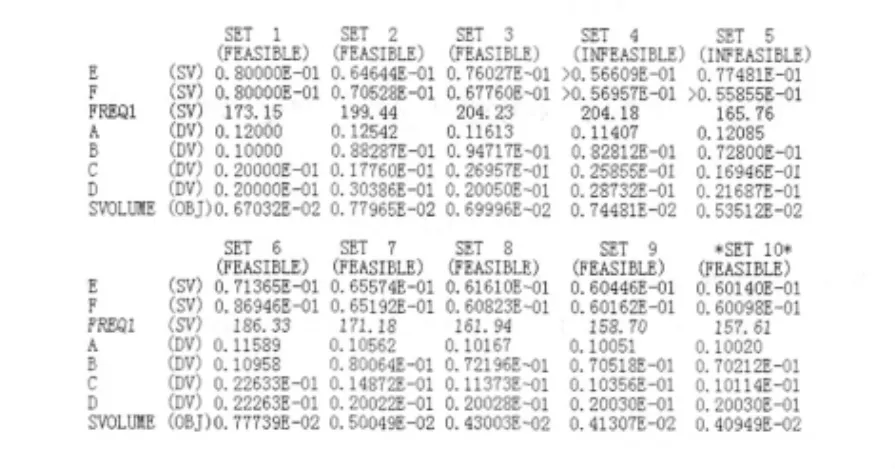
从优化结果可以看出，在保证较高的一阶频率的情况下，横梁的质量得到了很大的降低。具体迭代次数与横梁体积、一阶频率关系如图4所示。

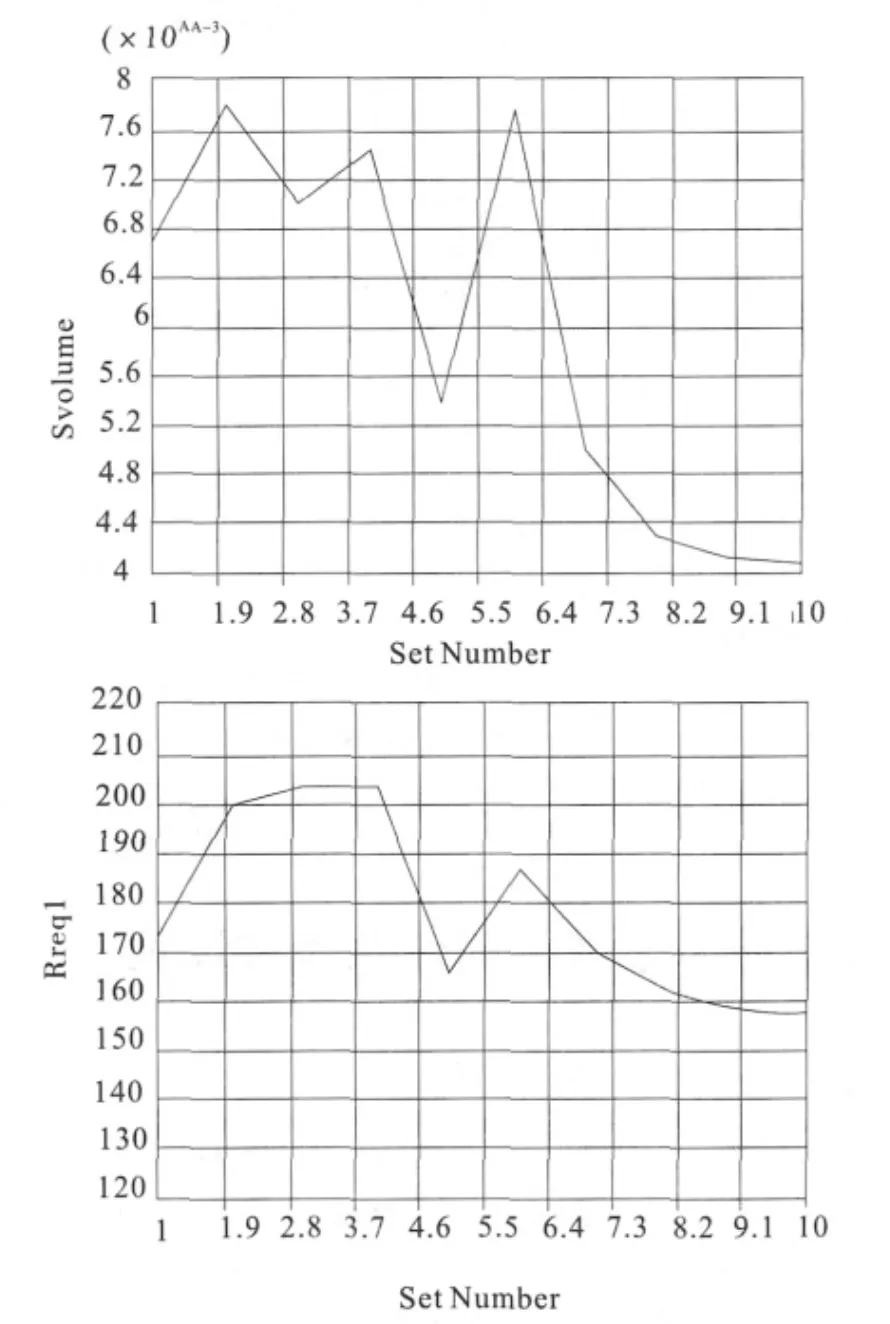
图4 体积、一阶频率与十次迭代关系图

现在以第十组横梁截面参数数据为基础，进行优化设计，并设计出两种优化方案，横梁优化前后结构对比如图5 所示［7］。

图5 横梁优化前后结构对比

运用ANSYS软件对两种优化设计方案进行模态分析，得出横梁前六阶频率、体积及质量与原始设计对比如表1所示。

从表中数据可以看出，在保证横梁较高的一阶频率的基础上，优化方案一横梁的体积比原始设计下降32.8%，优化方案二横梁的体积比原始设计下降了26.7%，那么横梁质量也得到相同程度的降低。

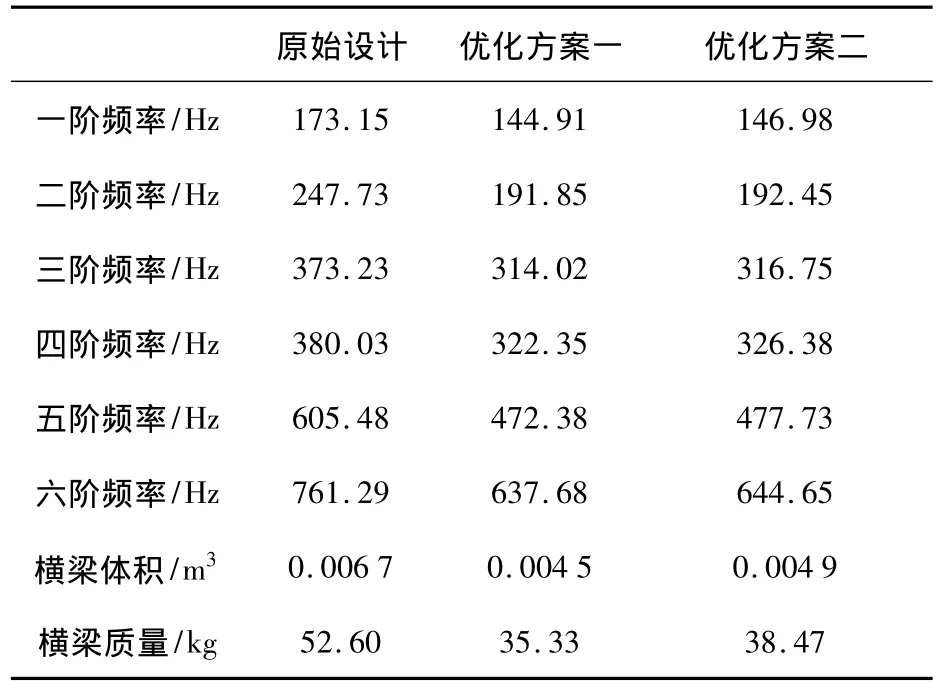
表1 原始设计方案与优化设计方案比较

5 结论

运用ANSYS软件，在对贴片机横梁进行模态分析的基础上，对横梁进行优化，得到了满足贴片机动态性能的横梁截面尺寸。在此基础上，对横梁进行优化方案设计，并对设计结果进行动态分析。经过比较，优化方案一、二都能较好的满足设计要求，并且使设计横梁质量显著降低。应用有限元优化设计方法，可以使贴片机横梁截面尺寸的确定更加合理和科学，对实际中贴片机横梁设计方案确定、优化设计、制造具有一定的指导意义。

［1］贾春艳.贴片机研究与结构设计［D］.黑龙江:哈尔滨工程大学，2008（5）:57-59.

［2］王国强，赵凯军，崔国华.机械优化设计［M］.北京:机械工业出版社，2009.166.

［3］孙靖民，梁迎春.机械优化设计［M］.4版.北京:机械工业出版社，2006.19-22.

［4］尚晓江，邱峰，等.ANSYS结构有限元高级分析方法与范例应用［M］.北京:中国水利水电出版社，2005.243-260.

［5］赵海峰，蒋迪.ANSYS 8.0工程结构实例分析［M］.北京:中国铁道出版社，2004.157-163.

［6］张昀.电子元件贴装设备精密高速运动控制系统研究与设计［D］.广州:广州工业大学，2006（5）:35-44.

［7］宋福民，肖永山.贴片机x-y运动横梁结构设计研究［J］.电子工业专用设备，2007，152（9）:12-15.