频差存在条件下时延估计性能及参数选取方法研究

李志刚，焦念君，赵丰文

（解放军69079部队，乌鲁木齐830013）

0 引 言

无源时差定位系统具有隐蔽性强和测向定位精度高的特点［1］，在军事上具有广泛的应用前景。而时延估计精度是一个非常重要的参数，它直接决定了系统的定位精度。在时差无源定位中，通常需要使用空间坐标不同的多部超外差接收机对信号进行同步接收并下变频至某一固定中频。在实际应用中，由于无法保证2台独立接收机的本振频率完全一致，从而导致2路接收信号之间几乎总是存在中频频差，如何处理中频偏差问题将在很大程度上影响时延估计的精度。

［2］～［5］对频差存在条件下的时延估计问题进行了研究。其中主要的解决方法分为以下2类：时延频差联合估计法［2］和频差补偿法［3－5］。时延频差联合估计法采用了时频域二维搜索的方式，估计精度较高，但运算量大，难以工程实现；频差补偿法首先计算2路信号之间频差，对其中一路信号进行频差补偿之后再进行时延估计，算法在时域频域皆为一维搜索，运算量大大减少，但精度也随之较低。

通过以上参考文献可以得知，频差的存在确实降低了时延估计的精度，但现有文献都没有对其进行深入的理论分析。本文创建了频差存在条件下的时延估计模型；然后利用二阶统计理论，推导并得出了频差存在条件下时延估计的均值是一个频差和时域相关长度乘积的辛格函数，从理论上澄清了频差对时延估计精度的影响；最后利用具体的信号进行了仿真验证，并提出了在频差存在条件下时延估计参数的选取原则，具有重要的理论意义和工程参考价值。

1 频差存在条件下的时延估计模型

在实际工程应用中，由于2个接收站相距较远，不可能使用同一本振对接收信号下变频，将导致2路信号存在微小频差。假设2个接收站R1和R2所接收的信号分别为x（t）和y（t）：

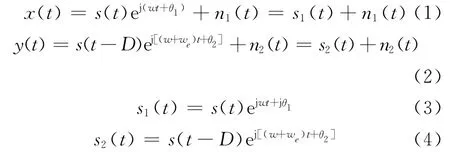
式中：s（t）为辐射源的基带信号；w为中频载波频率；we为由于接收机晶振频率差异带来的细微频差；θ1和θ2为2路信号的初相。

假设n1（t）和n2（t）为高斯白噪声，并且n1（t）、n2（t）和s（t）之间互不相关。D为信号到达2个接收站天线的相对时间延迟，也就是需要估计的时延参数。

2 频差对时延估计精度的影响分析

利用公式（1）和公式（2）所示的信号模型，可以通过寻找时域相关函数的最大值点得出2路信号的时延：

计算公式（6）所示的时域相关函数rxy（τ，we）的均值：

首先计算公式（6）中的第一项：

式中：rs（τ－D）为s（t）的统计自相关函数：

计算公式（6）中的后三项：

由公式（6）、（12）、（14）、（15）、（16）可得：

由公式（17）可得：

当频差we＝0时，也就是在不存在频差的条件下：

由公式（18）、（19）可得：

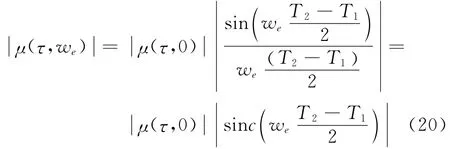
辛格函数的函数曲线如图1所示。

图1 辛格函数

由公式（20）可得出以下结论：

（2）时域相关函数的均值和初始相位无关，所以，初始相位不影响时延估计精度。

3 相关时间的选取与仿真分析

假设信号经过2部接收机正交下变频，第1部接收机的同相和正交分量分别为xI（n）和xQ（n），第2部接收机的同相和正交分量分别为yI（n）和yQ（n），如公式（22）～（25）所示：

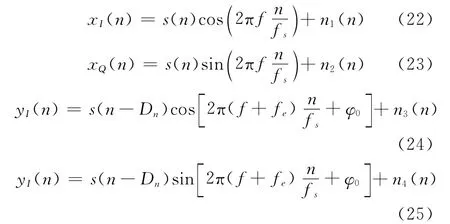
式中：s（n）为零均值高斯白噪声信号；n1（n）、n2（n）、n3（n）和n4（n）为零均值高斯白噪声；fe为频差；fs为采样频率；Dn为数字化后的时延：

假设f＝50 000Hz，fs＝10f，Dn＝10，在不同的频差fe与信噪比下，利用时域相关求最大值的方法计算2路信号之间的时延Dn，相关长度为N。

仿真1：时域相关长度N不变，变换频差fe和信噪比SNR。

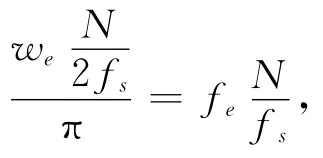
图2 相关长度恒定时，时延估计误差随频差的变化

当信噪比SNR＝－5dB，时延Dn的计算结果如图3所示。

图3 相关长度恒定时，时延估计误差随频差的变化

仿真2：频差fe不变，变换时域相关长度N和信噪比SNR。

图4 频差恒定时，时延估计误差随相关时间长度的的变化

4 结束语

参考文献

［1］Charles H K，Garter G C.The generalized correlatons methord for estimation of time delay［J］.IEEE Transactions on ASSP，1976，24（4）：320－327.

［2］Seymour Stein.Algorithms for ambiguity function processing［J］.IEEE Transactions on ASSP，1981，29（3）：588－599.

［3］束锋，吴乐南.一种实用的通信信号时差估计模型［J］.四川大学学报，2000，32（6）：92－95.

［4］王江，杨景曙.基于频差补偿的时延估计方法［J］.现代防御技术，2007，35（4）：100－103.

［5］王江，杨景曙.频差存在时广义相关时延估计方法研究［J］.信号处理，2008，24（1）：112－114.