考虑扭转效应的全直桩码头动力简化计算方法

何良德，张海荣，杨 洋，张志明，李新国

(1.河海大学港口海岸与近海工程学院，江苏南京 210098;2.江苏科技大学船舶与海洋工程学院，江苏镇江 212003;3.中交水运规划设计院有限公司，北京 100007)

港口工程桩基建筑物在地震作用时，桩、地震土、建筑物共同组成一个振动体系，它们在各自振动特性支配下相互作用、相互影响。桩基建筑物的上部结构计算模型主要有质点模型、刚片(体)模型、杆系+刚片模型和有限元模型。全直桩码头的纵、横向抗推刚度接近，特别是当码头宽度较大且长宽比大于2时，码头纵向抗推刚度及其抗扭刚度不容忽视［1］。基于基桩+刚性平台空间简化计算模型推导出的全直桩码头在水平静力荷载和温差作用下整体结构的简化计算方法是合理可行的，计算精度可以满足结构设计的需要，该计算方法为全直桩码头的三维动力简化分析提供了理论基础［1-2］。

如果桩基建筑物的结构布置不能满足均匀、规则、对称的要求，结构平面质量中心与刚度中心不重合，存在偏心的情况，则在水平地震作用下，结构除了平移振动外还会伴随扭转振动。大量震害调查表明，扭转将产生对结构不利的影响，加重结构的地震震害。现行JTS 146—2012《水运工程抗震设计规范》［3］是采用将纵、横向振型分别考虑并分别进行横排、纵排动力分析的一维方法，尚未提出考虑扭转效应的计算方法。

张志明［4］对桩基码头动力反应分析进行了研究，认为在水平动力荷载作用下高桩码头段可以简化为平面上的2个或3个自由度来计算。王守忠［5］对高桩(叉桩)码头单向振动时的平扭耦联振动和地震反应进行了研究，论述了高桩码头进行平扭耦联振动分析的必要性。李王红［6］采用ANSYS有限元分析软件对全直桩码头进行了结构温度分析、地震加速度反应谱分析以及弹性动力时程分析。

笔者结合全直桩码头整体结构的特点，建立了基桩+刚性平台空间简化计算模型，提出考虑扭转耦联效应的全直桩码头整体结构动力简化计算方法，并通过算例对所提算法的合理性进行验证。

1 全直桩结构动力计算方法

1.1 基桩+刚性平台计算模型

基于全直桩码头的整体模型试验、有限元模拟分析结果，其上部结构可作如下简化［1-2，7-8］:一般情况下，上部结构(现浇或装配整体式等梁板结构)水平向尺寸较大，在平面内抗弯刚度、抗剪刚度均远大于基桩的刚度。在水平力作用下，梁板结构水平面内变形很小，因此可将全直桩码头看作是由一个刚性平台通过桩顶连接下部各桩而组成的空间刚性平台桩系结构。

全直桩码头空间结构简化计算模型［1-2］如图1所示，一般情况下码头结构的横向、纵向、绕竖直向刚度较小，而其他方向上的刚度相对较大。振动主要发生在平面上的3个自由度方向，其余方向振动不明显，可以忽略。因此，在水平动力荷载作用下，全直桩码头结构段可以简化为平面上的2个或3个自由度来计算［4］。

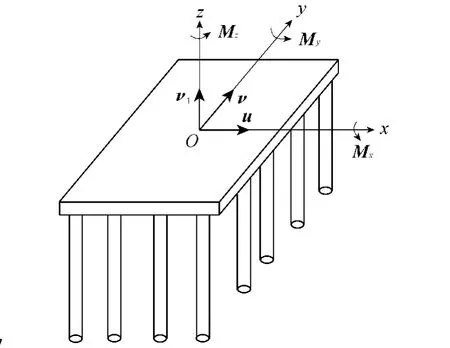
图1 全直桩码头空间简化计算模型Fig.1 Spatial simplified calculation model for all-vertical-piled wharf

1.2 平动扭转耦联振动方程

1.2.1 刚度矩阵

全直桩的局部坐标系可与整体坐标系取相同方向，因此第i根桩桩顶的局部坐标系位移δei与整体坐标系位移δi始终相同，它们与平台刚体(整体)位移δ0的关系可表示为

其中

式中:ux，uy，φz——第 i根桩桩顶的 x，y 方向位移及绕 z轴扭转角;u，v，γ——刚性平台的 x，y 方向位移及绕z轴的扭转角;Lδi——δ0与 δei间的转换矩阵;X，Y——第 i根桩桩顶的整体坐标。

在局部坐标系下，第i根桩桩顶力Fei与δei的关系式为

其中

式中:Hx，Hy，Mx，My——第 i根桩桩顶的 x，y 方向剪力，绕 x 轴、y 轴弯矩，kN，kN，kN·m，kN·m;Dei——第i根桩在局部坐标系中的单元刚度矩阵;ρ1——第i根桩的桩顶单位水平位移所需的水平力，kN/m;ρ2——第i根桩的桩顶单位水平位移所需的弯矩，kN。

将式(2)中的Fei转换为对平台的作用力Fi，则

其中

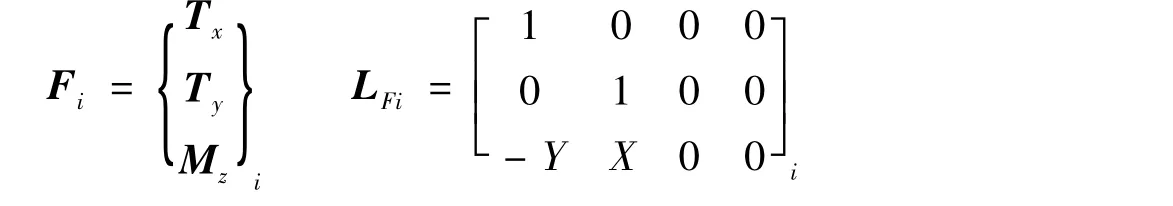
式中:Tx，Ty，Mz——第 i根桩桩顶对平台产生的 x，y 方向水平力及绕 z轴扭矩，kN，kN，kN·m;LFi——第 i根桩的Fei与Fi之间的转换矩阵。

所有桩顶对平台的作用力应与平台的外荷载平衡，有

其中

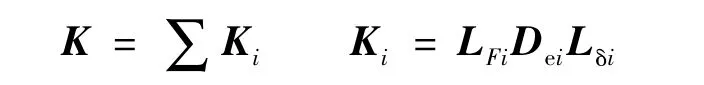
式中:Ki——第i根桩在整体坐标系中的刚度矩阵;K——平台整体刚度矩阵;R——平台的外荷载矩阵。

1.2.2 质量矩阵

通过桩单元质量矩阵，将桩顶对平台的质量贡献表示为

式中m1为桩顶质量系数，kg，其中梁板式高桩码头前附加动水质量可不予考虑［3］。

在刚性平台坐标系内，第i根桩桩顶单元质量矩阵为

上部结构的纵横梁、面板、堆载以及岸桥等装卸机械荷载等产生的质量矩阵，在局部坐标系内(与平台坐标系方向相同)质量矩阵可表示为对角矩阵:

式中:Mge——可分为体积分布、面分布、线分布、集中分布等类型刚体构件计算单元质量矩阵;Jz——平台刚体质量及其对z轴的转动惯量。

在刚性平台坐 系内，平台构件质量矩阵Mgi为

由桩顶、平台质量矩阵拼装组合成整体质量矩阵

1.2.3 固有振动方程

由于桩基不一定是对称布置，由式(9)组合的桩基整体质量矩阵不是对角矩阵。一般桩的折算质量在码头结构总质量中不到10%，为了简化振型分析可只取其中的对角线项。同时，选取平台的质量中心位置作为坐标系的零点，式(9)的M可简化为对角矩阵，最后得平台固有振动方程为

当桩基结构不对称时，由于刚度中心与平台质量中心不一致，导致水平振动与扭转振动耦联。可由式(10)的行列式得三次频率方程，解出3个自振频率ω，代入式(10)求得相应的振型位移向量。

1.3 反应谱法方法

ω，δ0求出之后，按照振型分解反应谱法［9-10］，第j质点在第k振型的地震荷载为

式中:Pjk——第j质点在第k振型的水平地震惯性力;Mjk——第j质点在第k振型的扭矩;mj——质点j的质量;γk——第k振型参与系数;φjk——第j质点在第k振型的位移值;βk——第k振型的动力放大系数，其值可由设计反应谱曲线确定;KH——地面加速度与重力加速度g的比值，称为水平地震系数，作为地震烈度的定量标志;Jj——质点j对转动轴的转动惯量;θjk——第k振型j质点绕转动轴的扭转角振型位移。

采用反应谱方法计算地震力，考虑了地面运动的强弱、场地土性质及结构动力特性对地震惯性力的影响，能够在相当程度上反映地震对结构的作用。求出等效地震荷载后，可计算结构内力。不同振型的位移、内力等反应量Si(i=1，2，3，…，n)的最大值一般不会同时达到，因此地震作用效应要考虑空间各振型的相互影响，采用完全二次方根法(CQC法)进行组合［10-12］。

2 算例分析

2.1 几何参数与计算参数

算例为一长45 m、宽15 m的全直桩码头结构段，面板厚0.5 m，码头面高程为5.4 m，设计码头前沿底高程为-5.53 m;每个横排布置4根钻孔灌注桩，直径d=800 mm，底高程为-45.0 m;下横梁、上横梁、纵梁的截面尺寸分别为1.3 m×1.2 m，0.7 m×1.4 m，0.7 m×1.4 m。横排间距为7 m，编号为排架1～7，各横排结构相同;纵排间距3 m，往陆侧向依次编号为1～6号。取1号桩桩顶为整体坐标系原点，横向以向岸侧为x正向，竖向向上为z正向，纵向为y向，满足右手坐标系规定。上部结构弹性模量E=3.0×1010Pa，泊松比ν=0.167，密度ρ=2500kg/m3。桩基E=3.25×1010Pa，ν=0.200，ρ=2500kg/m3。桩端采用弹性嵌固点法考虑，取嵌固深度5.0 m为假想完全固结。

算例工程所在区域的地震设防烈度为7度，根据工程具体的场地条件，场地类别为Ⅱ类场地。结构常阻尼比ξ=0.05，KH=0.1，综合影响系数C=0.4，采用文献［3］推荐的设计反应谱曲线进行抗震相应分析。

2.2 三维简化计算结果

取平台的质量中心位置(6.0，21.0，4.8)为相对坐标原点，平台刚度中心平面坐标为(9.02，21.02)。桩基按上下固接梁计算，ρ=，其中I=，l为桩长，单位为 m。m=+，其中 A=ρ为桩基11密度，kg/m3。由式(10)可得平台固有振动方程为

因此可求得各地震方向作用下各桩桩顶在各阶振型下的响应值，并按CQC法进行效应组合，其中y方向地震作用时，边角桩桩顶位移、内力组合值见表1。

表1 三维、二维简化方法计算的桩顶内力和位移(y方向地震作用)Table 1 Internal forces and displacements at pile top under y-direction seismic load obtained with 3D and 2D simplified methods

纵向均匀对称结构横向地震时，不产生扭转、纵向位移;纵向地震时，产生扭转，平台边角桩基有横向位移，其量值与横向地震时横向位移相当。平台边角桩基的合成水平位移、剪力和弯矩较大，危险状态发生在纵向地震时。

2.3 与水运规范法计算结果比较

文献［3］仅考虑纵、横向振型，固有振动方程可简化为二维方程:

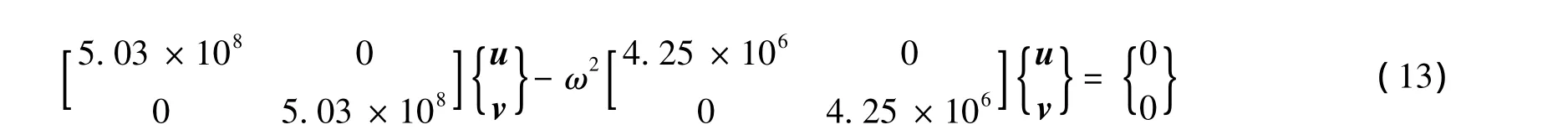
由表1可知，二维与三维谱分析组合结果相差较大，且随地震方向的变化规律不同。本例为全直桩码头，任何方向的抗推刚度相同，不考虑质量中心与刚度中心偏离时，相当于把全直桩码头看作平面内各向同性的结构。因此，二维谱分析组合的相应位移、内力合成值不随地震方向变化。二维与三维谱分析结果，在纵向地震(90°)附近两者差异最大，1号、25号等外侧边角桩顶位移、内力相差7%，4号、28号内侧边角桩顶位移、内力相差26%。

2.4 与有限元计算结果比较

全直桩码头有限元模型如图2所示，三维简化法计算的振型频率、周期与有限元计算值比较见表2。前3阶振型水平位移比较示意图如图3所示，第1阶、第3阶为平动与扭转耦联振型，第2阶为平动振型，这与全直桩码头整体模型试验研究规律一致［7］，三维简化法与有限元法的振型位移趋势基本一致。2种方法的桩顶内力、位移比较如图4所示。

图2 全直桩码头有限元模型Fig.2 Finite element model of all-vertical-piled wharf

表2 三维简化法与有限元法计算的振型频率、周期比较Table 2 Comparison of frequencies and periods of mode shapes between 3D simplified method and finite element method

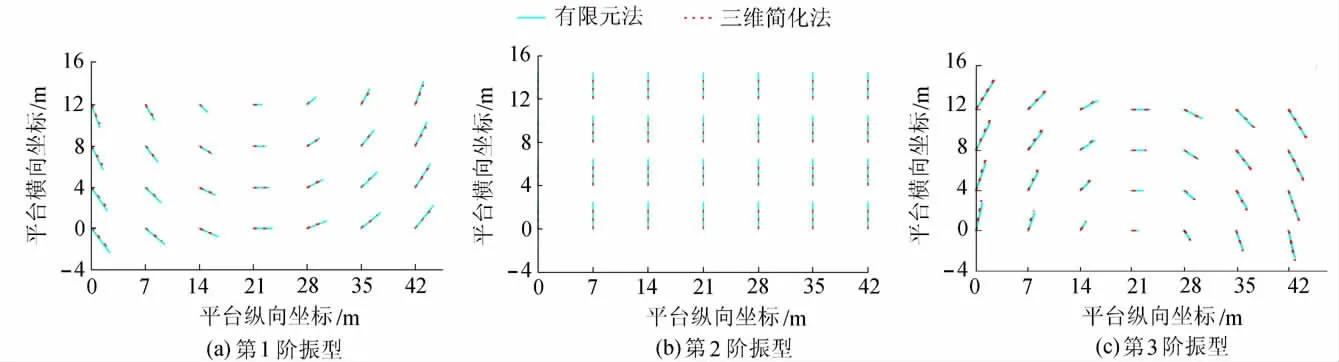
图3 三维简化法与有限元法的平台振型水平位移比较Fig.3 Comparison of horizontal displacements of platform for different vibration modes obtained with 3D simplified method and finite element method

刚性平台简化计算假设桩顶与平台完全固结，结构整体刚度大于实际刚度，因此简化计算的振型频率偏大。相对静力分析而言，动力简化分析时除结构刚度简化误差外，还会带来振型频率、动力放大系数、振型位移分布误差，因此动力简化分析的精度要低一些。

地震方向接近横向时，三维简化法与有限元计算结果吻合情况相对较好。地震夹角0°～30°时，三维简化方法的横向位移、横向剪力、纵轴弯矩、纵向位移、纵向剪力、横轴弯矩分别为有限元法的0.86倍、1.15倍、1.23倍、1.00～0.89倍、1.00～1.17倍、1.00～1.24倍。地震方向接近纵向时，简化法与有限元法计算结果相差要大些。地震夹角90°～120°时，横向剪力是1.16倍，纵轴弯矩是1.24倍，纵向剪力是1.17倍，横轴弯矩是1.23倍。

地震方向平行于结构平面刚度中心与质量中心的连线时，平台不产生扭转;地震方向垂直于刚度中心与质量中心的连线时，平台扭转效应最大。在水平地震作用下，平台扭转效应明显，设计计算时应考虑水平位移与扭转耦联。

图4 三维简化法与有限元法纵向地震(地震角90°)作用时桩顶位移、内力比较Fig.4 Comparison of displacements and internal forces at pile top under longitudinal seismic load with seismic angle of 90°obtained with 3D simplified method and finite element method

3 结 语

a.在水平地震作用下，可将全直桩码头简化为刚性平台下的桩系模型进行动力分析。算例表明，三维简化计算的三阶振型频率、周期、桩顶水平位移与有限元结果相当接近。二维与三维谱分析组合结果相差较大，且随地震方向的变化规律不同。

b.全直桩码头前三阶地震效应为主要影响。当刚度中心与质量中心不重合时，第1阶、第3阶为平动与扭转耦联振型，第2阶为平动振型。地震方向平行于刚度中心与质量中心的连线时，平台不产生扭转;地震方向垂直于刚度中心与质量中心的连线时，平台扭转效应最大。

c.质量和刚度分布明显不对称的高桩码头，应采用平动扭转耦联振型分解法计算地震作用及其效应。验算的水平地震方向应包括码头横向、纵向、平行于刚度中心与质量中心的连线方向及其垂直方向。

d.初步分析水平地震作用的扭转影响时，可采用振型分解反应谱法。由于全直桩码头前3阶振型的频率接近，应采用CQC法进行组合。

［1］张志明，何良德，李新国，等.在水平静力作用下全直桩码头结构整体简化计算方法［J］.中国港湾建设，2011(5):1-6.(ZHANG Zhiming，HE Liangde，LI Xinguo，et al.Simplified overall calculation method of all-vertical-piled wharf under lateral static loads［J］.China Harbour Engineering，2011(5):1-6.(in Chinese))

［2］何良德，张志明，庄宁.全直桩码头结构温度应力计算方法［J］.中国港湾建设，2010(增刊1):123-127.(HE Liangde，ZHANG Zhiming，ZHUANG Ning.Calculation methods of temperature stress in all-vertical-piled wharf［J］.China Harbour Engineering，2010(Sup1):123-127.(in Chinese))

［3］JTS 146—2012 水运工程抗震设计规范［S］.

［4］张志明.静水阻尼特性及桩基码头动力反应分析［D］.南京:河海大学，1990.

［5］王守忠.高桩码头平移扭转耦联振动分析与地震反应［J］.港口工程，1989(1):1-12.(WANG Shouzhong.Analysis on coupled translation and torsion vibration and seismic response of high-piled wharfs［J］.China Harbour Engineering，1989(1):1-12.(in Chinese))

［6］李王红.全直桩码头地震动力分析与桩基优化布置研究［D］.南京:河海大学，2008.

［7］王云球，朱秀峰，张祖贤.全直桩码头整体模型试验研究(大管桩码头结构物整体模型试验研究报告之二)［R］.南京:河海大学，1990.

［8］王墩，吕西林.平面不规则结构非弹性扭转地震反应研究进展［J］.地震工程与工程振动，2010，30(2):51-58.(WANG Dun，LUY Xilin.Progress in study on inelastic torsional seismic response of asymmetric buildings［J］.Journal of Earthquake Engineering and Engineering Vibration，2010，30(2):51-58.(in Chinese))

［9］李国豪.工程结构抗震动力学［M］.北京:科学技术出版社，1980.

［10］包世华.结构动力学［M］.武汉:武汉理工大学出版社，2005.

［11］GB 50011—2001建筑抗震设计规范［S］.

［12］徐培福，黄吉锋，韦承基.高层建筑结构在地震作用下的扭转振动效应［J］.建筑科学，2000，16(1):1-6.(XU Peifu，HUANG Jifeng，WEI Chengji.Response of torsional vibration of tall building structures induced by seismic action［J］.Building Science，2000，16(1):1-6.(in Chinese))