电力系统潮流计算的牛顿二阶法新解

康 丽，陈丽丹，刘 欣，张 尧

(1.东莞理工学院电子工程学院，广东东莞 523808;2.重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆 400044;3.华南理工大学广州学院，广东广州 510640)

牛顿二阶法［1］是包含二阶导数的牛顿-拉夫逊潮流算法，称为精确修正方程计算法，习惯上简称为牛顿二阶法。牛顿二阶法和快速解耦法是牛顿法在直角坐标和极坐标下发展最成功的2种算法，在20世纪八九十年代都得到了比较广泛的应用。牛顿二阶法需要计算二阶导数［2］，由于较多的数学推导，加上对三维矩阵的理解较抽象，因而求解较繁琐复杂，逊色于快速解耦法在电力系统潮流计算中的应用。但由于这2种算法都是一阶收敛，随着电力系统潮流计算的规模越来越大，这2种算法都无法独立进行大电力系统的潮流计算。

传统的牛顿-拉夫逊算法(简称牛顿法)的不足之处是对初值要求比较严格。电力工作者也将快速解耦法用于牛顿法的前几次迭代，即用于解决牛顿法的初值问题。实际上，牛顿二阶法较快速解耦法用于解决牛顿法的初值问题更具优点，因为它与牛顿法的连接非常方便，且编程简单［3-8］。

本文利用三维海森矩阵截面给出一个简单直观的牛顿二阶法中二阶导数项分解降维求解公式的推导方法，即当采用常规牛顿二阶法计算时，只需在计算牛顿法功率修正量的同时求解增量功率修正量，并将其加入到求解的功率或电压的不平衡量中。在此基础上进行的潮流程序设计，既可以选择牛顿二阶法不断修正其修正量，也可以选择通常的牛顿法。计算表明，在系统的规模较小、用于单独的潮流计算时，牛顿二阶法对初值的要求和收敛速度都有所改进。

1 牛顿二阶法的算法原理

众所周知，牛顿法就是保留非线性函数f(x)=0的泰勒级数展开式中的线性项，忽略Δx的二次项和高次项，利用逐次线性化的迭代求解方法求解［9-10］。牛顿二阶法则是保留其二阶导数项进行求解［1-2］。设多变量函数，有

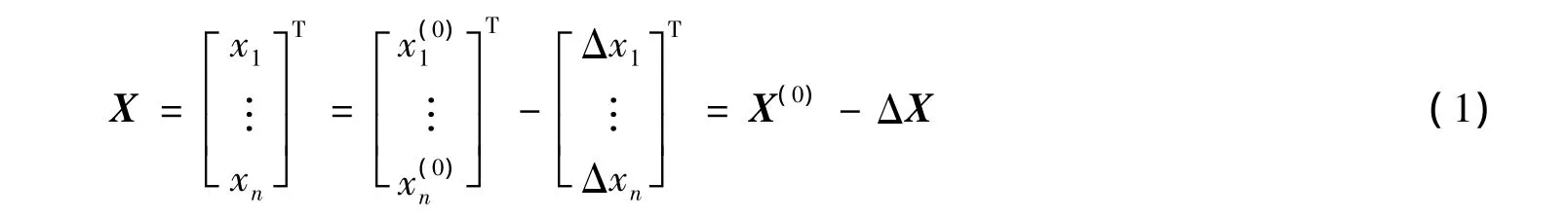
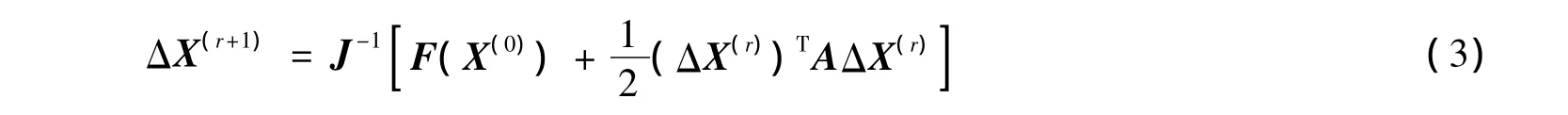
显然，A是三维矩阵，称之为海森矩阵。

若F(X)是二次函数，则其任何项的二阶导数均为常数，三阶及三阶以上的导数均为零。因而式(3)是其所求函数的泰勒级数展开式的精确表达式。

式(3)即为牛顿二阶法表达式。将牛顿二阶法与通常的牛顿法比较，可以看出牛顿法除了有函数初值为零的常数项外，还要加上一项含二阶导数的项。由于牛顿二阶法是对二次函数求二阶导数，显然从式(3)可知其二阶导数仍然是常数项。牛顿二阶法的关键在于对一阶和二阶导数项的求解。由矩阵相乘原理可知，三维矩阵与其对应的向量相乘，其结果是一个二维矩阵，二维矩阵再与其对应的向量相乘，结果是一维向量。因而式(3)中括号内是2个向量之和。即

式中向量F'(ΔX)的每一项元素是由三维矩阵A的对应截面(二维矩阵)与修正向量ΔX两次相乘的结果。

2 牛顿二阶法的求解过程

应用于电力系统潮流计算，设用直角坐标表示的二次方程式排列为

式中ΔP，ΔQ，ΔV分别为节点有功功率增量、无功功率增量和电压增量。其中，对PQ节点，其节点功率平衡方程表达式为

式中:e，f——节点电压的实部和虚部;G，B——节点导纳矩阵的实部和虚部;i——节点;j——与节点i直接相接的所有节点;s——PQ节点。

对PV节点，其电压平衡方程式也是二次方程式:

式(5)各项是以式(6)，(7)和(8)表示为直角坐标的节点功率和电压的平衡方程式。应用于牛顿二阶法求解式(3)的海森矩阵A的元素就是对式(5)，(6)和(7)求二阶导数的结果。由此可见，海森矩阵按照各自规律形成3个矩阵分块。由算法原理可知，三维矩阵与2个对应的向量相乘，其结果是1个向量，显然该向量的每个元素是相应的三维矩阵的截面，即对应的二维矩阵与2个向量相乘的结果。因此3个矩阵分块只要得3个二阶导数的通式(截面)，就可以求得F'(ΔX)的对应元素。

先选对应于有功方程(6)的二阶导数，即对应于海森矩阵A的一个横断面Api，即对应方程式ΔFi=ΔPi求得一阶导数Jpi，Jpi就是对应雅可比矩阵J的一个横向量，即

对式(9)求其二阶导数，可得Api是一个二维矩阵。

由于Api是对Jpi的每个元素再对所有的修正量求偏导数，则任一元素的全部偏导又组成2(n-1)阶的行向量，故Api是一个二维的2(n-1)阶矩阵，由一阶导数所得的雅可比矩阵元素的表达式知:

由式(10)可见，当j≠i时一阶偏导所得的公式只存在fi和ei的变量项，因而其二阶导数为对fi和ei的偏导等于常数，其余全部为零。当j=i时其二阶偏导分别是各变量的系数，故求得Api矩阵的各元素值为

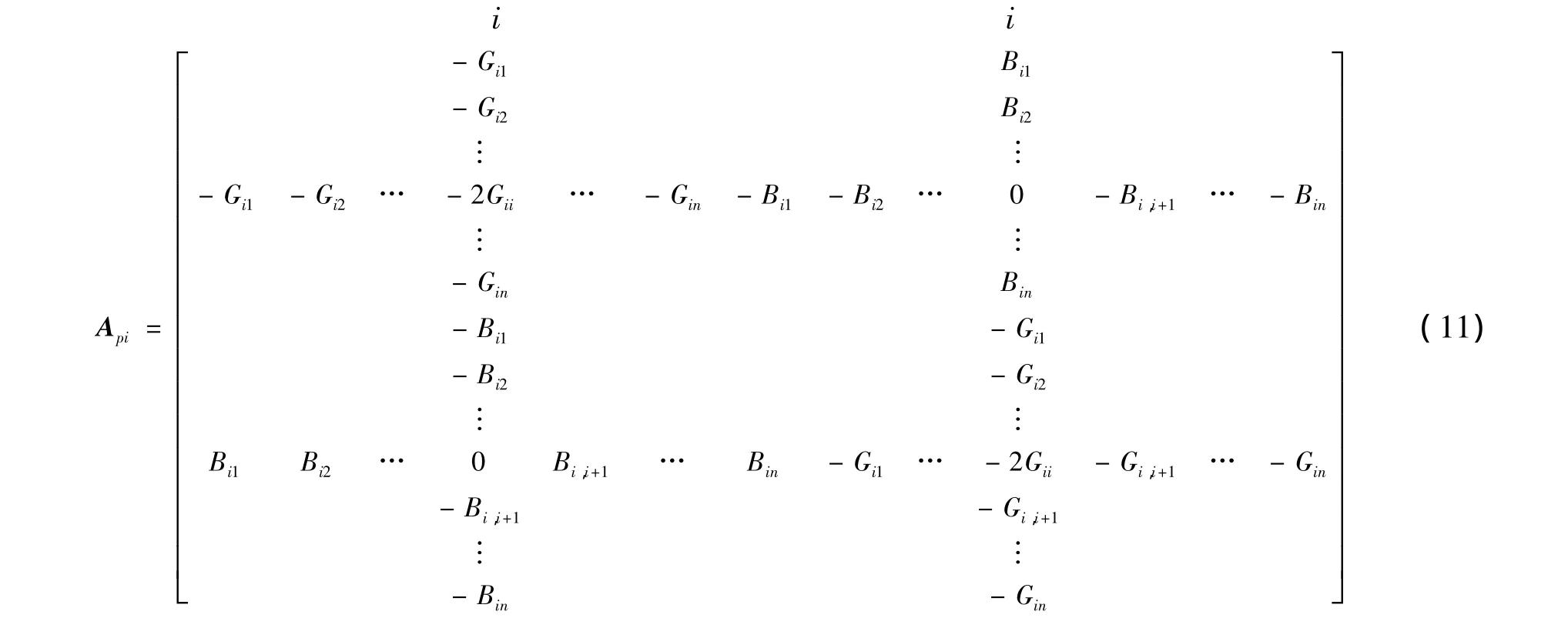
式(11)的特点是只有对应每个(n-1)中节点i的2行、2列为非零元素，其余的元素为零。将之应用于式(5)等号右边第2项的求解，Api左乘修正向量可得

对式(12)进行适当处理，可得

这样可以得到4个求和项为

则有

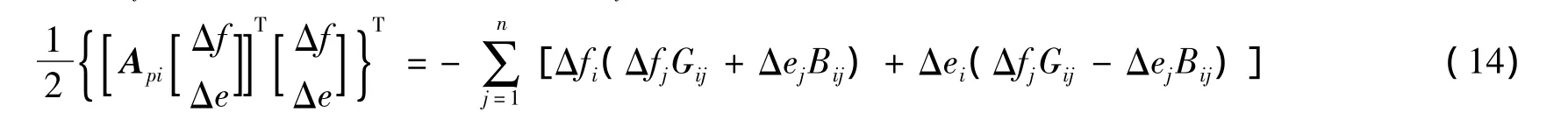
对比(14)与式(6)可知，将式(6)中含Pi，s的注入有功常数等于0，且e和f分别用Δe和Δf取代即为含二阶导数项的式(14)。

若节点无功功率方程的二阶导数海森矩阵A的一个横断面为Aqi，可求得Aqi矩阵，即其非零元素为两行两列:

同理可得

将式(16)与式(7)比较可知，将式(7)中含Qi，s等于0，且e和f分别用Δe和Δf取代即为含二阶导数项的式(16)。

对于PV节点电压平衡方程式(8)，显然，将式中的(Vi，s)2=0，再将fi和ei改成Δfi和Δei即得所求结果。

3 牛顿二阶法的计算

编制程序利用牛顿二阶法对标准的中国电力科学研究院24节点系统和新英格兰30节点系统等进行计算，其结果与牛顿法计算结果相同，表明其对初值的要求和收敛速度都有改进。

由于牛顿二阶法的J是按初值求得的，可能离真值较远，偏差较大。计算中若其取值始终不变，则可能会造成迭代次数过多甚至不收敛。因此在实际计算时，迭代3～5次后，重新计算J，其效果更佳。

牛顿二阶法是一阶收敛，因而对大规模电力系统的潮流计算不一定具有计算速度快的优点。但是由于牛顿二阶法与牛顿法的连接方便简单，因而以其前几次迭代的结果作为牛顿法的初值，以改变牛顿法对初值的苛求是有优势的。

4 结 论

将牛顿二阶法三维海森矩阵取其二维的截面，按照有功、无功和电压平衡方程式分割进行推导，只需在牛顿法的常数项再增加1个二阶导数项，而在原常数项的功率或电压平衡修正方程式中将常数项取零，变量以修正量取代即可求得该二阶导数的推导公式。如考虑交直流混合系统的潮流计算［11-13］，还需将文中列出的公式进一步演算。总之，该算法编程简单，易于与牛顿法连接。

［1］宋文南.电力系统潮流计算［M］.天津:天津大学出版社，1991.

［2］RAO PS.A exact load flow method including second order teams in rectangular coordinates［J］.IEEE Trans，1982:PAS-101.

［3］鞠平.电力系统建模［M］.北京:机械工业出版社，2011.

［4］江伟，王成山.电力系统输电能力研究中PV曲线的求取［J］.电力系统自动化，2001，25(2):9-12(JIANG Wei，WANG Chengshan.Solution of PV curve of the transmission capacity in electrical power system［J］.Automation of Electric Power Systems，2001，25(2):9-12.(in Chinese))

［5］宗秀红，张尧，武志刚，等.最临近功率极限点的概率计算［J］.华南理工大学学报:自然科学版，2006，34(10):89-93.(ZONG Xiuhong，ZHANG Yao，WU Zhigang，et al.Probabilistic calculation of the nearest power critical point［J］.Journal of South China University of Technology:Natural Science Edition，2006，34(10):89-93.(in Chinese))

［6］胡金磊，张尧，郭力，等.多运行方式下发电机变量的概率特性计算［J］.电力系统自动化，2007，31(11):39-43(HU Jinlei，ZHANG Yao，GUO Li，et al.Probabilistic characteristic calculation of generator variables under multi-operating conditions［J］.Automation of Electrical Power System，2007，31(11):39-43.(in Chinese))

［7］侯冠基，张尧，周二专，等.一种基于开源软件的新型电力系统网格计算平台［J］.电力系统自动化，2009，33(1):56-60.(HOU Guanji，ZHANG Yao，ZHOU Michael，et al.A new power system grid computing platform based on internet open sources software［J］.Automation of Electrical Power System，2009，33(1):56-60.(in Chinese))

［8］HUANG Qiuhua，ZHOU Mike，ZHANG Yao，et al.Exploiting cloud computing for power system analysis［C］//2010 International Conference on Power System Technology.Hangzhou:IEE Power ＆ Energy Sociery，2010:423-428.

［9］陈珩.电力系统分析［M］.北京:高等教育出版社，1980.

［10］王锡凡，周孝信.电力系统计算［M］.北京:水利电力出版社，1978.

［11］叶芳，卫志农，孙国强.含VSC-MTDC的交直流混合系统的改进潮流算法［J］.河海大学学报:自然科学版，2011，39(3):338-343.(YE Fang，WEI Zhinong，SUN Guoqiang.Modified power flow algorithm for hybrid AC-DCsystems equipped with VSCMTDC［J］.Journal of Hohai University:Natural Sciences，2011，39(3):338-343.(in Chinese))

［12］张孝，鞠平，陈谦，等.考虑频率特性的负荷模型研究及应用［J］.河海大学学报:自然科学版，2010，38(3):353-358.(ZHANG Xiao，JU Ping，CHEN Qian，et al.Study and application of load models considering frequency characteristics［J］.Journal of Hohai University:Natural Sciences，2010，38(3):353-358.(in Chinese))

［13］郑超，盛灿辉.含VSC-HVDC的交直流混合系统潮流统一迭代求解算法［J］.中国电力，2007，40(7):65-69.(ZHENG Chao，SHENG Canhui.Uniform iterative power flow algorithm for systems equipped with VSC-HVDCs［J］.Electric Power，2007，40(7):65-69.(in Chinese))