Mathematica对“通信电子线路”教学的促进作用

陈惠滨，黄艳洋，陈建容

(集美大学信息工程学院，厦门福建361021)

0 引言

“通信电子线路”是电子信息类专业的核心课程，该课程中除了高频小信号放大电路之外，主要涉及到电子元器件非线性工作过程。元器件的非线性工作过程一般采用复杂的数学模型描述。因此，如何把电路的工作过程，抽象成数学模型描述是学生必须掌握的能力。基于数学模型进行理论分析和求解，通常采用手工推导演算的方法，不仅费时费力，而且容易产生错误。为了克服以上不足，笔者在教学过程中引入了Mathematica辅助分析方法。

Mathematica软件是美国Wolfram Research公司开发的数学分析软件，具有数值计算、符号计算和图像处理等强大功能，使用非常方便［1-2]。它集成丰富的内部函数，用户通过输入简单的命令即可快速地进行方程求解、微分、积分运算和解微分方程等。Mathematica软件和Matlab相比，其功能毫不逊色，在科研和教学中有着广泛应用。笔者在“通信电子线路”教学中理论分析过程引入Mathematica软件，不仅可以防止复杂手工推导演算出现错误，还有助于加深学生对电子线路工作原理的理解。本文通过对波形振荡电路中几个具体问题的Mathematica解决方法，来说明该软件在“通信电子线路”教学中所起的作用。

1 Mathematica在振荡电路中应用

利用正反馈原理构成的反馈振荡电路是目前应用最广的一类振荡器。正反馈振荡电路是一个由主网络和反馈网络构成的闭合回路。要保证该闭合回路接通电源后从无到有建立起振荡波形，环路增益的复频域函数T(jω)必须满足起振条件、平衡条件和稳定条件［3-4]。其中，平衡条件是求解振荡频率的关键步骤，起振条件是设计电路元件参数的重要依据，稳定条件能确定选频网络。

RC电路构建的正弦波振荡电路，具有电路简单，经济方便等优点，但选频作用较差，一般用于频率较低、稳定性要求不高的场合。其中，以RC串并联选频网络构建的文氏振荡电路最为典型，文献［3] 对于该部分电路环路增益函数T(jω)的推导过程没有详细展开。学生对于该电路的起振条件、平衡条件和稳定条件无法深刻理解。我们在教学过程中结合文献［4] 的分析方法讲解，可以弥补文献［3] 对该部分理论分析的不足。

RC移相式振荡器是产生正弦波的另外一种重要方法，它是利用三阶以上RC电路可产生±180°相位差，构建正反馈电路，产生正弦波。文献［3] 对该部分电路的介绍较为简略，文献［4] 未涉及该部分内容。为了弥补上述文献对该问题讨论的不足，本文探讨了RC移相式振荡器的起振条件和平衡条件。由于RC高通电路与负反馈放大器构成的环路增益的相位变化与RC高通电路相位变化相同，呈下降趋势，相位满足稳定条件，因此对于相位稳定条件不必过多讨论。

2 RC移相式振荡电路

RC移相式振荡器如图1所示。图中的R1、Rf及运算放大器构成反相放大器，即输出电压VO和输入电压Vi反相，其等效输入阻抗为R1。由C1、R2、C2、R3、C3和R1构成三阶高通网络为反馈电路，最多可以产生270°相移。在某一频率点的相移为180°。此时VO经移相网络，加之运放输入端满足虚地条件，在R1端便形成正反馈。

在图1中，反馈网络输出端与放大器输入端直接相连。因此，放大器输入端输入阻抗是反馈网路的负载。将RC移相式振荡器闭合回路从图1反馈电路的×处断开，且保留V产生，可以得到等效的图2电路，其中反馈网路输出端负载等效为放大器输入阻抗Ri=R1。

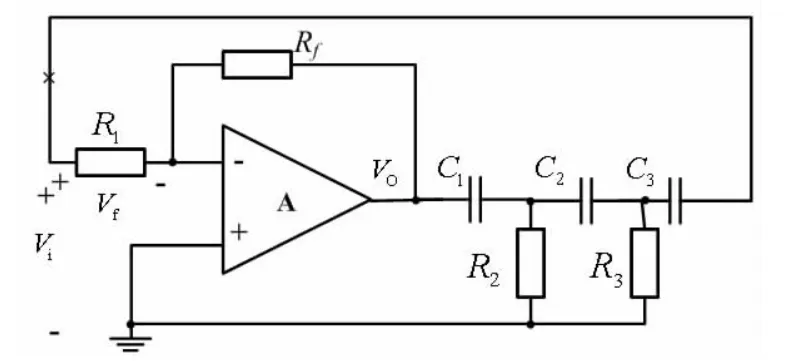
图1 RC移相式振荡器

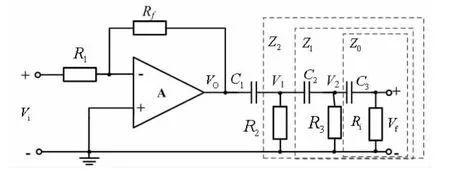
图2 移相式振荡器等效电路

根据环路增益T(jω)的定义，有

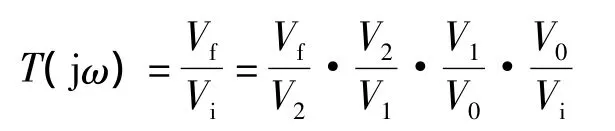
令图2中的Z0=1/(jωC1)+Ri，Z1=1/(jωC2)+R3//Z0，现设R1=R2=R3=R，且C1=C2=C3=C，则T(jω)可用以下Mathematica程序来描述:

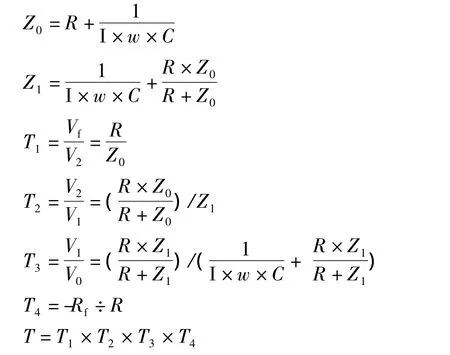
Simplify［T]

程序中的Mathematica复数符号用I表示，变量T代表T(jω)。

通过热键“shift+enter”执行程序，可以得到化简后变量T的表达式:

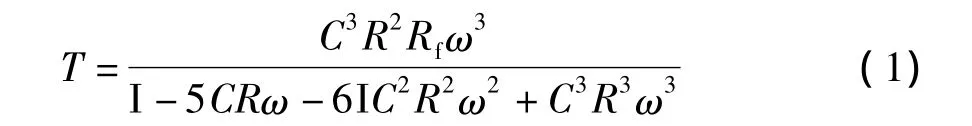
即环路增益

如要满足平衡条件，应令上式的虚部为0，即有j(1－6C2R2ω2)=0，解得产生正弦波角频率为ωosc电路要起振，上电至波形稳定这段时间要满足起振条件:

由此，可求得Rf/R＞29。选择Rf为负温度系数热敏电阻，随着Rf上消耗功率增加，Rf值减小，直到|T(jωosc)|=1，振荡器最终进入平衡状态，且满足幅值稳定条件:T(jωosc)/V＜0。

3 改进型RC移相式振荡电路

对图1所示的RC移相式振荡器进行改进后如图3所示。同理，由C1、R2、C2、R3和C3构成的反馈网络在某一频率点时，相移满足180°。此时VO经移相网络，在C3端产生的反馈电压Vf与Vi同相，形成正反馈。图3电路可以等效为图4电路，其中反馈网路输出端负载等效为放大器输入阻抗Zi=1/(jωC3)。

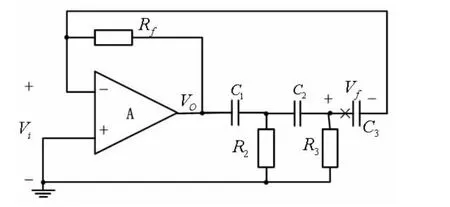
图3 改进型RC移相式振荡器

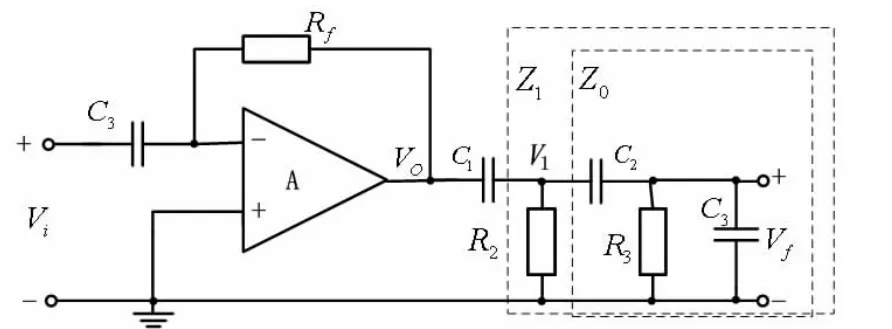
图4 改进型RC移相式振荡器等效电路

根据定义，其环路增益为

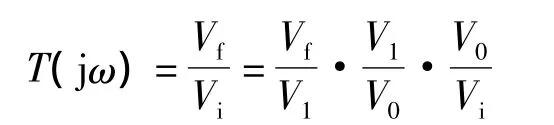
令Z0=1/(jωC2)+［1/(jωC3)] //R3，假设R1=R2=R3=R，且C1=C2=C3=C，可以用以下Mathematica程序描述T(jω)。

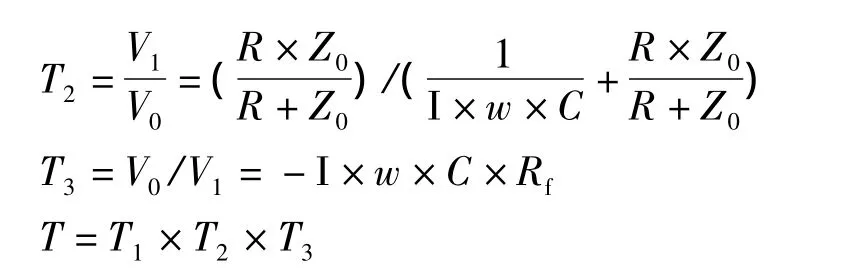
Simplify［T]

通过热键“shift+enter”执行程序，可以得到变量T表达式:

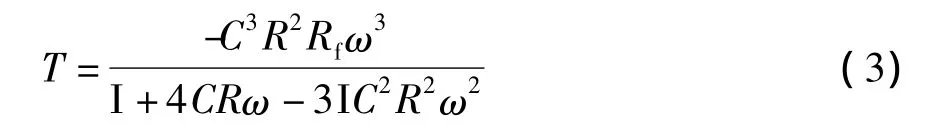
即环路增益:

令T(jω)表达式的虚部为0，满足平衡条件，即j(1－3C2R2ω2)=0，此时产生正弦波角频率为ωose电路要起振，上电至波形稳定这段时间要满足起振条件:

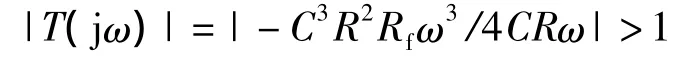
由此可求得Rf/R＞12。选择Rf为负温度系数热敏电阻。一旦出现|T(jωosc)|=1，振荡器进入平衡状态，且满足幅值稳定条件:T(jωosc)/V＜0。

4 结语

本文针对“通信电子线路”课程特点，以RC移相式振荡电路为例，利用数学分析软件Mathematica求环路增益表达式，对RC移相式振荡电路的起振条件、平衡条件及稳定条件进行分析。这些分析可以作为文献［3] 和［4] 中RC移相式振荡电路工作原理推导的有效补充，以弥补对此部分内容介绍过于简略的不足。将该部分教学过程中的盲点在课堂上展开深入探讨，以从理论层面上进一步加深学生对于振荡电路工作原理的理解。

［1] 唐，邓建松，彭冉冉.Mathematica使用指南［M] .北京:科学出版社，2002.

［2] 路洪艳，从守民，刘保通，等.Mathematica在大学物理教学中的应用［J] .淮北:淮北煤炭师范学院学报(自然科学版)，2010，4:020.

［3] 谢嘉奎，宜月清.电子线路:非线性部分(第四版)［M] .北京:高等教育出版社，1988.

［4] 童诗白，华成英.模拟电子技术基础(第四版)［M] .北京:高等教育出版社，2001.