“电力系统分析”中的同步发电机教学

黄 媛，刘天琪，李华强，邱晓燕

(四川大学电气信息学院，四川省智能电网重点实验室，四川成都610065)

同步发电机是电力系统中最重要、最复杂的动态元件之一，其模型及动态特性的分析是短路和稳定分析的基础，它是“电力系统分析”课程教学中的一个重点。本文对同步发电机模型的教学进行研究，以物理背景为依据，探索同步发电机的理论模型与工程应用模型相结合的教学思路［1-2]。

同步发电机模型在“电力系统分析”课程的稳态教学中是用最简单的电压源或电流源来表示，它同“电路原理”课程中的电源模型是一致的。发电机的电势和电抗通常由发电机的铭牌参数求取，然后将同步发电机模型与其它元件模型构成电力系统的数学模型，这是电力系统稳态分析的基础。随着短路和稳定教学的深入，需要更多地考虑同步发电机内部转子和定子在故障等情况下的相互关系，因此推导出用同步发电机的空载电势、暂态电势和次暂态电势等表达发电机端电压和电流之间的数学表达式。这部分内容包含大量的电、磁的相互转换和推导，一直是教学中的难点。本文在教学中，注重物理模型与数学模型的对应，简化推导过程，并通过实验课程，比较不同模型的仿真结果，强化感性认识。其基本教学思路如图1所示。

1 同步发电机模型

现代大容量的同步发电机较多采用旋转磁极式结构，按转子结构不同，通常分为凸极机和隐极机。一般汽轮发电机为隐极机，水轮发电机为凸极机［3]。为了描述发电机的模型，从图2所示较为复杂的有阻尼绕组凸极机同步发电机入手，分析其物理关系，简化模型。在该模型中考虑了定子a、b、c三相、转子d轴(直轴)的励磁绕组f和阻尼绕组D以及q轴(交轴)的阻尼绕组Q和g。

同步发电机的原始方程可以用相应的电压方程和磁链方程表示。在该方程中，由于自感系数和互感系数是随转子角周期性变化的，通常难以得到，因此采用派克变换将其转换为同步电机的基本方程。派克变换实际上是一个坐标变换［4]，它将定子的a、b、c三相的电流投影到随着转子旋转的d轴、q轴与垂直于dq平面的0轴上去，这组等效的电流产生的磁势相对转子是静止的，因此它遇到的磁路磁阻恒定不变，相应的电感系数也就变为常数了。

对同步发电机的基本方程可以通过恰当选择定子侧和转子侧各电磁量的基准值使其标幺值表示的互感系数可逆，并使磁链方程的系数矩阵也可直接用电感的标幺值表示。考虑到定子绕组中的0轴分量电流在空间产生的磁场为零，在方程中可以不考虑。因此用标幺值表示的同步发电机的基本方程如下式所示。

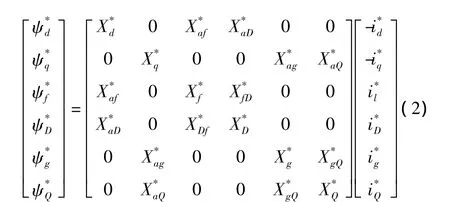
式中，v为各绕组端电压，i为各绕组电流:ψ为各绕组的总磁链=dψ/dt为磁链对时间的导数，R为定子和转子每相绕组电阻，X为定子绕组和转子绕组的自感电抗和互感电抗。

2 同步发电机实用模型的推导

以下讨论均基于标幺值系统，故省去了标准值上标“*”。式(1)和式(2)中用到同步电机原始参数通常很难求得，因此在工程上希望进行适当的转换，用电机参数进行描述。文献［5] 分别考虑了两种假设。第一种假设为:假定d轴方向各个绕组d、f、D之间和q轴方向各个绕组q、g、Q之间都只有同时匝链三个绕组的公共互磁通，而不存在局部互磁通;第二种假设在一定程度上考虑了各个绕组之间存在局部互磁通的可能性。本文采用第二种假设的推导，即有

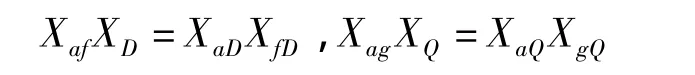
根据通常的电机参数定义，可导出如下的电机参数(等式左侧)同原始参数(等式右侧)的关系:

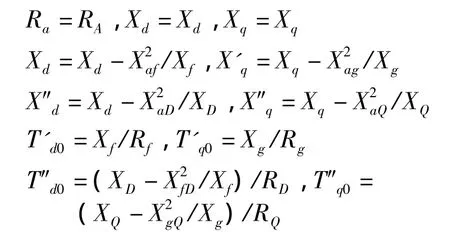
其中，Ra为定子绕组的电阻，Xd、Xq为交、直轴同步电抗，X'd、X'q为交、直轴暂态电抗，X″d、X″q为交、直轴次暂态电抗，T'd0、T'q0、T″d0、T″q0分别为交、直轴暂态和次暂态时间常数。

在电力系统分析计算中的状态变量通常是以等效电势表达的，而同步发电机的基本方程中的状态变量为磁链，因此可将磁链用电势进行相应表达。与转子各绕组磁链成正比的同步发电机的空载电势eq1、eq2、ed1、ed2、暂态电势e'd、e'q和次暂态电势e″d、e″q的定义如下:

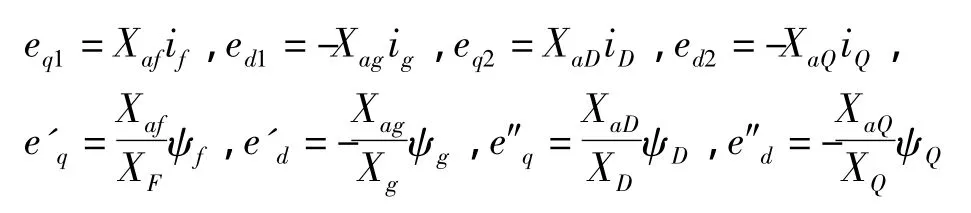
因此可得同步发电机转子绕组上的电压方程。现令Efq=(Xaf/Rf)uf，则可得

f绕组的电压方程:

D绕组的电压方程:

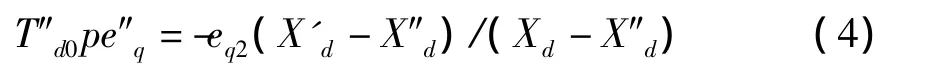
g绕组的电压方程:

Q绕组的电压方程:

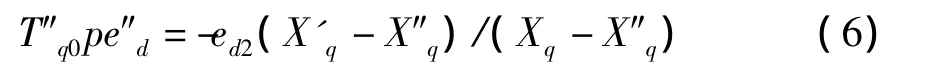
定子绕组的电压方程为

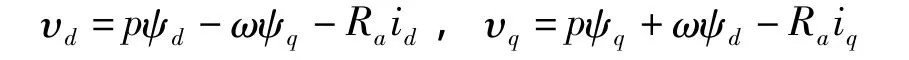
定子绕组的磁链方程为

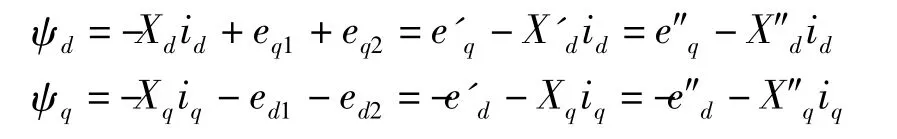
它可用空载电势、次暂态电势、暂态电势表示。

当同步发电机的转子视作刚体时，转子的运动方程为

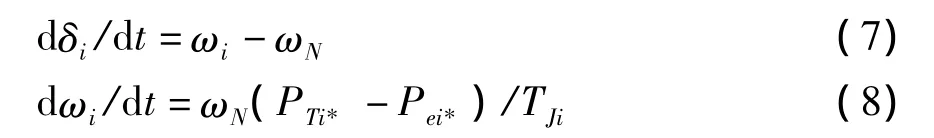
式中各变量和参数的含义见文献［4] 。

3 不同阶数的电机模型

1)同步发电机的6阶模型

通常所说的发电机的6阶模型由式(3)～(8)组成。该模型描述实心转子的汽轮机，它计及了发电机转子d轴的励磁绕组f绕组、阻尼绕组D以及q轴上的Q、g绕组的暂态和次暂态过程。其中磁链变量ψf、ψD、ψQ和ψg分别用电势e'd、e'g、e″d和e″g表示推导得出。

2)同步发电机的5阶模型

当发电机为凸极机时，不计q轴上g绕组的暂态过程，即ig=0，只考虑f、D、Q绕组时，可将6阶模型简化为5阶模型。它用e'g、e'd、e″g取代磁链变量ψf、ψD、ψQ推导得出。

3)同步发电机的4阶模型

当忽略q轴上g、Q绕组以及d轴的D绕组的暂态过程(即不计及阻尼作用)时，即ig=iQ=iD=0，可由e'd和e'g推导出来。

4)同步发电机的3阶模型

当忽略g、D、Q绕组的暂态过程时，只计及励磁绕组f的电磁暂态过程时，上述发电机的4阶模型将变为3阶模型。

5)同步发电机的2阶模型

当不考虑阻尼的影响且不考虑励磁电压变化的影响，有假定电势e'g和E'保持不变恒定的2种模型、其中E'保持不变恒定的模型称为经典模型，e'g则计及了发电机的凸极效应。

4 同步发电机各阶模型的模拟仿真

“电力系统分析”课程分为理论环节和实践环节。理论环节主要从发电机的原始方程通过派克变换推导出同步发电机的基本方程，从稳态运行和同步发电机三相短路过程推导出用空载电势、暂态电势、次暂态电势表达的发电机机端电压、电流的数学表达式。实践环节则有短路、稳定状态的仿真及动模实验，它涉及同步发电机各阶模型的使用。本文以PSD-BPA软件为工具，采用文献［6，7] 提供的3机9节点系统为例，其原理图如图3所示。发电机参数如表1所示。

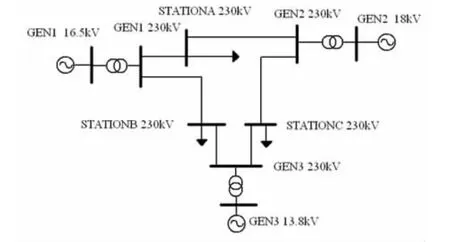
图3 3机9节点系统

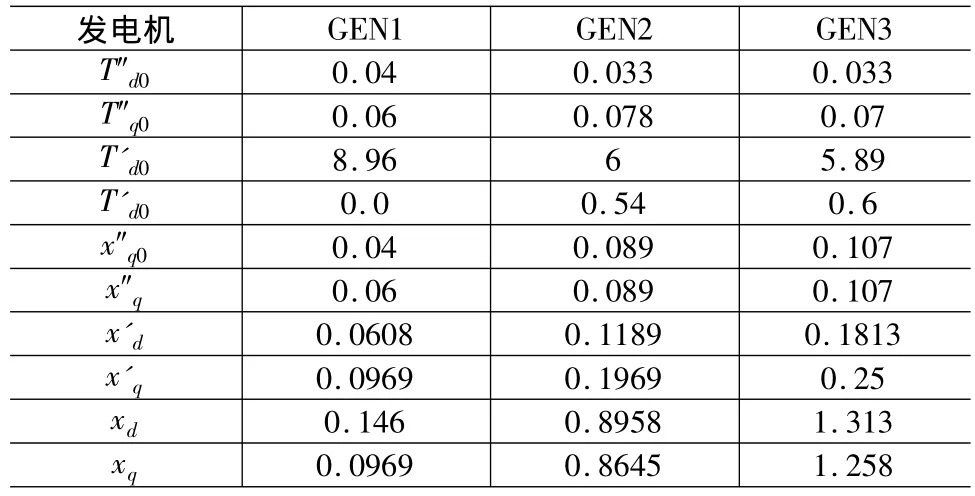
表1 发电机参数表

我们分别建立发电机GEN1的2阶、3阶和5阶模型，模拟仿真线路［STATIONB—GEN2(230kV)] 发生三相短路故障时的情况，结果如图4所示。

图4 发电机功角摇摆曲线图

它们所对应的极限切除时间如表2所示。

表2 发电机各阶模型对应的系统极限切除时间

从各阶发电机模型对电力系统暂态稳定的分析结果可以看出，采用不同模型其功角变化的趋势是一致的，但是从其趋于稳定的快慢是有差异的，由于高阶发电机模型详细计入阻尼绕组的电气阻尼，能更能详细地仿真功角的变化情况。因此在实际应用中应根据离线、在线和故障等不同情况进行选择，尽可能达到精度和速度的统一。

［1] 王敏，汪兴强，李生虎.“电力系统分析”学习的关键知识点［J] 南京:电气电子教学学报2008，Vol.30 No.2(52-56)

［2] 朱兰，韦钢，符杨等.“电力系统分析”课程教学及实践环节教学方法［J] 南京:电气电子教学学报2011，Vol.33.S1(128-133)

［3] 倪以信，陈寿孙，张宝霖.动态电力系统的理论和分析［M] .北京:清华大学出版社

［4] 刘天琪邱晓燕.电力系统分析理论［M] 北京:科学出版社2005.

［5] 夏道止.电力系统分析(下册)［M] 北京:水利电力出版社，1995.

［6] 印永华，卜广全.PSD-BPA潮流程序用户手册［R] .北京:中国电力科学研究院，2005.9.

［7] 印永华，卜广全.PSD-BPA暂态稳定程序用户手册［R] .北京:中国电力科学研究院，2005.9.