基于LS-DYNA的Lagrange网格与SPH鸟撞分析对比研究

王昌银，滕春明，彭志军

（中航工业洪都，江西南昌330024）

0 引言

随着新一代雷达技术的发展和环境保护越来越受到重视，飞机低空、高速飞行任务增加，鸟撞飞机的概率也随之增加。鸟撞飞机带来的危害已越来越为人们所认识。20世纪60年代后，西方主要国家纷纷开展鸟撞飞行器的研究。

鸟撞问题的实质可归结为瞬态动力学问题，鸟体的动量和动能的传递在极短的时间（毫秒极）内完成，由此会产生巨大的撞击力。在撞击的过程中鸟体的形状及物理参数会发生很大的变化，鸟体与结构之间会发生耦合作用，鸟体的模拟对鸟撞分析的结果有很大的影响，因此鸟体的模拟是鸟撞分析的重点。目前主要采用数值分析软件有LS-DYNA、DYTRAN和PAM-CRASH。它们均能较真实的模拟鸟体撞击飞机的全过程。

近年来，飞机抗鸟撞性能动力学分析中鸟体模型的模拟逐渐从传统的Lagrange网格过渡到现在的SPH。本文基于LS-DYNA软件，通过某型教练机风挡抗鸟撞性能仿真分析，分别采用Lagrange网格与SPH模拟鸟体进行鸟撞对比分析，对比分析Lagrange网格、试验实测结果与SPH之间的差异，表明SPH在鸟撞分析中是可行的，并且可以解决动力学大变形的问题。

1 Lagrange网格和SPH对比

1.1 Lagrange网格介绍

传统的Lagrange[1]有限元网格将节点固定在分析对象上。通过连接有关节点形成单元，再由单元组成网格。当分析对象变形时，节点随着材料的移动而移动，同时单元也随之变形。

1.2 SPH介绍

SPH是Lucy等于1977年提出的一种无网格粒子法，在连续体的破碎与分离分析中得到了应用。在解决极度变形和破坏类型的问题上，SPH有着其他方法无法比拟的优势。

SPH的核心是一种插值技术。每一个粒子“i”与其相距一设定距离范围内的所有其他粒子“j”发生相互作用，它们间的相互作用是由未知函数来衡量的。

理论上，任意粒子“i”的连续函数的值或其导数可以利用周围粒子“j”的已知值通过未知函数δ(x-x′)表示：

上式中：f(x)为三维坐标向量x的函数；Ω为包含的积分体积；δ(x-x′)为狄克拉函数，其性质如下：

δ(x-x′)函数在数值计算中难以实现，需要其他连续函数来近似，如果用光滑函数ω(x-x′,h)来取代函数 δ(x-x′)，则f(x)的积分表达式可写为：

其中，核函数[3]ω(x-x′,h)是粒子x 和x′之间的距离和光滑长度h的函数，核函数应该满足非负性、归一性、衰减性核区域性等条件。

1.3 Lagrange网格和SPH对比

Lagrange网格的主要优点是能够非常精确地描述结构边界的运动。缺点是在处理大变形问题时，将会出现严重的网格畸变现象。

Lagrange网格在求解大变形问题时，比如撞击到非光滑面时，鸟体网格可能会出现严重的扭曲，网格扭曲会引起显式时间积分步长过短，大大增加计算时间甚至导致计算终止。如图1所示，Lagrange网格的鸟体正面对中撞击有棱角的结构时，Lagrange网格的鸟体中间变形较大，会导致鸟体两侧的网格可能撞击不到被撞击物，导致计算结果与真实结果产生较大误差。

SPH则是把每个粒子作为一个物质的插值点，该方法可以避免鸟体在高速撞击时产生大的变形导致计算终止。

图1 Lagrange网格的鸟体撞击变形示意图

SPH的优点是不用网格，减少了有限元法中单元划分的工作，也没有网格畸变的问题。缺点是由于SPH是一门新的数值仿真分析方法，缺少坚实的理论基础和数学证明，现在对SPH方法的工程和数学问题的研究还不够。

2 仿真分析结果对比

本文通过PATRAN建立某型教练机风挡模型及鸟体模型，将模型输出到K文件，再用文本编辑器修改K文件相应的关键字，分别生成Lagrange网格和SPH粒子的计算文件，然后提交LS-DYNA计算求解，计算结果通过LS-PREPOST处理。

2.1 鸟体模型

鸟体的尺寸按照GJB2464-95（飞机玻璃抗鸟撞试验方法）中的要求简化为长径比为2：1的圆柱体。鸟体密度为970kg/m3，重量为1.8kg，即长度为0.212m，直径为0.053m。鸟体的Lagrange网格模型和SPH模型见图2。

图2 Lagrange网格模型和SPH粒子模型

为了对比两种模型计算结果的差异，Lagrange网格鸟体材料与SPH粒子鸟体材料采用相同的材料，即两种方法均采用可压缩泡沫材料。鸟体材料参数见表1。

2.2 风挡模型

某型教练机风挡材料为航空YB-DM-3有机玻璃，有限元模型中采用随动塑性材料模拟玻璃，风挡网格采用二维平面壳单元模拟，玻璃厚度为18mm。风挡材料属性见表1，风挡有限元模型见图3。

表1 材料属性表

风挡四周通过螺栓与机身连接，模型中约束风挡四周的节点在三个方向上的平动自由度。

图3 风挡有限元模型

2.3 分析结果

有限元模型中的接触算法采用点面接触，即*CONTACT_NODES_TO_SURFACE。根据鸟撞试验结果分析该风挡可承受1.8kg鸟体正面撞击不发生破坏的临界速度约为450km/h。因此在仿真分析时，选取鸟体的撞击速度为450km/h，被撞击中心点取为风挡对称线中点。分析结果中取被撞击中心点位置的单元应力或者节点位移进行对比分析，Lagrange网格和SPH计算得出的被撞击点处的单元应力-时间曲线见图4，两种方法计算得出的被撞击中心点的位移-时间曲线见图5，两种方法计算得出的撞击力-时间曲线见图6。

2.4 分析结果对比

通过图4和图5可以看出两种鸟体模型计算得出的被撞击风挡单元严重应力和严重位移结果趋势基本一致，SPH模型计算得出的峰值（应力、位移、撞击力）时间均比Lagrange网格要稍微延迟。

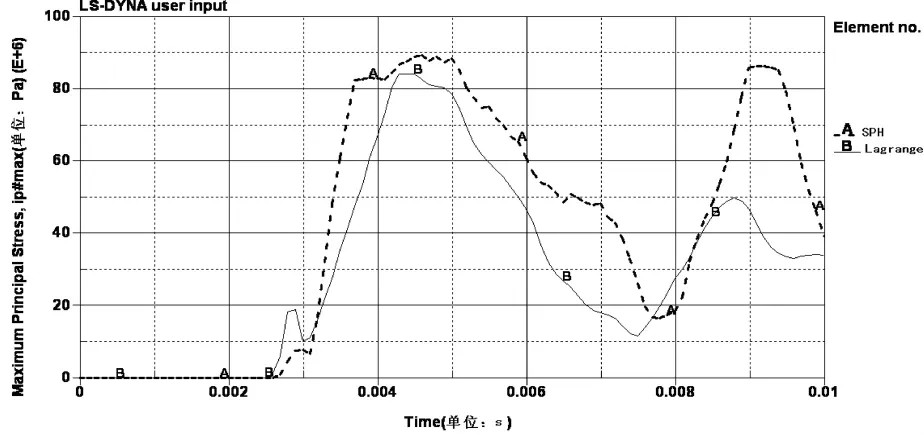
图4 应力-时间曲线

图5 位移-时间曲线

图6 撞击力-时间曲线

两种鸟体模型计算出的结果与试验实测数据对比见表2，由表2可以看出有限元仿真分析结果与试验实测结果吻合较好，表明在鸟撞分析中，Lagrange网格和SPH均可以使用。Lagrange网格模型与SPH模型使用相同的材料属性时，Lagrange网格计算得出的最严重应力、最大位移、最大撞击力均比SPH计算得出的相应结果低，且Lagrange网格模型计算结果与试验结果更为接近。Lagrange网格模型中使用的鸟体材料属性是经过多次试验实测结果修正后形成的经验数据，SPH模型中只是简单的继承了Lagrange鸟体的材料属性，模拟鸟体的方法不同而鸟体的材料属性相同可能是导致分析结果不同的原因，如果使用试验实测数据对SPH中的材料属性进行修正，可以减小SPH模型分析结果与试验实测结果的误差。

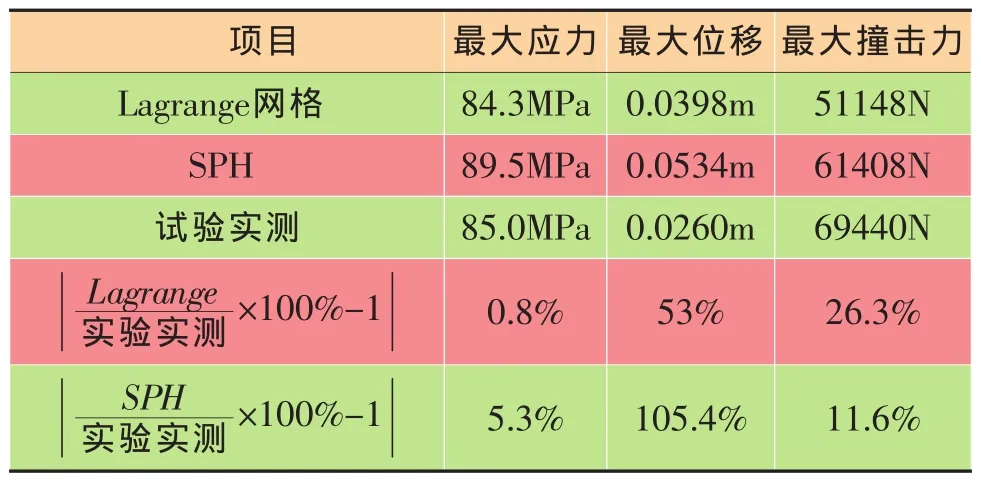
表2 计算结果对比

3 结论

通过分别采用Lagrange网格和SPH模拟鸟体进行鸟撞性能仿真对比分析表明：

1）SPH可以解决动力学撞击中的大变形问题。

2）SPH计算得出的结果与Lagrange网格计算得出的结果趋势基本相同，前者的计算结果比后者的计算结果偏严重，两种方法与试验实测结果基本吻合。

3）使用试验实测数据对SPH鸟体材料属性进行修正，可以减少分析结果与试验数据的误差。

[1]丁沛然，钱纯编著．非线性瞬态动力学分析MSC.Dytran理论及应用[M]．北京：科学出版社，2006．

[2]白金泽编著．LS-DYNA3D理论基础与实例分析[M]．北京：科学出版社，2005．

[3]孔令勇，宋春燕，李娜 著．基于SPH方法某飞机典型结构鸟撞分析研究[C]．北京：振动工程学报，2012:97-100．

[4]郝好山，胡仁喜，康士廷 等著．ANSYS 12.0 LS-DYNA非线性有限元分析从入门到精髓[M]．北京：机械工业出版社，2010．