地震模拟振动台基础动力反应的比较研究

王磊，丁海平

(江苏省结构工程重点实验室(苏州科技学院)，江苏 苏州 215011)

0 引言

地震模拟振动台在工作时相当于一个大的震源，具有推力大、工作频率范围宽等特点，其基础不可避免地会发生共振，而且共振时的破坏力很大，若设计不当，可对周围的建筑物和设施造成很大的危害。在振动台基础振动特性方面，文献［1］对加州大学伯克列分校振动台基础的研究认为:振动台低频段激振力主要由地基刚度抵抗;共振时，由地基刚度和阻尼比共同作用;而20 Hz以上的较高频激振力主要由基础质量起作用。文献［2］认为基础的质量宜控制在台面质量和试件最大质量总和的50倍，以满足振动控制要求。

当前，地震模拟振动台基础设计尚无规范方法，国内许多振动台基础的动力计算和设计参考了动力机器基础设计方法［3－4］，如，GB 50040—1996《动力机器基础设计规范》［4］方法(以下简称《规范》方法)，拉普拉斯(Laplace)变换方法［5］，基于弹性半空间理论的地基阻抗函数法［6］，等等，但应用不同方法所计算的振动台基础动力响应有什么差异，哪种方法能更准确地反映基础振动特性等方面的研究还较少。本文针对苏州科技学院拟建的6 m×8 m三向六自由度地震模拟振动台基础，分别应用《规范》方法、拉普拉斯变换法和动力阻抗法，在频域范围内计算其动力响应，并对其结果进行比较和分析。

1 地震模拟振动台基础设计

苏州科技学院拟建一座6 m×8 m三向六自由度地震模拟振动台，振动台台面重量40 t，设计试件重量 70 t，x、y、z方向最大加速度分别为1.5g、1.2g、1.0g;工作频率0.1 ～50 Hz。

基础拟建场地覆盖层厚度＞50 m，以黏性土和粉土为主。建筑场地类别划为Ⅲ类，抗震设计所用特征周期值为0.45 s。另据钻探实测，20.0 m深度内土层的等效剪切波速vse=154.6～155.4(m/s)。

根据拟建地震模拟振动台基本情况，结合场地勘探报告，设计振动台基础为实体式埋置基础，具体形式和尺寸如图1所示。

根据振动台基础的作用力系分析方法，计算得到振动台基础的受力情况。

平移作用力:

Fx=1 617 kN

Fy=1 294 kN

Fz=1 078 kN

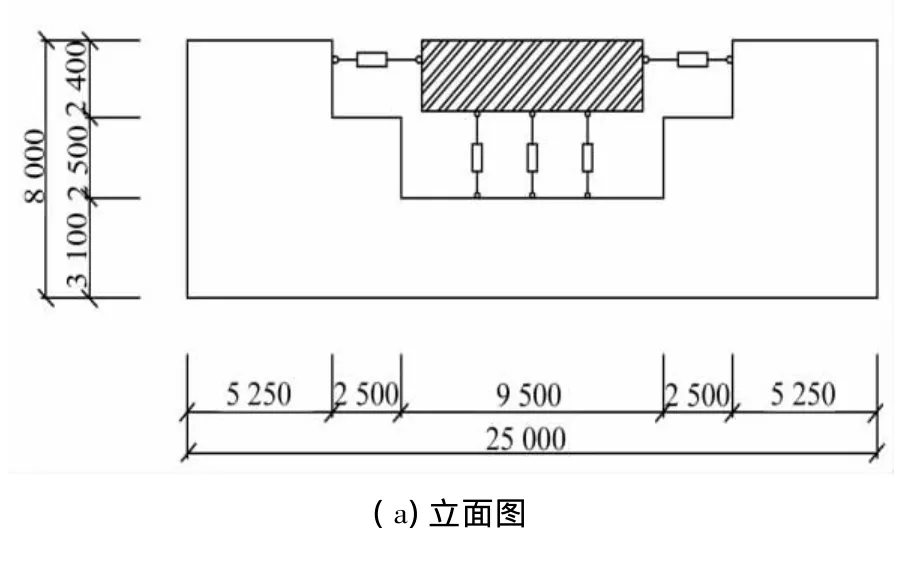
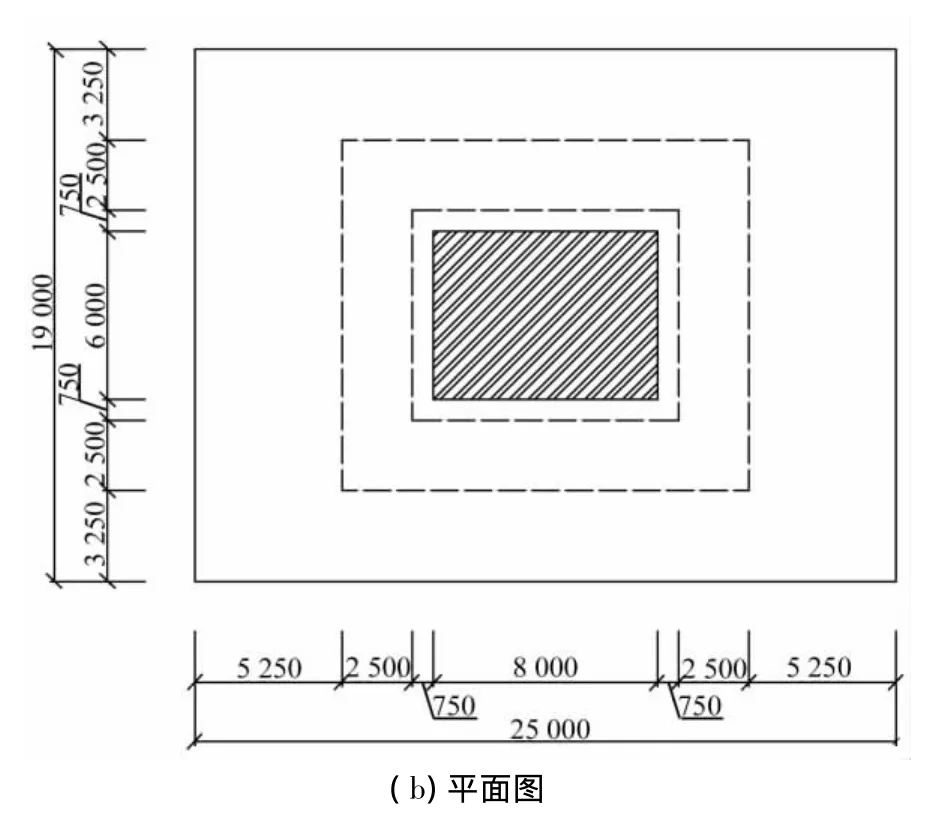
图1 振动台基础立面图和平面图

转动力矩:

mφ=8 743 kN·m

mφ=10 858 kN·m

mψ=741 kN·m

按照将基础分为几个规则图形分区计算的方法，确定该基础的几何参数。

质量:

M=7 812 t(约为台面和试件质量之和的71倍)

转动惯量:

Jx=295 774 t·m2

Jy=503 885 t·m2

Jz=722 879 t·m2

基础埋深为8．0 m，持力层为粉质黏土，承载力特征值fak=150 kPa，经验算，地基承载力满足GB 50007—2002《建筑地基基础设计规范》［7］要求。

2 振动台基础动力反应

2.1 采用不同方法计算的基本参数

地基刚度、阻尼等基本参数的计算是求解振动方程、分析振动台基础动力反应的前提，《规范》方法、拉普拉斯变换法和动力阻抗法分别采用不同的方式计算基本参数。

《规范》方法依据天然地基的抗压刚度系数，加权计算影响深度内，由不同土层组成的地基土的抗压、抗弯、抗剪、抗扭刚度系数;对阻尼比，《规范》方法认为这是与基组质量比的平方根成反比的常数。拉普拉斯变换法是依据弹性半空间理论实用化方法——Lysmer比拟法［8］计算地基刚度、阻尼等参数。动力阻抗法计算基本参数，关键在于地基阻抗矩阵 KS［9］的选取，文献［10］～ 文献［12］分别给出了矩形截面埋置基础的阻抗函数解析解，其研究结果基本吻合，本文选取了文献［10］的研究成果。

针对上述设计的振动台基础，分别采用3种不同的方法计算基础各个自由度对应的地基刚度K(x、y、z方向的单位为 N/m;φ、φ、ψ 方向的单位为N·m/rad)、固有频率 ω(rad)和阻尼比 D，具体数值如表1所示。

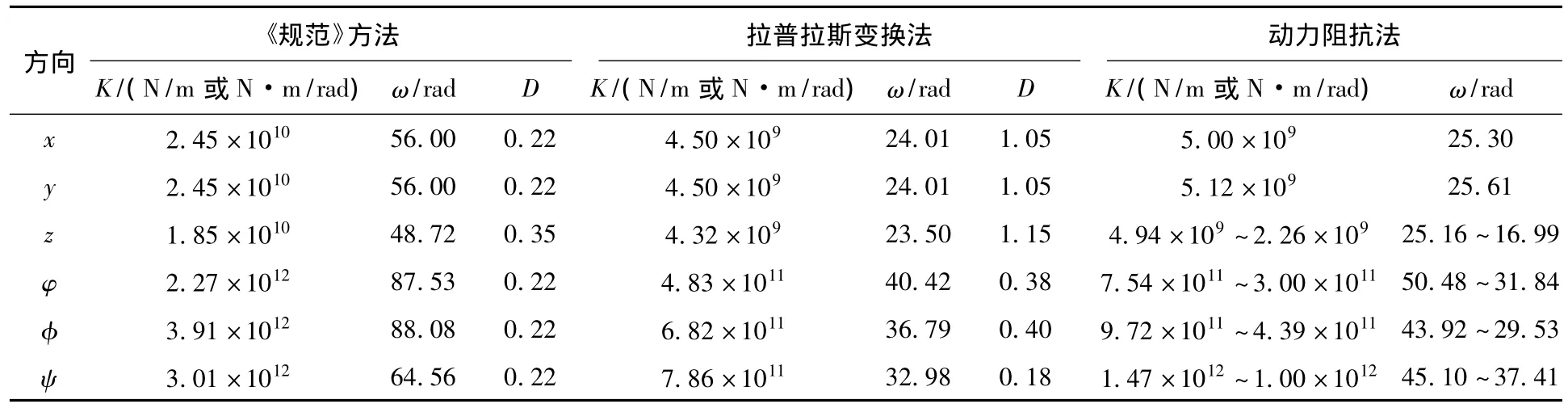
表1 按照不同方法计算出的基本参数

由表1可见，按照拉普拉斯变换法和动力阻抗法计算出的地基刚度和固有频率基本相同，但明显小于《规范》方法的计算结果。另外，拉普拉斯变换方法计算的地基阻尼比大于《规范》方法的计算结果。出现这一现象的主要原因有:一是由于拉普拉斯变换法和动力阻抗法都是基于弹性半空间理论，二是由于《规范》方法是根据压缩机、破碎机等动力机器基础设计经验确定地基动力参数，应用于大面积扁平型振动台基础时，会使刚度计算结果偏大，阻尼偏小。

2.2 采用不同方法计算的加速度响应

对振动方程的求解，《规范》方法基于振动理论，分别给出了基组在竖向振动、扭转振动和水平回转耦合振动情况下，基组的自振频率及顶面控制点的动力响应计算公式。拉普拉斯变换法利用拉普拉斯变换微分性质，将振动方程降阶为关于x(s)、y(s)、z(s)、φ(s)、φ(s)、ψ(s)的六元一次方程组，得到它们关于外频率 ω的表达后，在0．1～50 Hz频率范围内，再对其作拉普拉斯逆变换运算，即可得到基础质心在不同频率下的动力响应。动力阻抗法假定外荷载、动反力、动力响应均为稳态形式，其中动反力表示成动力阻抗的函数，代入垂直振动、扭转振动、耦合振动平衡方程，得到基础质心六个自由度的响应幅值。［6］

在计算出地基刚度、阻尼等基本参数后，分别采用《规范》方法、拉普拉斯变换法和动力阻抗法，分析所设计振动台基础的动力响应，绘出不同振动类型下基础的加速度频响曲线，如图2～图5所示。

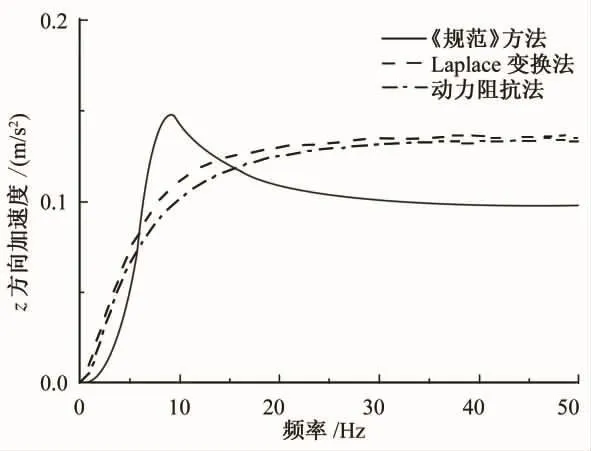
图2 垂直振动引起的加速度响应

由图2～图5可知:

1)在低频区(约＜10 Hz)，《规范》方法计算的振动台基础加速度响应低于拉普拉斯变换方法和动力阻抗法。因为激振力频率处于这一区段时，激振力主要由地基刚度抵抗，而《规范》方法计算的地基刚度明显大于拉普拉斯变换法和动力阻抗法。

2)在中频区(10 Hz～20 Hz)，《规范》方法共振更为明显，且加速度峰值对应的频率略大于拉普拉斯变换法和动力阻抗法。因为激振力频率处于这一区段时，激振力由地基刚度和阻尼比共同抵抗，而《规范》方法计算的阻尼比相对较小，固有频率相对较大。

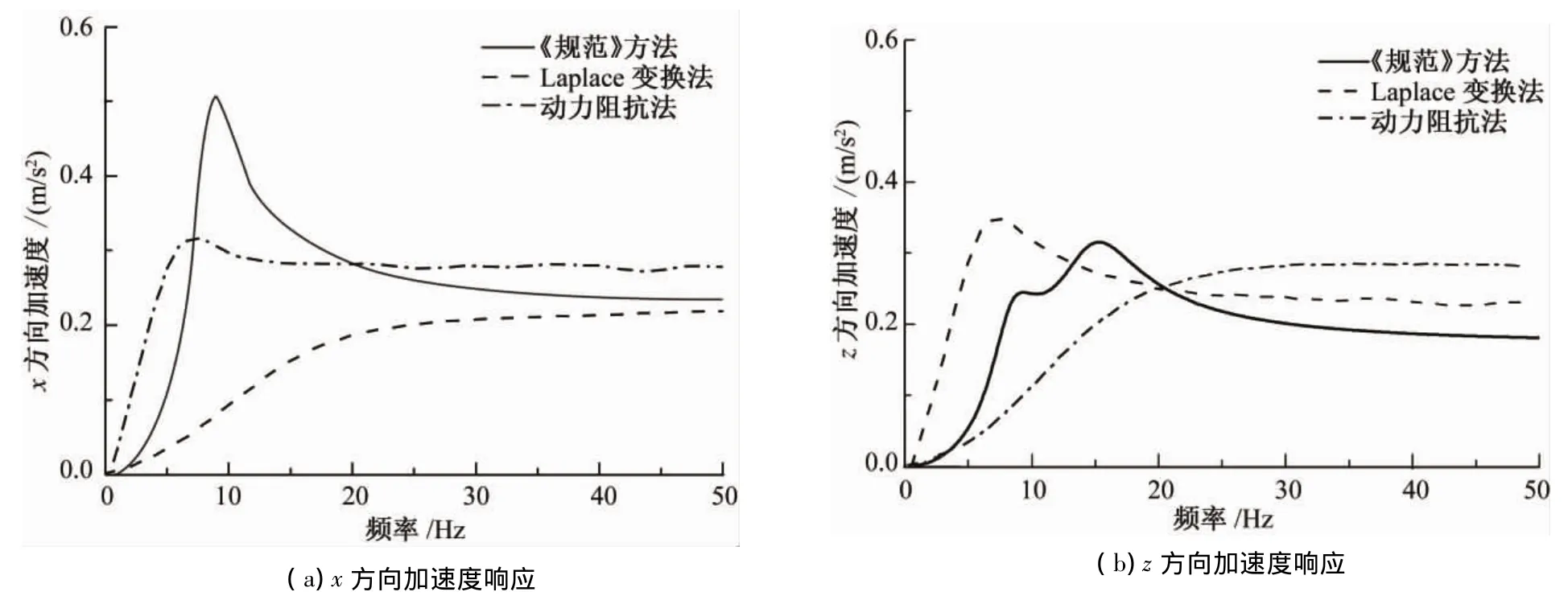
图3 沿x方向水平绕y轴回转耦合振动引起的加速度响应

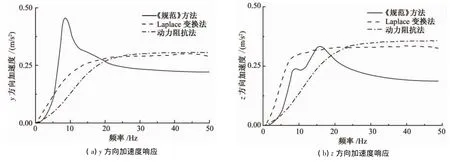
图4 沿y方向水平绕x轴回转耦合振动引起的加速度响应

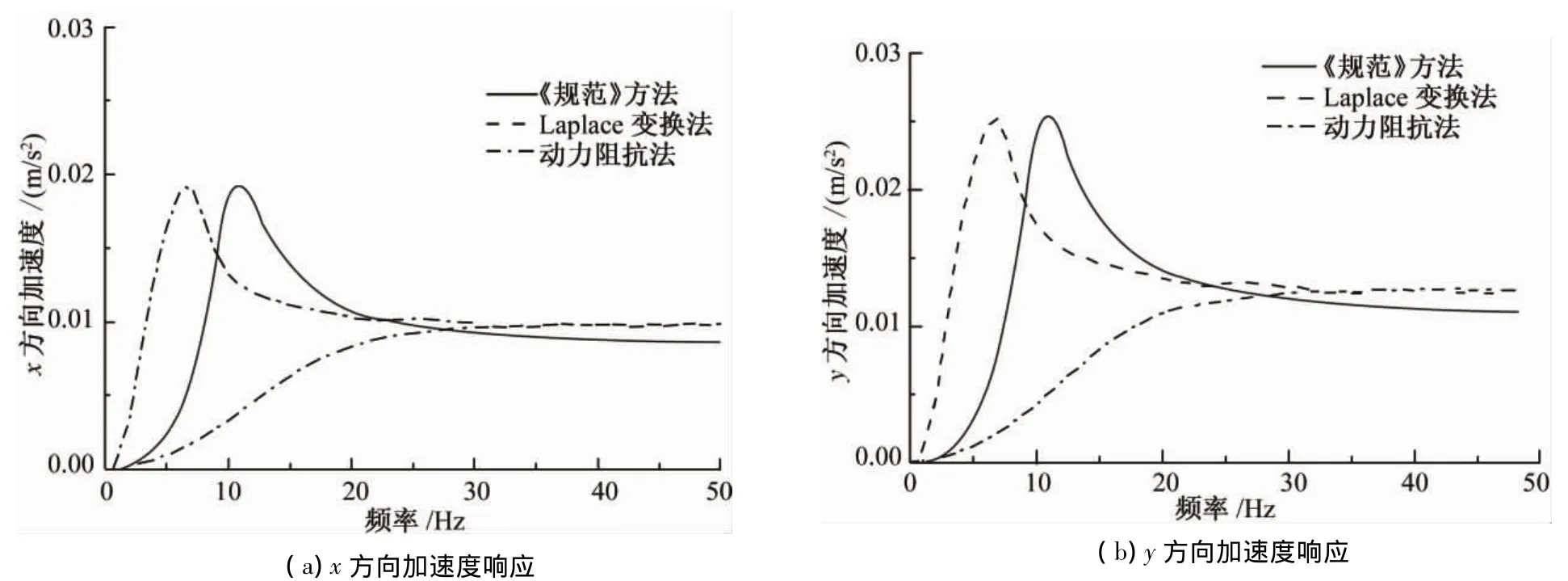
图5 扭转振动引起的加速度响应

3)在高频区(约＞20 Hz)，除了耦合振动只考虑基础的第一、第二振型的回转角位移导致垂直向加速度偏低外，3种方法所得到的加速度响应基本一致，差别控制在15%以内。因为激振力频率处于这一区段时，激振力主要由基础质量抵抗，故不同方法计算出的加速度响应差别不大。

3 结论

采用《规范》方法、拉普拉斯变换方法和动力阻抗法，对三向六自由度地震模拟振动台基础进行了动力响应分析、研究和比较，并得出以下结论:

1)由于拟建地震模拟振动台所在地区按地震烈度Ⅶ度设防，因此振动台基础以加速度小于0.1g作为振动控制要求。该设计的25 m×19 m×8 m实体式振动台基础，根据《规范》方法、拉普拉斯变换法、动力阻抗法进行动力响应分析，均满足振动控制要求。

2)由于振动台的最高工作频率通常大于30 Hz，工作频率跨越了低频区、中频区和高频区，因此，振动台基础宜按最大动力反应和设计分析。《规范》方法计算的地基刚度偏高，阻尼比偏低，最大动力反应高于拉普拉斯变换方法和动力阻抗法，这一现象在动力反应最大的耦合振动情况下更为明显。综合考虑安全性和经济性，对振动台基础设计分析时，建议根据文献［4］确定地基刚度，参照Lysmer比拟法计算阻尼，采用文献［4］中给出的公式或对振动方程进行拉普拉斯变换的方法计算动力响应。

［1］Dixon Rac，Penzien Joseph．Dynamic Response of a 20ft20ft Shaking Table［C］//In:Proceedings of the 5th WCEE，Rome:［s．n］，1973，2:1725 －1752．

［2］方重．大型地震模拟振动台主要参数的确定及技术经济分析［J］．世界地震工程，2001，17(4):135 －138．

［3］张自平，程绍革，贺军．三向六自由度大型模拟地震振动台基础动力分析计算［J］．建筑科学，2004，20(2):36 －40．

［4］国家技术监督局，中华人民共和国机械工业部．GB 50040—1996动力机器基础设计规范［S］．北京:中国计划出版社，1997．

［5］黄浩华．地震模拟振动台的设计与应用技术［M］．北京:地震出版社，2008．

［6］侯兴民，廖振鹏，黄浩华．动力基础频域响应分析［J］．工程力学，2003，20(4):122 －127．

［7］中华人民共和国住房和城乡建设部，中华人民共和国国家质量监督检验检疫总局．GB 50007—2011建筑地基基础设计规范［S］．北京:中国建筑工业出版社，2012．

［8］严人觉，王贻荪，韩清宇．动力基础半空间理论概论［M］．北京:中国建筑工业出版社，1981．

［9］廖振鹏．工程波动理论导引［M］．2版．北京:科学出版社，2004．

［10］Pais Artur，Kausel Eduardo．Approximate Formulas for Dynamic Stiffness of Rigid Foundations［J］．Soil Dynamics and Earthquake Engineering，1988，7(4):213 －227．

［11］Dominguez J．Dynamic Stiffness of Rectangular Foundation［R］．Report No．R 78 － 20，Dept．of Civil Engineering，MIT．Ma，1978．

［12］Wong H L，Luco J E．Dynamic Response of Rigid Foundations of Arbitrary Shape［J］．Earthquake Eng．and Struct．Dynamics，1976，6:3 －16．