基于人工蜂群的交通信号自适应优化控制

郭新兰，李涛

(1．南京交通职业技术学院机电工程系，江苏 南京 211188;2．华为技术有限公司，江苏 南京 210012)

0 引言

城市交通信号作为一个具有极强随机性的问题，利用经典控制方法(如，定时控制［1］)，交通信号配时很难达到一个比较优化的结果，尤其是当交通流出现较大随机波动时就更加困难。为了实现区域交通网的有序控制，需要将各路口的控制协调起来，以防止交通拥塞。在交通信号协调控制研究方面，绿波带方法［2］最先得到发展。但是，绿波带方法要达到良好的控制效果有许多假定性约束，限制了绿波带方法的实际使用效果。近几十年来研究者尝试将不同的人工智能技术应用于交通信号的控制中，如，神经网络［3］、模糊逻辑［4］。由于其中的一些算法结构复杂且有大量参数需要调整，因此使得相应的算法难以达到很好的控制效果。

Werbos将强化学习和动态规划相结合提出了一种新的优化技术——自适应动态规划(A-daptive Dynamic Programming，ADP)。［5］在自适应优化期间，由于自适应动态规划网络除了期望目标，不需要知道具体的路径信息，因此更适合随机应用环境。

从已有文献可知，ADP算法中的主要模块由人工神经网络构成，模块通过梯度下降法训练、调整网络参数，采用梯度下降法进行人工神经网络训练时存在一些固有问题，造成ADP模块训练效果的不理想。与此同时，群智能算法的发展及其在寻优领域的应用展现出此类算法的优越性。［6－9］群智能依靠概率搜索算法，与梯度方法及传统的演化算法相比，群智能方法易于实现，算法中仅涉及基本的数学操作，其数学处理过程对CPU和内存的要求不高，且该方法只需要目标函数的输出值，而无需其梯度信息。

该研究首先介绍由Karaboga［10］提出的人工蜂群理论;其次进一步将人工蜂群理论用于ADP算法中神经网络参数的优化学习，提出改进的ABADP算法，借助人工蜂群理论的优点来提高神经网络的学习速度，以便尽快取得优化控制效果;最后将ABADP算法用于单交叉路口的交通信号控制问题，验证所提出算法在学习速度上的优势，并通过仿真结果证明基于人工蜂群理论的ADP算法可以提高ADP算法的学习效率。

1 交叉路口基本模型

通常交通信号控制的目标是最小化车辆通过路口的平均延误。典型的十字交叉路口交通流示意图如图1所示。作为简化情况，右转车流可以不加考虑，因此，本文考虑4个控制相位(南北直行、南北左转、东西直行、东西左转)，四相位定义如图2所示。

假定1 s内最多有1辆车到达，因此在某一秒内车辆的到达状态定义为:

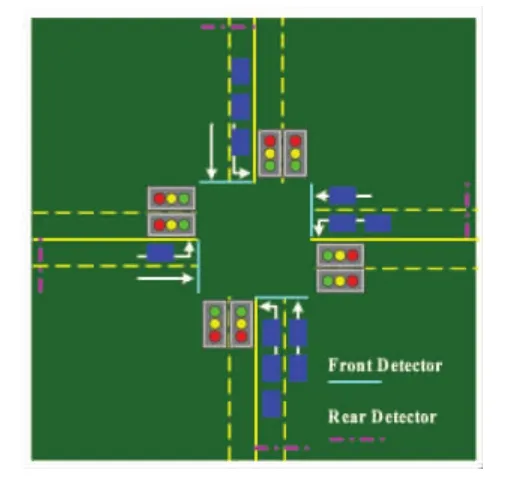
图1 交叉路口模型

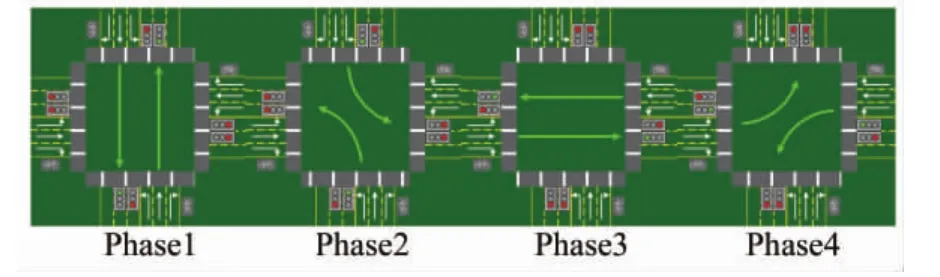
图2 四相位定义

所涉及的交通状态变量，如道路队列长度和等待时间仿照Pappis的定义［6］如下。

在(t，t+Δt)时间区间内进入某一车道的车辆数为:

假设车辆以s辆/s的速度通过路口，则在(t，t+Δt)时间区间内离开某条道路的车辆数为:

(t，t+Δt)时间区间内处于红灯状态的任一条车道的车辆队列数为:

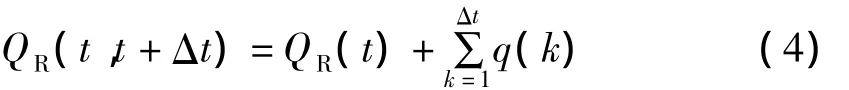
(t，t+Δt)时间区间内处于红灯状态的任一条车道的车辆总体延误时间为:

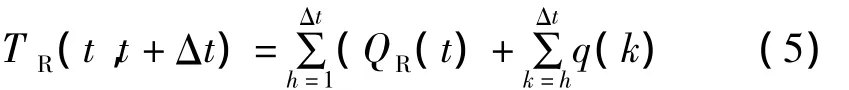
(t，t+Δt)时间区间内处于绿灯状态的任一条车道的车辆队列数为:

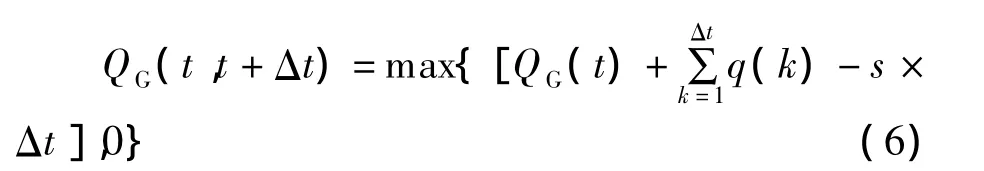
(t，t+Δt)时间区间内处于绿灯状态的任一条车道的车辆总体延误时间为:

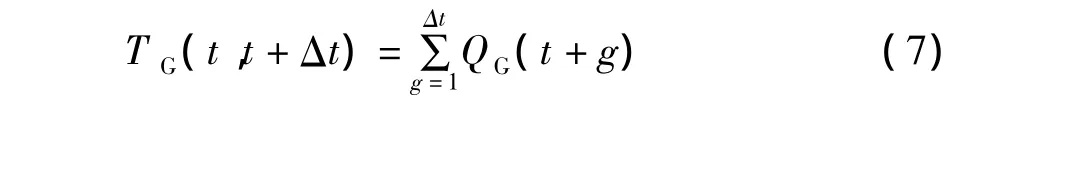
某一时段的平均车辆延误时间为:

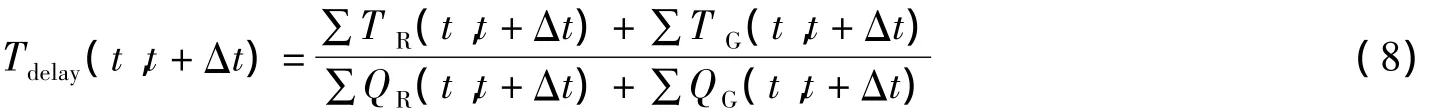
2 基于ADP的交通信号控制算法

图3为所设计在线学习式控制算法的结构框图。执行网络实现对相位的控制，评价网络用来评价控制效果，并以此调整两网络的参数，以实现优化控制的目的。在图3中x(t)是输入向量，由每个相位中车道最大排队长度组成，r(t)是算法学习的强化信号量，实线代表信号的流向，虚线代表修正参数的流向。

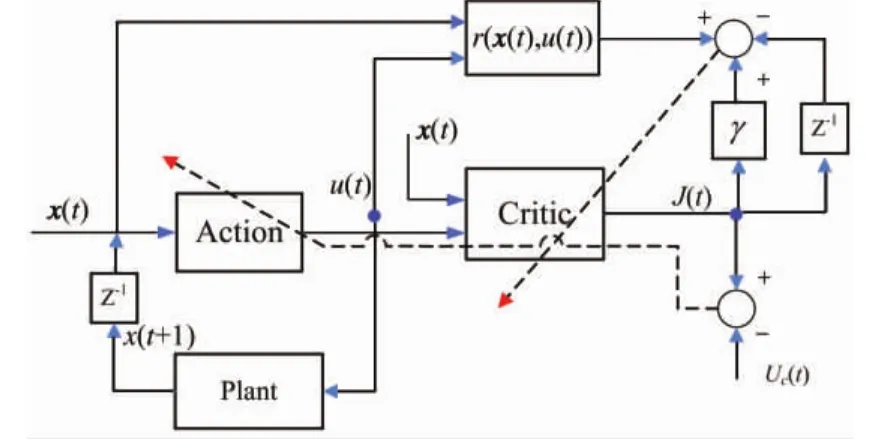
图3 ADHDP算法框图

图3中r(x(t)，u(t))为瞬时效用函数，0＜γ＜1为折扣因子，J(t)为状态x(t)的cost-to-go函数，u(t)为控制序列，Uc(t)为控制目标。

所设计控制算法中，假设由相位i开始控制，首先分配最小绿灯时间(minGreen)，当相位i所分配的绿灯时间快用完时，由Action模块进行交通信号决策，决定是延长当前绿灯相位的绿灯时间还是结束此绿灯相位。如果算法决定终止当前绿灯相位或当前绿灯相位累积分配的绿灯时间达到最大绿灯时间(maxGreen)，则将绿灯切换到下一相位。Critic模块根据所采集的交通数据和控制效果对Critic模块和Action模块进行参数优化。所设计的ADHDP算法中的执行网络和评价网络的结构和学习策略如下所述。

2.1 Action模块

图4为Action网络结构图。在ADP信号控制算法中，执行网络和评价网络均采用三层人工神经网络来实现。

Action采用三层神经网络，输入变量为相位i(i=1，2，3，4)中最长的车辆队列长度，输入变量按照相位1→相位2→相位3→相位4→相位1的顺序进行循环变化;输出变量u(t)用以决定是否延长当前绿灯相位的绿灯时间。

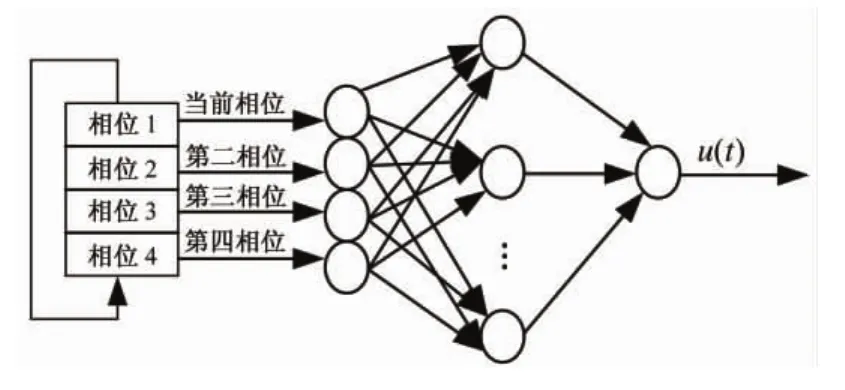
图4 Action网络结构图

训练目标为使系统性能指标J^(t)逼近控制目标Uc(t)，需将如下误差最小化:

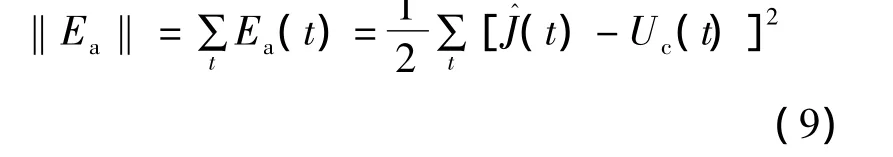
对于交通信号控制问题，控制目标是最小的平均车辆延误Tdelay(t)。为了使在不同交通流状况下取得最小车辆等待时间Tdelay(t)，且减小学习过程的盲目性，本文采取逐步降低目标值的思路。ADP交通信号控制算法的控制输出u*(t)定义如下:

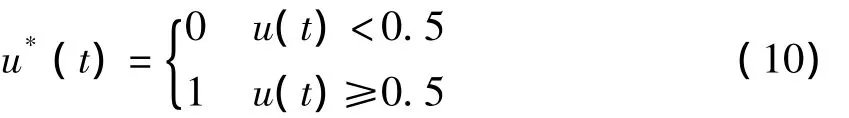
其中，u(t)为执行网络的输出，0表示终止当前的绿灯相位，反之，1表示延长当前绿灯相位。

2.2 Critic模块

图5所示的Critic模块由5个输入层节点、6个中间层节点和1个输出层节点组成。输入变量为对应的Action模块的输入变量xi(t)及Action模块的输出变量u(t);输出变量J^(t)用于逼近状态 x(t)的cost-to-go函数值J(t)。

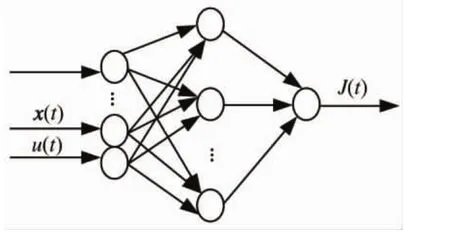
图5 Critic网络结构

在实际应用ADP算法中，发现瞬时效用函数r(x(t)，u(t)))在一定范围内变化时，可以取得较好的效果，因此，选取如下瞬时效用函数:

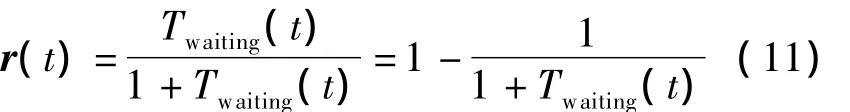
当车辆等待时间Twaiting在0～∞变化时，瞬时效用函数r(t)位于［0，1］区间。

3 基于人工蜂群理论改进ADP算法

人工蜂群理论是模拟蜜蜂觅食这一群体性智能行为而产生的。对于多变量数字优化问题，文献［10］提出了一种称之为人工蜂群理论(ABC)的仿蜂群算法，在非约束问题上的求解效果与其他著名的现代启发式算法，如，遗传算法(GA)、差分进化算法(DE)和粒子群算法(PSO)进行了比较，通过对Schaffer's F6等方程优化求解比较，结果显示，ABC理论在参数优化问题求解上具有优越性。［11］在人工蜂群理论中，蜜蜂被分成三个不同的种类:采集蜜蜂、观察蜜蜂和搜索蜜蜂。开始时，蜂群中采集蜜蜂数量(CN)和观察蜜蜂数量(ON)相等。在一次搜索过程中，探索和采集是同时进行的。在人工蜂群算法中，采集蜜蜂和观察蜜蜂执行采集任务，而搜索蜜蜂执行搜索新食物源的任务。

算法开始时人工蜂群理论产生一随机分布的初始解集P(G=0)，其中含有SN个解(食物源)。然后对解集进行循环迭代，用以模仿采集蜜蜂、观察蜜蜂和搜寻蜜蜂的搜索采集花蜜的过程。当所有的采集蜜蜂完成了搜索采集过程，它们与其他蜜蜂进行信息分享。任何一个观察蜜蜂对所有采集蜜蜂给出的食物源信息进行评价，并根据与某一食物源相关的概率值来选择一个食物源，其概率计算如下:

其中，fiti(x)，i∈{1，2，…，SN}代表解 i的适应度，它与i处食物源的花蜜数量成正比，代表这个解的好坏，食物源的质量越好，概率值越大，此食物源会被更多的观察蜜蜂选中;SN代表食物源的数量。

某个已有食物源i所能吸引到的观察蜜蜂数量Oi为:

其中，ON为观察蜜蜂的总数。

人工蜂群理论使用式(14)在已有食物源基础上产生候选食物源:

其中，k∈{1，2，…，SN}，j∈{1，2，…，D}随机选取，且 k≠i;φij是位于区间［－1，1］的一个随机数。

当一个采集蜜蜂变为搜索蜜蜂，通过产生一个随机解来代替被舍弃的解，以实现新食物源的搜寻，寻找一个新的食物源代替被舍弃的，这一过程通过式(15)来实现。

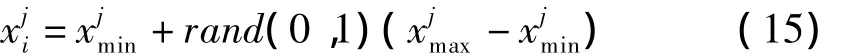
通过采集花蜜、改进已有食物源信息、舍弃质量差的食物源及搜索新的食物源等过程的不断循环，人工蜂群算法可以尽量减少落入局部极小点的可能性。

通过人工蜂群理论训练ADP算法的Action和Critic模块网络步骤如下:

1)一组可行的人工神经网络权重相当于人工蜂群算法中的一个食物源(解)，人工神经网络的训练误差类似于每个食物源的适应度。算法初始随机生成SN组神经网络权重作为采集蜜蜂的初始食物源，由采集蜜蜂评价各自食物源的质量(适应度)，并将此信息展现给所有观察蜜蜂。

2)观察蜜蜂根据得到的食物源质量信息选择跟随其中一个食物源，候选食物源(权重)的质量越好，此食物源吸引到的观察蜜蜂就越多。无法吸引观察蜜蜂的食物源(权重)被舍弃，由新生成的食物源(权重)代替。

3)完成信息传递后，采集蜜蜂在各自已有的神经网络权重附近生成新的权重，并根据前后两个神经网络权重的适应度，选取适应度较好的进行信息更新。同时，观察蜜蜂在自己选择的神经网络权重附近生成新的权重，同样根据前后两个神经网络权重的适应度优化选择，以进行信息更新。

4)采集蜜蜂和观察蜜蜂完成信息更新后，记录所有蜜蜂所拥有食物源(权重)中最好的。通过这一过程，适应度高的神经网络权重附近得到更多的搜索，加快了最优权重的搜索。

通过神经网络权重的适应度来吸引求解方向，实现搜索的启发功能，为了减小局部最优解的影响，蜜蜂独立进行信息更新，不受当前最优解的影响，以避免各食物源向局部最优方向发展。

考虑到人工神经网络的训练误差总是为正，为了避免适应度的大范围波动，将人工神经网络的训练误差进行转化，以用作人工蜂群算法中食物源的适应度计算公式:

食物源适应度的变化范围限制在［0，1］区间，相应的人工神经网络的训练问题转化为求解食物源适应度最大化的优化问题。在人工蜂群算法中，舍弃不合适食物源是搜索优化中的重要行为，其判断标准是:当某只采集蜜蜂由于所拥有的食物源质量太低，无法再召集观察蜜蜂时，即所提供的食物源信息被选取的几率为0时，此食物源被舍弃。相应的采集蜜蜂变为搜索蜜蜂，并按式(15)产生一随机解代替被舍弃的食物源，以保证食物源总数不变。

4 仿真研究和分析

为了验证基于人工蜂群算法改进的ADP算法的性能，将ABADP算法用于单交叉路口的交通信号控制问题，通过仿真来比较ABADP算法与传统ADP算法在交通信号控制方面的性能差异，同时与感应控制以及模糊控制［12］等进行比较，以验证控制效果。对于模糊控制选取的模糊规则参见文献［12］，选取当前绿灯相位的车辆排队长度和相邻红灯相位的车辆排队长度作为模糊控制器的输入。

仿真环境设置:仿真中的参数为绿灯延长时间7 s，最小绿灯时间15 s，最大绿灯时间50 s，每个相位的延误时间6 s。对ABADP算法和传统ADP算法在变化的交通流状况下分别试验5次，每种交通流状况下试验运行1 000个交通控制周期。Action模块和Critic模块的收敛指标分别为0.005和0.05，最大迭代次数分别为200次和150次，食物源数量、采集蜜蜂数量和观察蜜蜂的数量均选为30个。

控制效果及仿真结果如图6和表1所示。

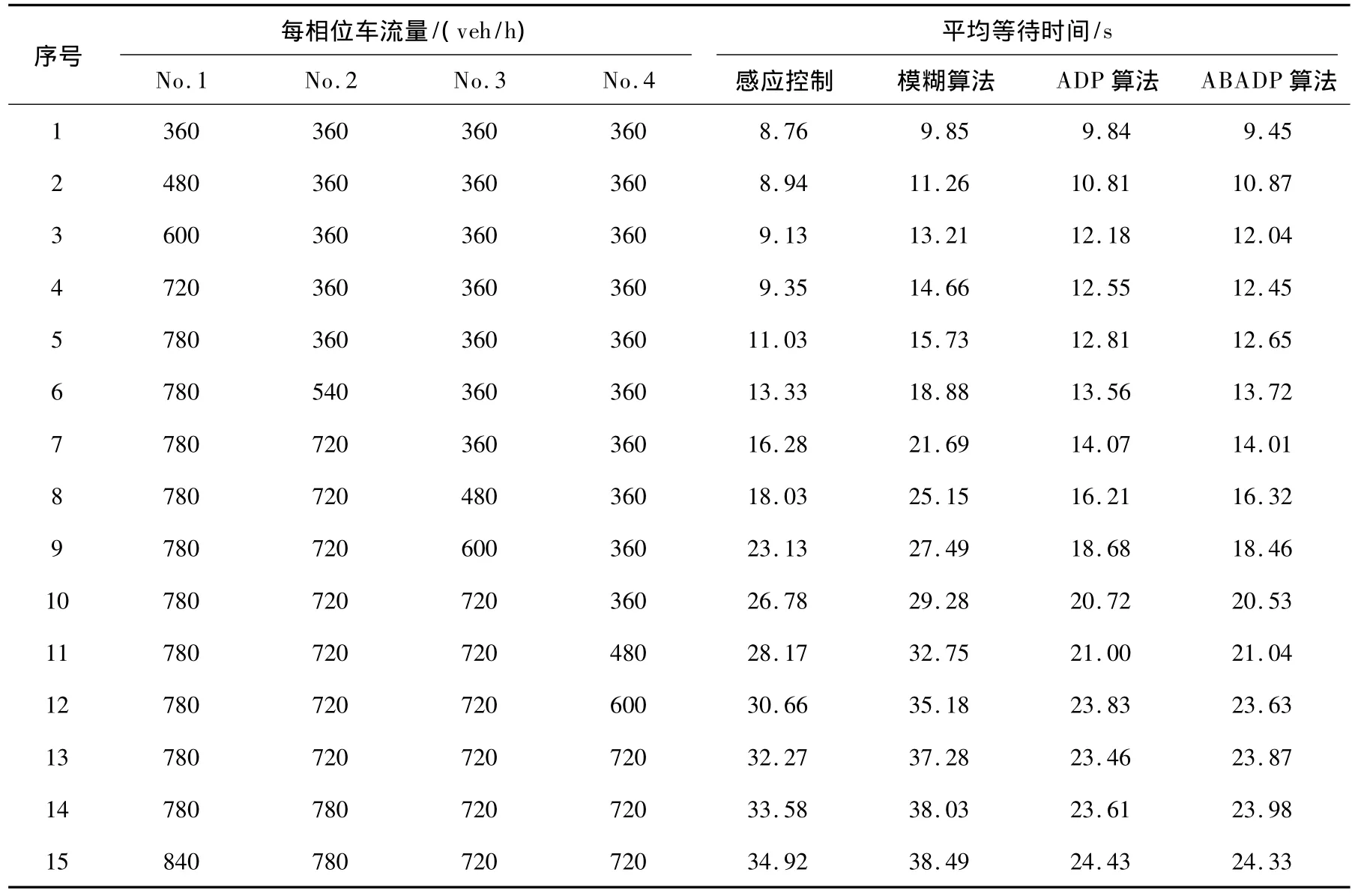
表1 不同控制算法的控制结果

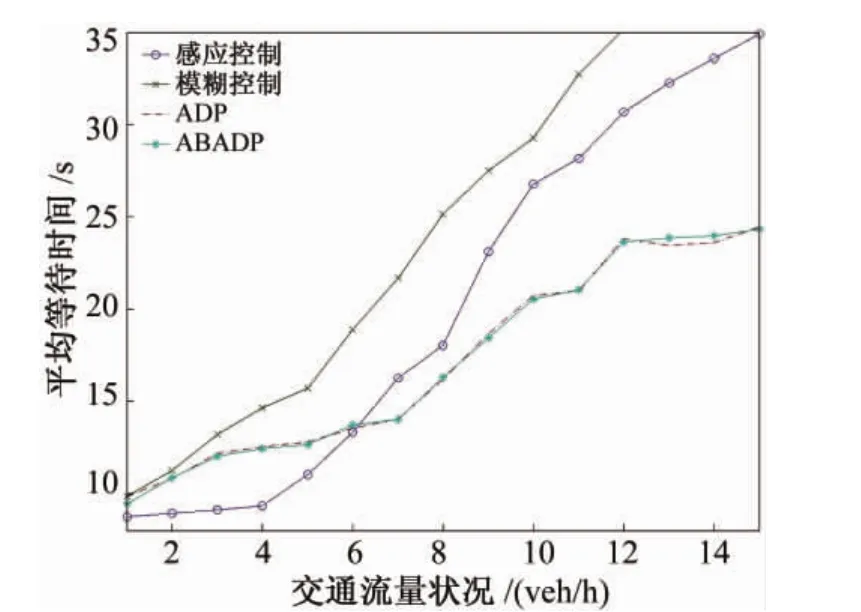
图6 不同控制算法仿真结果

由图6和表1可见，当各相位交通流量主次分明，且交通流量不大时，感应控制效果较好;当交通流量增大时，感应控制的控制效果变差。仿真中选取文献［12］所给出的模糊算法参数，由于模糊算法参数无法适用于任意系统状况，文献［12］中所设计的模糊控制器在本文仿真试验中效果不佳。在交通流量变大时，ADP交通信号控制算法较定时和模糊算法的车辆平均等待时间减少30% ～35%;较感应控制的车辆平均等待时间减少30%左右。

而对于ADP算法和ABADP算法对Action模块、Critic模块在不同交通流量下的训练次数和交通信号控制中车辆平均等待时间进行比较，仿真结果如图7和表2所示。由试验结果可见，由于Action模块的收敛指标选取比Critic模块要求高，相应的Action模块的平均训练次数要高于Critic模块的训练次数。对于Action模块的训练，ABADP算法比传统的ADP算法减少25%左右;对于Critic模块的训练，ABADP算法比传统的ADP算法减少70%左右。由于两者得到的优化参数性能近似，因此所取得的控制效果(平均车辆等待时间)近似相等。

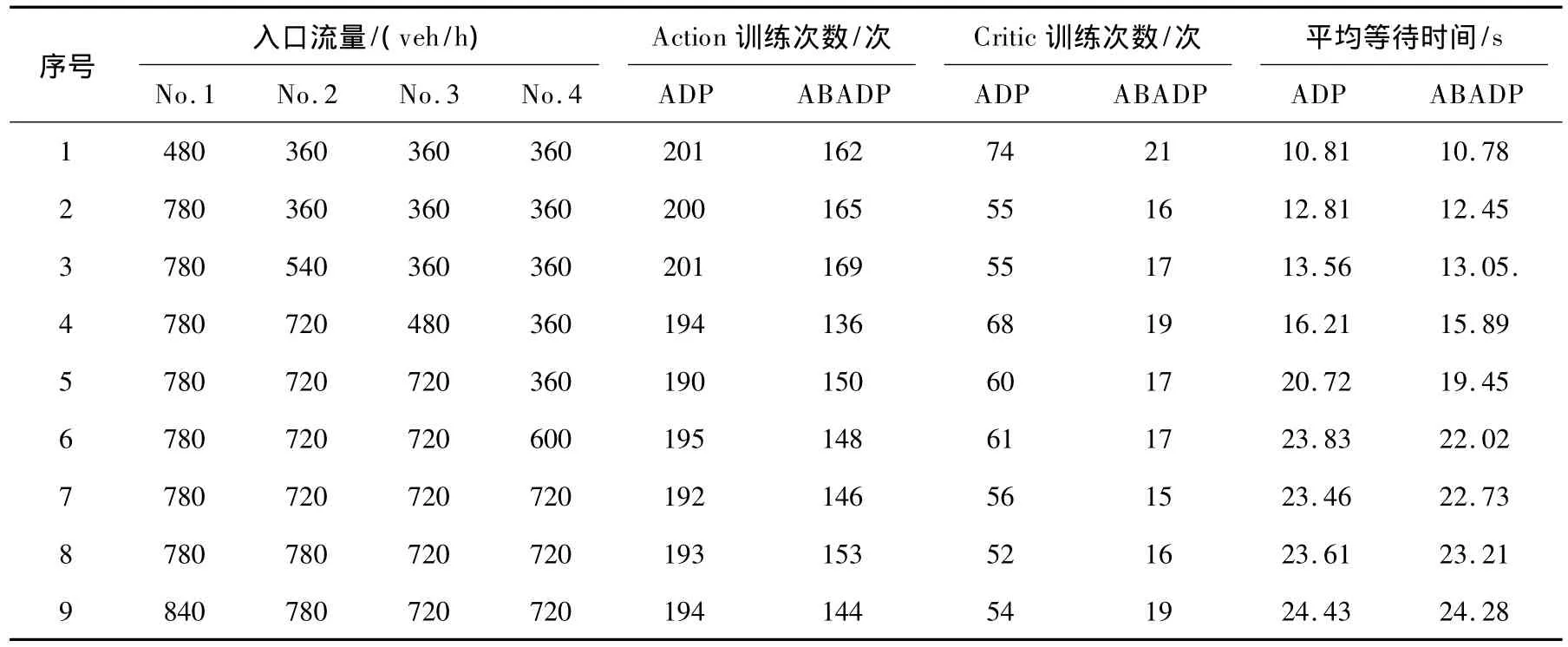
表2 ADP、ABADP控制速度仿真

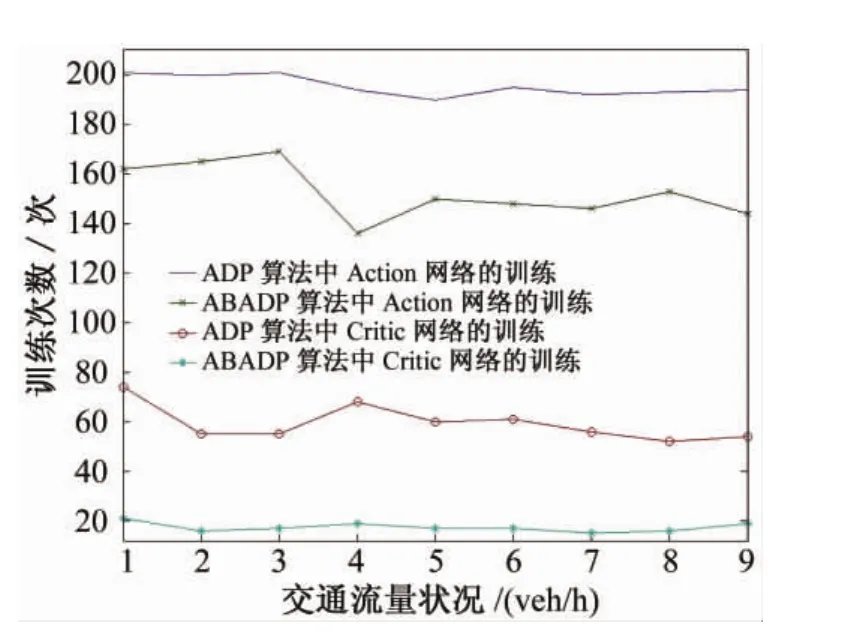
图7 ADP与ABADP算法训练次数比较

5 结论

本文针对传统ADP算法中Action模块和Critic模块所采用的梯度下降训练算法存在的一些缺点(如，局部极小点问题，必须知道所求解问题的微分信息等)，借用人工蜂群理论来训练传统ADP算法中的Action模块和Critic模块，加速ADP的学习速度。将人工蜂群理论用于ADP算法中Action网络和Critic网络的训练，给出相应的ABADP算法。该方法与梯度下降法不同，无需相应问题的导数信息，因此可用于不方便求解导数的问题，使所提出的ABADP算法的适用范围更广。仿真结果显示，将ABADP算法用于单交叉路口的交通信号控制中，控制性能得到了改进。

［1］于德新，高鹏，杨兆升．基于遗传神经网络的区域交通控制的效果评价［J］．北京工业大学学报，2010，36(4):490 －494．

［2］许卫明，潘国安．城市交通干线双向绿波带智能控制研究［J］．自动化博览，2008(S1):84－87．

［3］邱伟康，王伟智．基于模糊神经网络的交通信号控制［J］．江苏电器，2008(4):22－26．

［4］臧利林，贾磊，林忠琴．基于模糊逻辑的交通信号控制与仿真研究［J］．公路交通科技，2008，23(4):22 －26．

［5］赵冬斌，刘德荣，易建强．基于自适应动态规划的城市交通信号优化控制方法综述［J］．自动化学报，2009，35(6):666 －681．

［6］Khalid M，Liang S C，Yusof R．Control of a Complex Traffic Junction Using Fuzzy Inference［C］//5th Asian Control Conference，Melbourne:［s．n］，2004:1544 －1551．

［7］Colorni A，Droigo M，Maniezzo V．An Investigation of Some Properties of an Ant Algorithm［C］//In:Proc．of Parallel Problem Solving From Nature Conference(PPSN92)．Brussels:Elsevier Publishing，1992:509 －520．

［8］Eberhart R C，Kenney J．A New Optimizer Using Particles Swarm Theory［C］//Proc．Sixth International Symposium on Micro Machine and Human Science，Nagoya:［s．n］，1995:30 －43．

［9］李晓磊，邵之江，钱积新．一种基于动物自治体的寻优模式:鱼群算法［J］．系统工程理论与实践，2002，22(11):32 －38．

［10］Karaboga D．An Idea Based on Honey Bee Swarm for Numerical Optimization．Technical Report-TR06［R］．Erciyes University，Engineering Faculty:Computer Engineering Department，2005．

［11］Basturk B，Karaboga D．An Artificial Bee Colony(ABC)Algorithm for Numeric Function Optimization［C］//IEEE Swarm Intelligence Symposium，Indianapolis:［s．n］，2006:12 －14．

［12］Trabia M B，Kaseko M S，Murali A．A Two-stage Fuzzy Logic Controller for Traffic Signals［J］．Transportation Research，Part C，1999，7(10):353 －367．