静电场中高斯定理的证明

付 静， 姜广军

（吉林建筑工程学院城建学院 基础部，吉林 长春 130111）

0 引 言

高斯定理的证明一般有3种方法［1］：

1）利用电场线模型，先从点电荷位于球面内球心处的特例来证明高斯定理，然后再推广到任意的闭合曲面。这种方法相对比较简单，但是从特例推广一般情况不够严谨；

2）利用立体角的概念证明高斯定理，此方法虽严谨，但要求学生具有丰富的空间想象力，难度较大；

3）应用电场强度概念和纯数学推导证明高斯定理，这种方法非常繁杂和抽象，且物理含义不清晰。

1 电场强度通量的概念

借助于电场线的图像，引入电场强度通量的概念［2－4］。通过任意一曲面的电场强度通量如图1所示。

必须指出，对非闭合曲面，面法线的正方向可以取曲面的任一侧，对闭合曲面来说，通常规定自内向外的方向为面积元法线的正方向，所以，在电场线从曲面之内向外穿出处，E通量为正；反之，在电场线从外部穿入曲面处，E通量则为负。

图1

2 高斯定理的证明

2.1 正点电荷在球面中心

在正点电荷q激发的电场中，通过以点电荷为中心、半径为r的球面上的E通量如图2所示。

图2

利用库仑定律，在球面上任一点的电场强度为

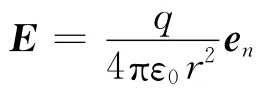
利用式（1）可求得通过该闭合球面上的E通量为：

2.2 正点电荷不在球面中心（或任意闭合曲面内）

图3

2.3 多个正点电荷在闭合曲面内

如图4所示，n个电荷在闭合曲面内，根据电场强度叠加原理，空间任一点的电场强度是这n个电荷电场的矢量和

此时，通过该闭合曲面的E通量是

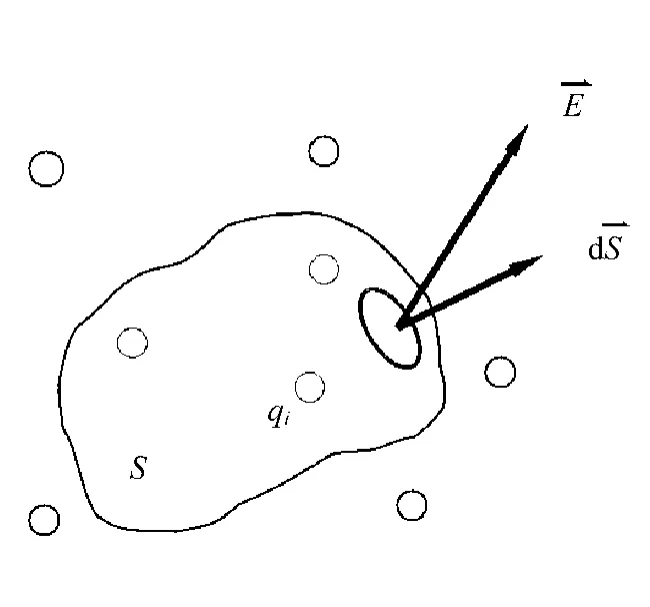
图4

2.4 正点电荷在球面外

如图5所示，如果闭合曲面内没有包围电荷，电荷在闭合曲面外面，那么进入闭合曲面的电场线等于穿出闭合曲面的电场线，所以总的E通量为0，即

综合以上讨论，不难得出结论，在静电场中，通过任一闭合曲面的E通量，等于该曲面内电荷量的代数和除以ε0，一般写为

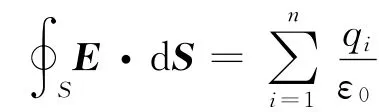
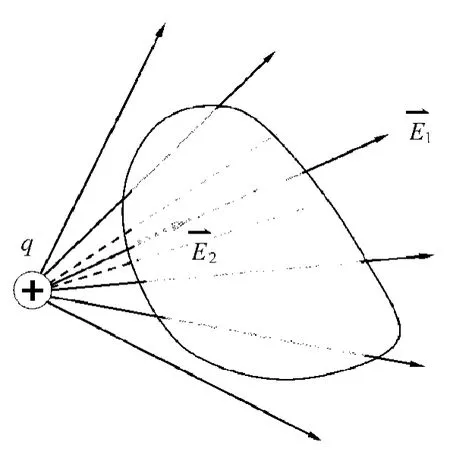
图5

3 对高斯定理的理解［5－7］

1）在等式左边的积分中，E是曲面S上各处的电场强度。闭合曲面即为高斯面。选取高斯面时，一般是根据对称性，使曲面的法线平行于该处的E，或使法线垂直于该处的E。

3）高斯面内以及面外的电荷位置的改变对高斯面上的通量没影响，但对高斯面上的电场强度是有影响的。

4）在实际应用中，高斯定理常用于电荷具有某种对称分布时所激发的对称的电场分布，即轴对称、球对称、面对称。

［1］高本领.高斯定理的简密推导［J］.高校理科研究，2009，34：90.

［2］赵凯华，陈熙谋.电磁学［M］.北京：高等教育出版社，2003.

［3］胡盘新，汤毓骏，钟季康.普通物理学简明教程［M］.2版.北京：高等教育出版社，2007.

［4］韦芙芽，张小林，叶爱华.高斯定理的直观教学［J］.电气电子教学学报，2009，31（2）：42－44.

［5］王先菊.高斯定理教学探讨［J］.考试，2010，18：182.

［6］沈晴，顾学文，徐筠，等.关于推证高斯定理不同方法的讨论［J］.物理通报，2011，40（9）：18－20.

［7］张清泽，陶宗明，陈宇.对高斯定理特性与应用的认识［J］.高等函授学报，2011，24（1）：29－30.

［8］付静，姜广军，袁明霞.普通物理学中磁场安培环路定理的证明［J］.长春工业大学学报：自然科学版，2012，33（6）：709－710.