基于关联度的代价敏感决策树生成方法

刘春英

0 引 言

决策树方法是数据挖掘中最常用的一种方法，它具有较好的分类预测能力，并能方便提取决策规则。决策树采用树形结构的表示方法，内部结点代表测试属性，分支代表测试属性的不同取值，叶节点代表分类的结果。在构建决策树的过程中，首先从所有测试属性中选择一个属性作为根节点，并根据此属性的不同取值划分成若干个分支，从上到下通过选择不同的测试属性递归构造决策树，直到叶子节点将测试样本划分为一类。常用的决策树生成方法有ID3方法［1］、C4.5方法［2］、CART 方法［3］、SLIQ 方法和 SPRINT［4］方法等。常用的决策树生成方法在选择属性分裂标准时以获得分类准确率为目标，没有考虑代价和自适应性问题。在追求分类准确率的前提下，综合考虑代价和自适应问题，提出了一种基于粗糙集的代价敏感决策树自适应生成方法。

1 相关概念和原理

定义1 决策表。

形式上，四元组I＝（U，R，V，f）是一个知识表达系统，其中U是对象的非空。U×R→V是一个信息函数，它为每个对象的每个属性赋予一个信息值，即有限集合，称为论域R是属性的非空有限集合。其中是属性r 的值域；f:∀r∈R，x∈U，f（x，r）∈V，一般简记为I＝（U，R）。如果R＝C∪D，其中C为条件属性集合，D为决策属性集合且C∩D＝／○，则这样的知识表达系统称为决策表。

定义2 等价类。

设I＝（U，R），P⊆R，则∩P也是一个等价关系，称为P上的不可区分关系，记为ind（P），ind（R）＝｛（x，y）∈U2｜∀a∈P，f（x，a）＝f（y，a）｝。由不可区分关系ind（P）产生的所有等价类用U／ind（P）表示，简记为U／P。

定义3 等价关系。

设I＝（U，R），P⊆R，X⊆U，P（X）＝｛x∈U｜［x］p⊆X｝和P（X）＝｛x∈U｜［x］p∩X≠／○｝称为X的P下近似和上近似。显然P（X）是根据知识P，U 中一定能和可能归入X 的元素的集合，P（X）是根据知识P，U 中一定能和可能归入X的元素的集合。posp（X）＝P（X）称为X是R 的正域。若P，Q是U 中的等价关系，posp（Q）＝

定义4 依赖度。

令I＝（U，R），P，Q⊆R，当设k＝γp（Q）＝时，称Q是k（0≤k≤1）度依赖于P。当k＝1时，称Q完全依赖于P；当0＜k＜1时，称Q部分依赖于P；k＝0时，称Q不依赖于P。其中，｜U｜表示U 的基数。

定义5 核与约简。

R中所有必要的属性组成的集合称为R的核，记作core（R）。如果∀r∈R都是必要的，则称R为独立的，否则称R为依赖的。设Q⊆R，如果信息系统I的一个约简。核与约简的关系为:core（R）＝∩red（R）。等式后边表示属性集的所有约简的交集。

定义6 关联度。

四元组I＝（U，R，V，f）是一个知识表达系统，其中R＝C∪D，C为条件属性集合，D为决策属性集合且C∩D≠／○，设VD｛dj｜j＝1，2，…，n｝为决策属性的取值序列，ci＝｛cij｜i＝1，2，…，m；j＝1，2，…，n｝为第i个条件属性的取值范围，决策属性D与条件属性ci的第cij个对象处的关联系数定义为:

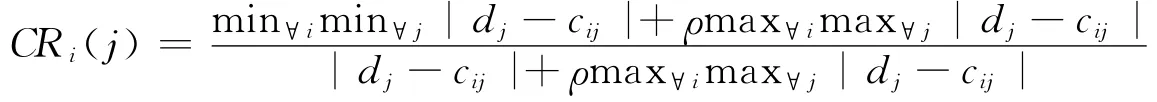
分辩参数ρ∈［0，1］。决策属性D与条件属性ci的关联度定义为:

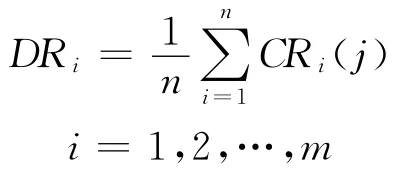
2 常用决策树生成方法和存在问题

2.1 常用决策树生成方法

Quinlan在1979年提出ID3方法是最典型的决策树生成算法，该方法以信息熵和信息增益度为分裂属性选择的衡量标准［5］。训练集S有m个类别，对应记录数为Si（i＝1，2，…，m），则集合S的信息熵的计算公式:

设测试属性A具有a1，a2，…，ax等x个不同的属性值，集合S被分成x个子集（S1，S2，…，Sx）。Sij代表Sj中包含类别Ci的记录数，则测试属性A的期望信息熵为:

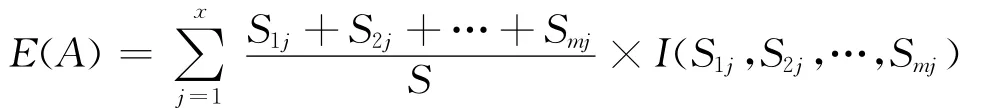
于是以测试属性A为分割点的信息增益为:

Gain（A）＝I（S1，S2，…，Sm）－E（A）

对ID3算法进行改进，1993年Quinlan提出的C4.5算法使用信息增益率作为分裂属性的选择标准，并且把连续属性值离散化，使C4.5能够对不完全数据进行处理。1976年B Kss博士提出卡方自动交互检测算法（CHAID），CHAID以每个分类变量的不同值建立多个分支，依据卡方分布的值决定是否对结点进行分裂，并且为缺失值单独建立分支［6］。1984年 Breman等提出CART算法选择GINI系数作为分裂属性的选择度量，对每个节点都进行二元分裂，所选择的分裂属性都以不纯度减少最大作为目标。1996年Mehta等 提 出 的 SLIQ（Supervised Learing In Quest）算法利用预排序技术和宽度优先策略，采用内存交换技术解决了数据量大于内存容量的问题［7］。

2.2 存在问题

决策树生成算法的关键问题在于如何选择分裂属性，不同的决策树生成算法采用不同的分裂属性选择方法。常用决策树生成算法具有理论清晰、计算便利等优点，但也存在以下不足:

1）没有考虑属性的关联度，分裂结点的选择偏向于取值较多的属性，而属性值较多的属性并不总是重要的属性。

2）没有考虑获取分裂属性所付出的代价。

3）没有考虑分裂属性所造成的误分类代价。

3 属性的关联度和属性约简

3.1 属性的关联度

四元组I＝（U，R，V，f）是一个知识表达系统，其中R＝C∪D，C＝｛ci｜i＝1，2，…，n｝为条件属性集合，ci＝｛cij｜j＝1，2，…，n｝，D 为决策属性集合且C∩D≠／○，决策属性D与条件属性ci的关联度为:

属性关联度DRi越大，说明条件属性对决策属性的影响程度越大，同时表明此条件属性所含有的信息量越大，对决策属性的重要程度越高。当大多数属性数据量较大、个别属性数据量较小时，常用决策树生成算法偏向于选择取值较多的属性，而属性值较多的属性并不总是重要的属性，从而掩盖了取值较少的属性的重要性。把属性的关联度引入作为选择属性的重要因素，以避免出现所选属性与现实无关或大数据量属性掩盖小数据量属性的错误。

3.2 属性约简

属性的重要程度并不相同，有些属性对分类结果并没有任何影响，故在决策树构建过程中要进行属性约简。属性约简是在整个知识表达系统分类能力不变的情况下，删除关联度小的和不重要的属性。属性约简首先从求核属性集合开始，在求核基础上依次顺序添加一个约简的属性，通过计算条件属性的关联度决定约简次序。

4 代价敏感学习

代 价 敏 感 学 习 （Cost-Sensitive Learning，CSL）最早在医疗诊断中被提出，医生在病情诊断过程中为病人的测试代价和期望得到的测试效果进行权衡。代价敏感学习定义为通过训练数据集训练出获得最小测试代价以及误分类代价的诊断学习系统［8］。因不同的属性值所获取的难易程度不同，代价敏感的决策树构建不只考虑分类的准确率，同时考虑属性的测试代价。代价敏感学习在构建决策树过程中，在误分类代价和测试代价之间权衡，优先选择具有最高性能价格比的属性作为分裂属性，其分裂属性选择标准与常用的决策树分类标准不同，存在很大的差别。属性的性价比是指误分类代价的减少值与其测试代价的比值，属性Ai的性价比cost＿ratio（Ai）定义为:

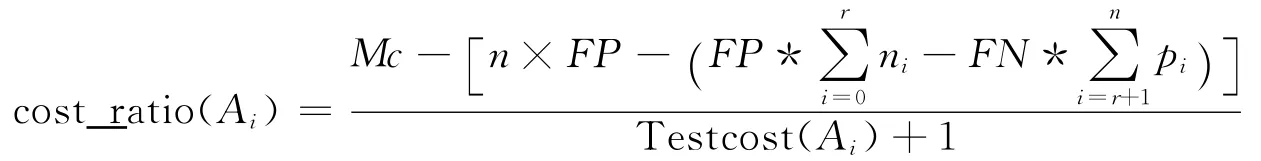
Testcost（Ai）代表属性Ai的测试代价，分母加1是为预防有的属性测试代价为0，导致分母为0的错误情况出现。分母代表选用属性Ai所带来的误分类代价的减少量，Mc代表没有选Ai作为分裂属性时的误分类代价。假设Ai有n个不同的属性值，则在分裂时可分成n个子结点（Node1，Node2，…，Noden），在这些子节点 Nodei中有pi个正例和ni个反例，设前r个子结点为正例结点，后（n－r）个为反例结点。

5 分裂属性的选择

在选择分裂属性时，要考虑分裂属性的关联度和属性的性价比，最优的结果是所选择的分裂结点属性关联度强并且性价比较高。要在属性重要度和性价比之间权衡，采用调和函数达到这个目的。对n个数据点x1，x2，…，xn的调和函数H（x）定义为:

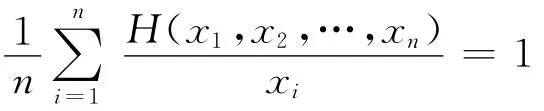
属性关联度DR（Ai）和性价比cost＿ratio（Ai）对应于调和函数的两个数据点，属性关联度和性价比的调和值:

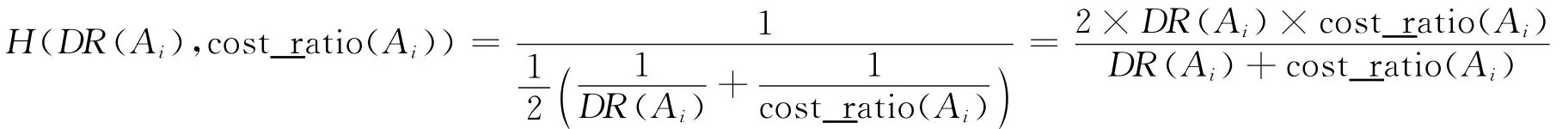
选用改进的信息增益作为分裂属性的选择公式，把属性关联度和性价比代入后信息增益公式改进为:

6 代价敏感决策树生成方法

6.1 条件属性约简方法

输入:四元组I＝（U，R，V，f）是一个决策表，其中R＝C∪D，C为条件属性集合，D为决策属性集合，且C∩D≠／○。

输出:决策表I的一个条件属性约简。

步骤1:计算条件属性C相对于决策属性D的相对核C0＝CoreD（C）。

步骤2:令B＝C0，对其余属性x∈（C－B），分别计算x与决策属性的关联度，并按照关联度由大到小的次序排列得X＝（x1，x2，…，xm）。

步骤3:依次按照关联度从大到小的次序把X中的属性xi加入B:B←B∪｛xi｝。若γB（D）＝γC（D），则执行步骤4，否则，反复执行步骤3，直到把X中所有属性都进行判断。

步骤4:算法结束，B∪D决策表I的一个属性约简。

6.2 代价敏感决策树生成算法

输入:四元组I＝（U，R，V，f）是一个知识表达系统，其中，R＝C∪D，C为条件属性集合，D为决策属性集合，且C∩D≠／○。

输出:代价敏感决策树。

步骤1:利用条件属性约简方法对C进行属性约减为C″。

步骤2:对约减后的条件属性集C″中的各个属性计算它的关联度。

步骤3:对约减后的条件属性集C″中的各个属性计算它的性价比。

步骤4:计算属性关联度和性价比的调和值H（DR（Ai），cost＿ratio（Ai））。

步骤5:以 H（DR（Ai），cost＿ratio（Ai））做分裂属性信息增益的参数，建立决策树。

步骤6:采用与C4.5相同的规则后修剪方法对生成决策树进行剪枝。

7 验 证

为了验证算法的有效性，取UCI中数据集中的数据进行试验，基于关联度的代价敏感决策树生成方法（CSDT）和常用决策树生成算法从分类准确率和生成决策树的结点总数进行比较。CSDT和常用决策树生成方法比较结果见表1。

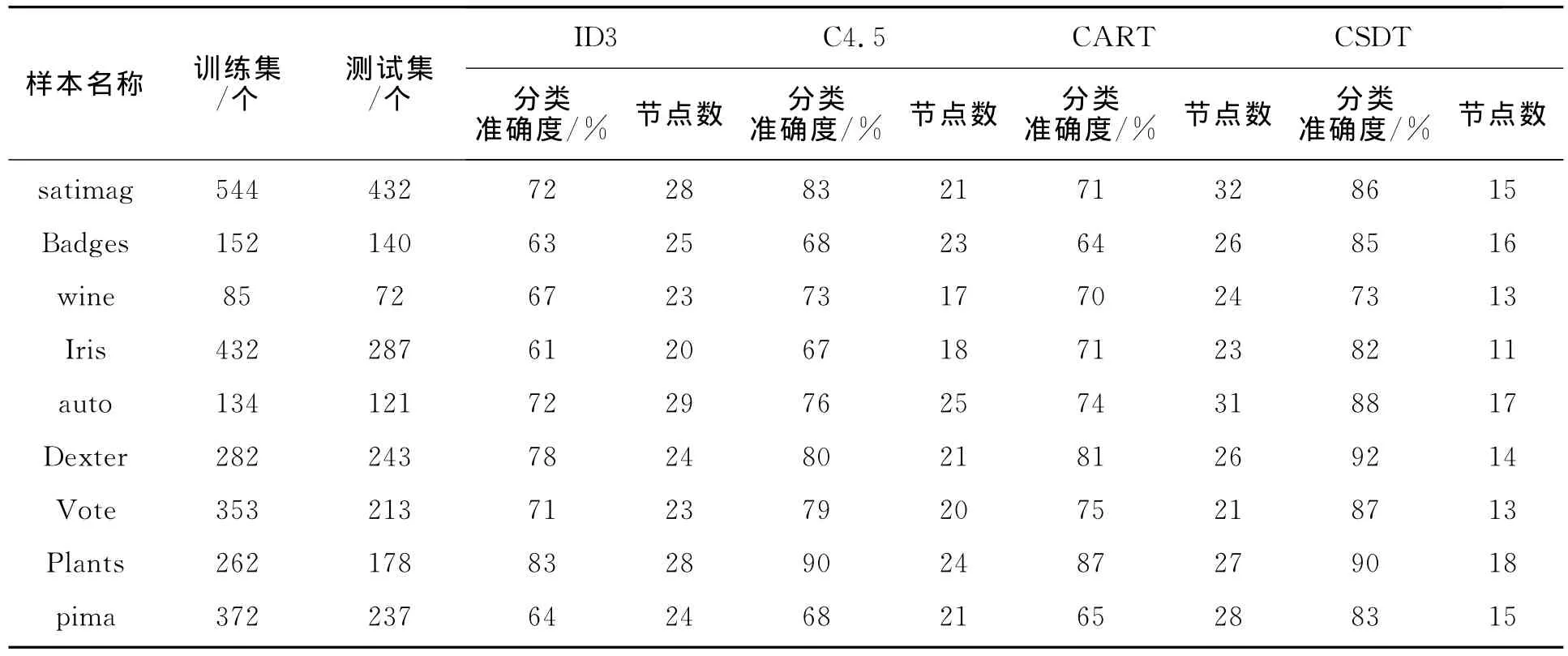
表1 CSDT和常用决策树比较结果

从表1中可以看出，基于关联度的代价敏感决策树生成的方法有较好的平均分类精确度，同时，构造的决策树有较低的复杂性。

8 结 语

把属性关联度和代价敏感思想相结合，提出了一种基于关联度的代价敏感决策树生成方法。该方法在选择分裂属性时不但考虑属性关联度，而且还结合了代价敏感的思想。实验结果证明，利用文中方法所构造的决策树具有较高的分类精度和较少的结点总数。

［1］ 朱颢东.ID3算法的改进和简化［J］.上海交通大学学报，2010，3（7）:53-57.

［2］ Quinlan J R.C4.5:Programs for machine learning［M］.San Mateo，CA:Morgan Kaufmann，1993:32-48.

［3］ 宋广玲，郝忠孝.一种基于CART的决策树改进算法［J］.哈尔滨理工大学学报，2009，4（2）:89-93.

［4］ Sharer J，Agrawal R，Mehta M.Sprint:A scalable parallel classifier of data mining［M］.San Francisco，CA:Morgan Kaufmann，1996:544-555.

［5］ 刘泽，潘晖.基于ID3算法汽车变速箱故障诊断系统［J］.长春工业大学学报:自然科学版，2011，32（6）:534-537.

［6］ 黄爱辉，陈湘涛.决策树ID3算法的改进［J］.计算机工程与科学，2009（6）:25-30.

［7］ 李世娟，马骥，白鹭.基于改进的ID3算法的决策树构建［J］.沈阳大学学报，2009（6）:45-49.

［8］ Turney P.Cost-sensitive classivication:Empirical evaluation of a hybrid genetic decision tree induction algorithm［J］.Journal of Artificial Intelligence Research，1995，2（3）:369-409.