电力系统强迫功率振荡过程中的功-能转换

黄 涌，云 雷，唐 飞，刘涤尘，孙文涛

（1.武汉大学 电气工程学院，湖北 武汉 430072；2.湖北省电力公司，湖北 武汉 430077；3.广东电网公司电力科学研究院，广东 广州 510600）

0 引言

随着跨区大电网的高速发展，实际系统中出现了一些由周期性扰动引起的强迫功率振荡现象[1-4]。其产生原因与振荡特征均不同于经典的负阻尼机理功率振荡[5-9]，因此强迫功率振荡受到了越来越多的关注[10-14]。 在振荡机理方面，文献[10]基于经典单机系统提出了电力系统强迫功率振荡的基础理论，文献[11]依据复模态分析方法分析了多机系统强迫功率振荡的稳态响应特性及主要影响因素，文献[12]分析了周期性负荷扰动引发强迫功率振荡的机理；在强迫振荡源方面，文献[13]分析了汽轮机功率扰动引起强迫功率振荡的共振机理，文献[14]利用系统中的能量转化特性识别强迫功率振荡扰动源位置。

电力系统是一个复杂的非线性系统，其本身具有一定的能量结构[15-19]，与弱阻尼自由振荡相比，电力系统强迫功率振荡具有完全不同的能量转换形式和特点。本文从电力系统强迫功率振荡过程中的功-能转换关系出发研究电力系统在强迫力作用下的能量变化情况，从功-能转换的角度分析系统强迫功率振荡机制及系统发生等幅振荡的原因。根据受迫振动机理[20]，当振荡源扰动频率不同时，系统的动能、势能及总平均能量均会呈现出不同的振荡幅度，与之对应的某振荡频率值会出现最大动能、最大势能和最大总平均能量的运行状态[21-23]，称之为动能共振、势能共振和能量共振状态，最后在前文分析的基础上研究了3种能量共振状态下系统的运行特性。

1 强迫功率振荡稳态响应

采用经典模型的单机无穷大系统，发电机采用二阶经典模型，根据受迫振动原理[20]，考虑发电机机械功率变化，将转子角运动方程在稳定运行点线性化之后可以得到：

其中，M为发电机惯性时间常数；DG为系统阻尼系数；K为发电机同步转矩系数；Δδ为转子角偏移量；ΔPm为机械功率变化量。

式（1）是一个二阶常系数非齐次微分方程，其解包括通解和特解2个部分[10]：通解即为所对应齐次微分方程的解，它只与系统本身参数有关，在一定时间内由于系统的阻尼作用逐渐衰减；而特解与发电机机械功率变化量ΔPm直接相关。本文将研究通解衰减以后系统特解的稳态响应特性。

假设机械功率为强迫振荡源，其变化量为ΔPm=F0cos ωnt，则式（1）可以写成：

其中，β=DG／（2M）为系统阻尼因子；为无阻尼自然振荡角频率；f0=F0／M，F0为振荡源波动幅值。

则系统的稳态响应及特解为：

相位φ随强迫振荡源频率ωn的变化关系见图1。

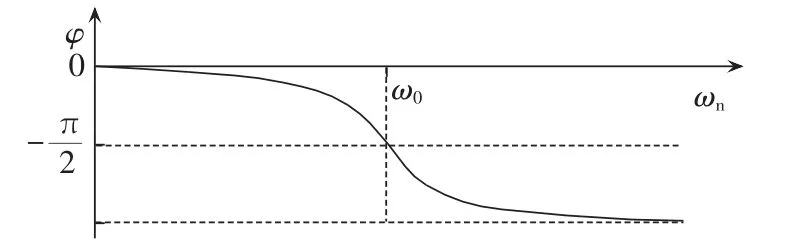
图1 相位φ随强迫源频率ωn的变化关系Fig.1 Curve of φ vs.ωn

发电机转子角速度变化量见式（4）。

2 系统的功-能关系

系统由于强迫力ΔPm的作用使转子角产生等幅振荡，则强迫力瞬时功率为：

功率振荡过程中，系统既受到强迫振荡源周期性外力的作用，还时刻受到发电机阻尼作用的影响而消耗系统能量，系统阻尼所消耗的瞬时功率为：

假设系统运行初态对应的时刻为t0，系统末态对应的时刻为t，则从初态到末态系统强迫力所做功WF和阻力做功WD分别为：

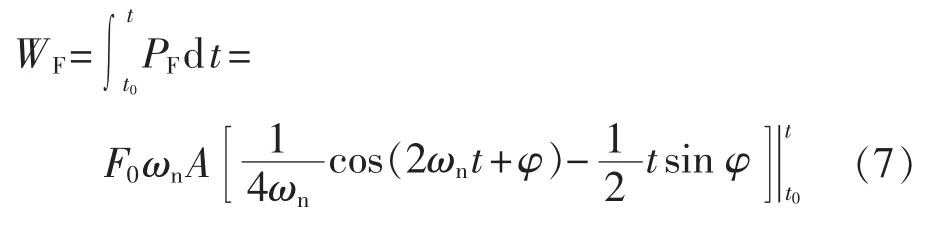
强迫力作用使系统转子角等幅振荡，从能量的角度来讲即是强迫力做功使系统的能量发生变化，因此可以将转子角的稳态响应特性描述为能量的变化量。

定义系统的动能为：

由式（9）可得动能与转子角的角速度直接相关。

系统的势能为：

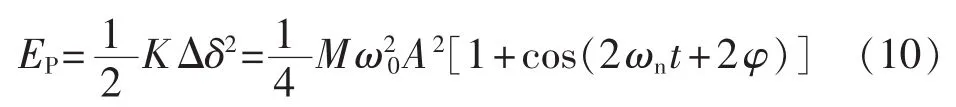
由式（10）可得势能与转子角偏移平衡位置直接相关。

系统在振荡过程中的瞬时总能量为：

系统动能和势能的维持是因为强迫振荡源作为强迫力向系统做功，同时因为系统本身的阻尼作用又从系统中消耗能量，两者之差即为系统总能量。从式（9）和式（10）可以看出系统动能和势能均随时间变化，系统总能量也以频率2ωn作周期性波动，说明强迫振荡过程中系统瞬时总能量不守恒，但是转子角却是在作频率不变的等幅振荡。

由式（12）和式（13）可以看出，强迫功率振荡过程中系统的动能、势能在每个周期内的平均值保持恒定，即周期时间内系统的总能量保持恒定，没有与外界的交换，但是动能平均值不等于势能平均值，其大小与强迫振荡源的频率有关。

3 强迫振荡过程中的功-能转换

以采用经典模型的单机无穷大系统为例分析不同情况下的系统功能转换。取参数M=12，DG=1，K=3（各参数均按标幺值计算），经计算系统无阻尼自然振荡角频率ωn=0.5 rad／s。

假设转子角从平衡位置到最大振幅处再回到平衡位置所对应的时间分别为t1、t2和t3。因为平衡位置时 Δδ=Acos（ωnt＋φ）=0，可得 ωnt＋φ=±π／2，又因为此时 Δω=ωnAcos（ωnt＋φ＋π／2）＞0，所以取ωnt＋φ=-π／2，可得 t1=（-π／2-φ）／ωn；转子角到最大位移处时，考虑到t2是在同一周期内到达最大幅值，对应 ωnt＋φ=0，可得 t2=-φ／ωn；再回到平衡位置时，ωnt＋φ=π／2，有 Δω=ωnAcos（ωnt＋φ＋π／2）＜0，可得 t3=（π／2-φ）／ωn。 因为-π＜φ＜0，所以需要将上述3个位置的时刻分别往后增加一个周期，最后可得 t1、t2和 t3如式（14）—（16）所示。

初始平衡位置时刻：

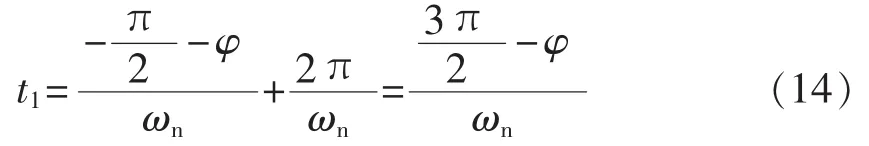
最大振幅时刻：

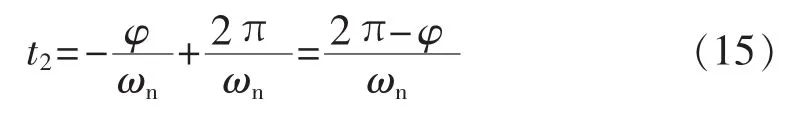
再次达到平衡位置时刻：

当转子角由平衡位置到最大振幅处时，将时刻t1、t2代入式（7）和式（8），可得：

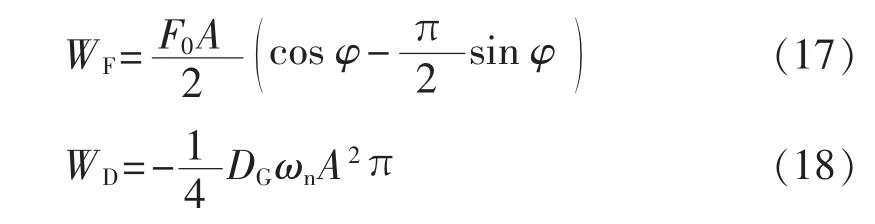
系统外力所做总功为：

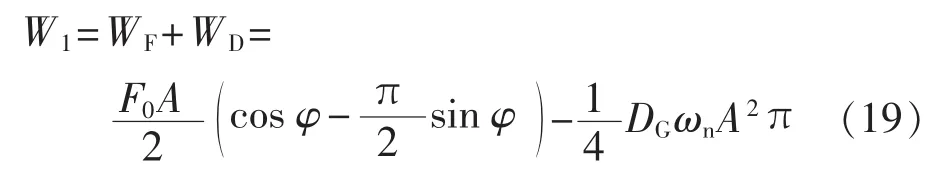
当转子角由最大幅值返回到平衡位置时，将时刻 t2、t3代入式（7）和式（8），可得：

系统外力所做总功为：

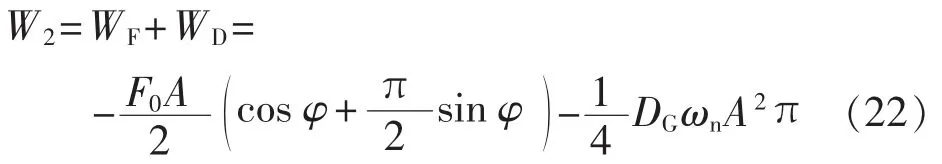
分别讨论强迫振荡源频率ωn不同时的系统功能转换。

3.1 ωn＜ω0的情况

根据图1，当ωn＜ω0时，相角φ位于第四象限，φ随着ωn的增大而减小。 当ωn由0ω0时，相角 φ 由0-π／2。 假设 ωn=0.4 rad／s，扰动幅值 F0=1.0，则强迫振荡源形式为 ΔPm=1.0cos（0.4t）。 通过式（14）、（15）和（16）可计算出 t1=12.67s、t2=16.59s、t3=20.52 s。将 t1、t2代入式（19），可得 W1=0.4071 p.u.，说明当转子角变化量由平衡位置到最大振幅时外力对系统做正功，转子角在此过程中吸收能量。又因为在t1时刻系统只有动能，而在t2时刻只有势能，所以系统在最大振幅处的势能大于在平衡位置的动能，即Epm＞Ekm（下标 m 表示最大值，后同）；将 t2、t3代入式（22），可得W2=-0.4071 p.u.，说明当转子角变化量从最大振幅回到平衡位置时，外力对系统做负功，系统向外界输出能量，故系统在t2时刻的势能大于t3时刻的动能，即Epm＞Ekm，可见转子角在前半个周期的波动过程中平均势能大于平均动能。转子角在后半个周期的能量转换与上述过程一致。系统转子角能量随时间变化曲线见图2，强迫力和阻力瞬时功率如图3所示。图2、3中纵轴所表示的量均为标幺值，后同。

图2 系统能量曲线Fig.2 Curves of system energy

图3 强迫力和阻尼功率曲线Fig.3 Curves of compelling force and damping power

由图2可见，系统势能幅值大于动能幅值，经计算可得，势能平均值，动能平均值，即，与分析结果一致。

3.2 ωn＞ω0的情况

同样根据图1，当ωn＞ω0时，相角φ位于第三象限，且φ随着ωn的增大而减小。当ωn由ω0∞时，相角 φ 由 -π／2-π。设 ωn=0.6 rad／s，扰动幅值F0=1.0，强迫振荡源形式为 ΔPm=1.0cos（0.6t）。 通过式（14）、（15）和（16）可计算出 t1=12.37 s、t2=14.99 s、t3=17.61 s。 将 t1、t2代入式（19），可得 W1=-0.3139 p.u.，说明当转子角变化量由平衡位置到最大振幅时外力对系统做负功，转子角在此过程中输出能量。在 t1时刻的动能大于t2时刻的势能，即Ekm＞Epm；将t2、t3代入式（22），可得 W2=0.3139 p.u.，说明当转子角变化量从最大振幅回到平衡位置时，外力对系统做正功，系统吸收能量，所以系统在t2时刻的势能小于t3时刻的动能，即Epm＜Ekm，转子角在前半个周期的波动过程中平均动能大于平均势能。转子角在后半个周期的能量转换与上述过程一致。系统转子角能量随时间变化曲线如图4所示，强迫力和阻力瞬时功率如图5所示。

由图4可见，系统动能幅值大于势能幅值，经计算可得，势能平均值，动能平均值，即，与分析结果一致。

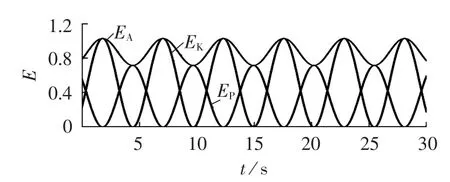
图4 系统能量曲线Fig.4 Curves of system energy

图5 强迫力和阻尼功率曲线Fig.5 Curves of compelling force anddamping power

由3.1节、3.2节，从t1到t3时刻，系统外力所做总功为W1＋W2=0，同理，在转子角变化量的后半个周期外力做功同样为0，即周期内转子角的总能量总是保持不变，强迫力对系统所做的功正好等于系统阻力所消耗的能量，系统正是在这种能量的吸收和耗散过程中保持等幅振荡。所不同的是系统动能和势能对能量的吸收程度的不同，表现为其平均值的大小关系，而这依赖于强迫振荡源的频率。

3.3 ωn=ω0的情况

当强迫振荡源频率ωn=ω0时，由图1可知相角φ=-π／2，将相角 φ 代入到式（5）和式（6）可得：

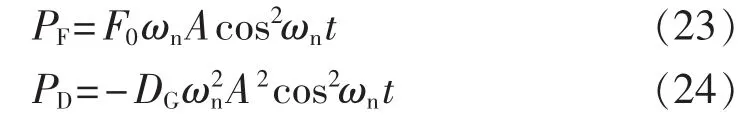
根据第1节中系统的稳态响应特性，将式（23）和式（24）化简可得：

式（25）表明，在系统强迫振荡的任何时刻，外力对系统做功始终为0（如图6所示），这是强迫振荡的特殊情况，即经过任意时间段，系统的总能量时刻保持恒定，与外界没有能量交换，能量只在动能和势能之间转换（如图7所示），两者之和恒为定值。此时系统可以称为达到能量吸收和消耗的最佳状态。

同样根据式（14）、（15）和（16）可计算出 t1=12.56 s、t2=15.70 s、t3=18.84 s。 计算 t1到 t2时刻的外力做功W1=0，t2到t3时刻的外力做功W2=0，系统总能量保持恒定。同时可以求出势能平均值，动能平均值，即。

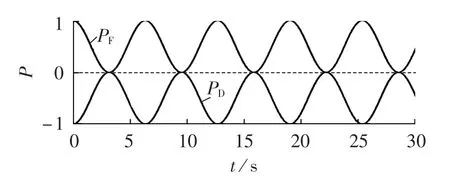
图6 强迫力和阻尼功率曲线Fig.6 Curves of compelling force and damping energy

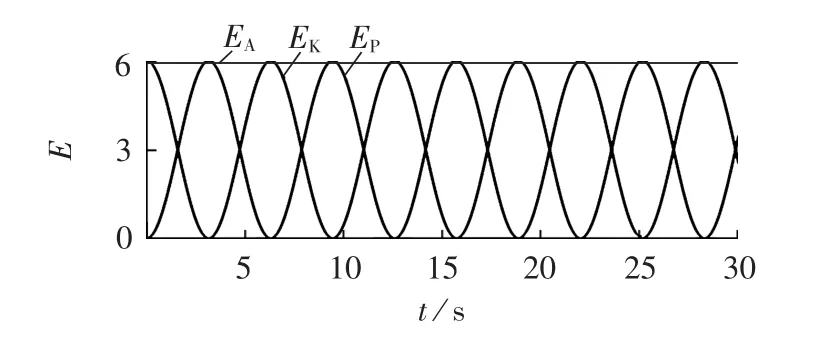
图7 系统能量曲线Fig.7 Curves of system energy

4 能量共振

如前文所述，当振荡源频率ωn=ω0=0.50 rad／s时，系统的能量时刻保持恒定，根据式（4）中转子角振幅求极值可知，此时系统的速度振幅达到极大值，称之为动能共振状态。式（5）和（6）还说明：强迫力做功即系统吸收的功率与转子角速度成正比，而阻尼消耗功率却与角速度平方成正比，阻尼消耗功率增长速度大于系统吸收功率的增长速度，说明角速度振幅对维持系统等幅振荡起了关键性作用，所以在ωn=ω0时，系统从强迫振荡源吸收功率达到最佳状态，这就要求角速度有相应的最大值，才能使阻尼消耗功率与强迫力做功相抵消。

动能共振状态下系统的总能量似乎达到一个比较大的运行状态。但是根据式（11）可以看出系统总能量直接依赖于转子角速度和振动位移，而对应能量的稳态响应和强迫力直接相关。总能量平均值必定对应振荡源某一频率处达到最大值，称此时系统处于能量共振状态。

系统总能量平均值为：

根据式（26），应用求极值的微分判据，对总平均能量求导，可以求出系统发生能量共振的条件为：

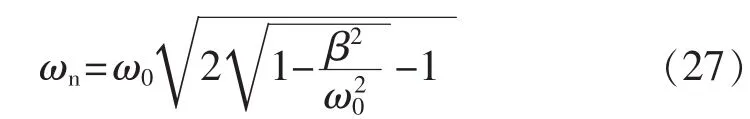
式（27）可进一步简化为：

式（26）—（28）表明系统发生能量共振时的振荡源频率ωn＜ω0，这属于第3.1节中的情况，说明当ωn=ω0并不是系统平均能量最大的条件。

在此条件下，系统平均能量的最大值为：

以上2种能量共振分别对应着系统的最大动能和最大总能量，但是对于电力系统而言，发电机转子角的振荡幅度无疑才是对电网安全稳定影响最为显著的因素，因此对式（3）转子角位移的振荡幅度求极值，可得当时，系统转子角位移达到最大值，此时系统处于势能共振状态。

如前文所述，系统在发生强迫功率振荡时，由于能量在每周期内的平均值相等，系统在每个周期内与外界交换的能量平均值为0，强迫力做功仅用于补偿阻尼消耗能量。由于系统的能量直接依赖于转子角位移和角速度，而角速度又直接与功率损耗和吸收有关，所以系统能量与强迫力之间有着必然的联系。但是，系统能量吸收和消耗的最佳状态并不是系统总能量达最大的状态，既然系统总能量直接依赖于转子角位移和角速度，所以可以判断系统的总平均能量最大值发生在系统动能共振和势能共振状态之间，这与本节中各能量共振状态对应的振荡源频率计算结果是一致的。

5 结论

本文研究了电力系统强迫功率振荡过程中的能量共振，用功-能转换来描述系统强迫振荡运行状态。

a.强迫振荡过程中转子角的势能和动能均随时间作周期性波动，但两者在每个周期内的平均值均保持恒定，系统总能量平均值在一个周期内亦保持不变。

b.转子角变化量从平衡位置到最大位移处再回到平衡位置时，外力对系统做功为零，说明强迫力对系统做的功用于补偿系统阻尼消耗功率，同时也解释了系统总能量平均值保持恒定的原因。

c.分析了系统对应不同振荡源频率时的动能共振、势能共振和总能量共振状态，验证了系统能量与转子角位移和角速度之间的关系，最后分析了系统发生总平均能量共振的条件。