基于小生境遗传算法的微电网控制与优化

王瑞琪，张承慧，李 珂，陈阿莲，杜春水

（1.山东大学 控制科学与工程学院，山东 济南 250061；2.山东大学 电力电子节能技术与装备教育部工程中心，山东 济南 250061）

0 引言

微电网作为一种能量供应系统中增加可再生能源和分布式能源渗透率的新型能量传输模式和组织形式，成为国内外研究的重点[1-2]。微电网由分布式电源（DG）、储能装置、能量变换装置、相关负载和监控、保护装置汇集而成，能够有效提高电力系统运行的灵活性、高效性和清洁性，更好地满足电力用户对电能质量、供电可靠性的要求[3-4]。微电网存在2种典型的运行模式：在正常情况下，微电网与主电网并联运行，称为并网运行模式；当检测到电网故障或者电能质量不满足要求时，微电网将及时与主电网断开而处于独立运行模式。微电网同时需要根据实际运行状况在2种模式之间切换运行。

无论是并网运行还是独立运行，在维持电压幅值和频率稳定的同时实现功率的快速准确分配，以及在模式切换过程中保证扰动振荡在可接受的范围之内，是微电网控制问题的难点和重点。文献[5]提出了一种针对微电网不同运行模式对DG采用不同控制策略的思想，并网运行时DG采用PQ控制，独立运行时采用U／f控制，但这种方法会在运行模式切换时产生暂态振荡。文献[6]根据微电网内不同的DG单元采用不同的控制策略，对电能输出稳定的DG采用U／f控制策略，对受外部条件影响较大的DG采用PQ控制，改善了微电网运行特性，但降低了系统运行的灵活性和稳定性。

另一方面，微电网在不同工作模式下以及模式切换过程中的稳态和暂态性能与控制参数密切相关。文献[7-10]分别通过频域特性和小信号动态模型分析了控制参数对微电网运行特性的影响，但是只能得到控制参数的大致范围。文献[11]采用粒子群算法优化微电网小信号模型的方法获取控制参数的最优值，但是小信号模型本质上依赖于具体的稳态运行点且无法考虑动态切换过程。

本文提出了一种包含改进动态特性的功率分配控制器、带前馈补偿的电压电流双闭环控制器的微电网控制策略，并基于小生境遗传算法优化微电网的运行特性。基于微电网的小信号动态模型，分析了影响微电网运行特性的主要控制参数及其优化取值域。为提高优化目标函数的精确性，采用专业暂态仿真软件PSCAD／EMTDC搭建了微电网时域仿真模型，并进行了微电网各种运行状态及模式切换的仿真，保证了控制策略在多种工作模式下的鲁棒性能。基于小生境遗传算法对所提微电网控制策略的主要参数进行了优化设计，提高了微电网在不同运行模式下以及模式切换过程中的稳态特性和动态性能。

1 微电网结构

在典型的微电网结构中，风力发电机、光伏电池、燃料电池等DG通过电力电子变换装置转换后，经逆变器并入微电网。微电网通过静态切换开关在公共连接点（PCC）处与主网相连。本文所采用的微电网系统等效电路如图1所示，DG1与负载之间部分由LC滤波器电感Lf1、电容Cf1、耦合电感LC1及寄生电阻Rf1、RC1组成。Load1和Load2为本地负荷，Load3 为公共负荷，Rn1、Rn2、Ln1、Ln2为线路电阻与电感。文中DG1和DG2均假设为直流源或整流后的直流源。对于出力具有不稳定性和间歇性的能源如风能、太阳能，DG在其整流后的直流母线侧通过双向DC-DC变换器并联储能装置[12-13]，可以平抑功率波动，维持直流母线电压稳定，亦适用于本文方法。

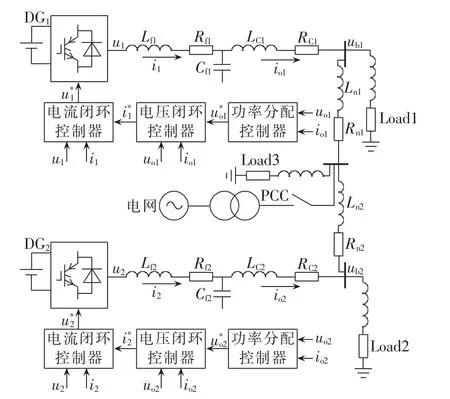
图1 微电网系统等效电路及控制结构图Fig.1 Equivalent circuit of microgrid and control structure

2 微电网控制策略

微电网的控制结构如图1所示，无论是处于并网运行还是孤岛运行模式，DG都可以通过功率分配控制器实现功率共享，产生闭环控制的参考电压。带前馈补偿的电压电流双闭环控制保证了逆变器输出电压和输出电流的快速调节和无差跟踪。

功率分配控制器基于改进动态性能的下垂控制特性，其控制结构如图2所示。

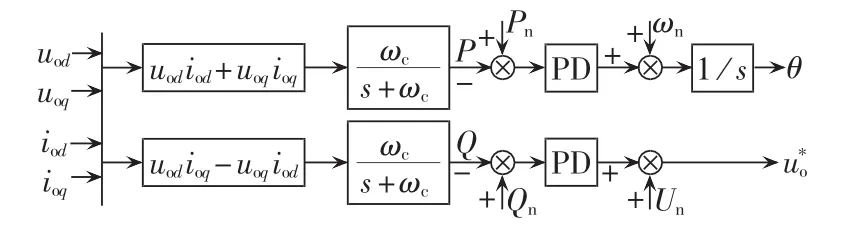
图2 功率分配控制器框图Fig.2 Block diagram of power allocation controller

平均功率P、Q由瞬时输出电压和电流计算后经低通滤波器得到：

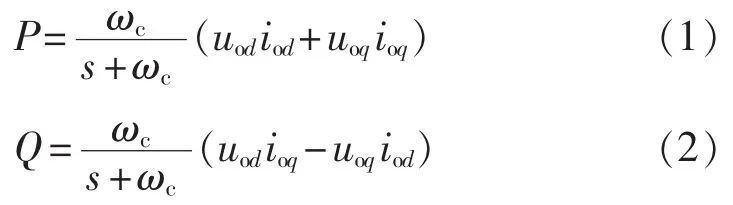
其中，ωc为低通滤波器的截止频率；uod、uoq、iod、ioq分别为输出电压和电流的d、q轴分量。

为提高系统动态性能，基于改进下垂特性的功率调节关系为：

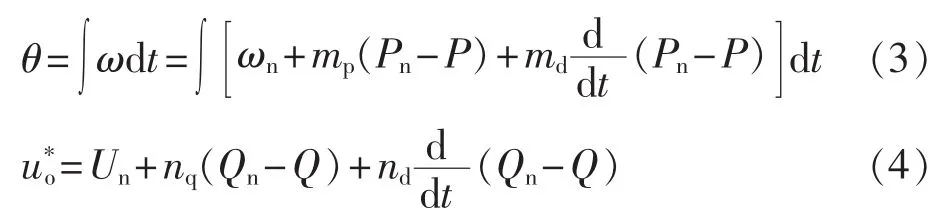
其中，ω和θ分别为DG所在dq旋转坐标系的旋转角频率和相角；ωn、Un分别为额定角频率和电压幅值；Pn、Qn分别为DG的额定有功和无功功率，一般取Pn为逆变器的额定有功功率，Qn=0；mp、nq为下垂增益，md、nd为暂态增益。

由式（3）、（4）及图 2 可见，功率分配控制器可等效为比例微分（PD）控制器，mp、nq可有效实现功率分配及电压幅值和频率调节；md、nd对不同运行状态下的振荡起阻尼作用，提高系统的动态性能。因此，微电网在孤岛运行时，DG基于改进的下垂特性实现功率共享并承担电压和频率的调节作用；并网运行时，微电网由主电网提供电压和频率的支撑，功率分配控制器等效为PQ控制方式使DG输出给定功率。无论微电网处于并网还是孤岛运行模式，都可以通过功率分配控制器实现DG之间的负荷分配，无需控制策略切换，降低了暂态振荡的可能性。

为稳定负载电压，提高系统的动态响应，采用带前馈补偿的电压电流双闭环控制器，其结构见图3。

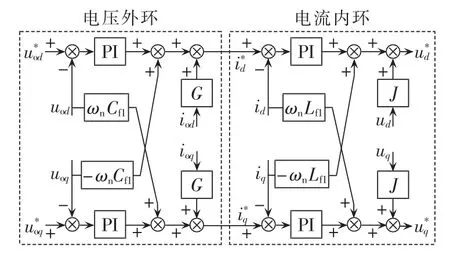
图3 电压电流双闭环控制框图Fig.3 Block diagram of voltage and current dual close loop control

电压外环控制的动态特性为：

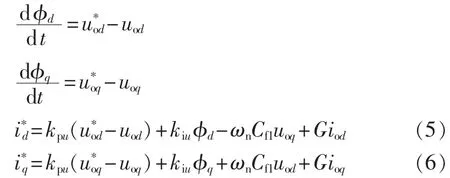
其中，kpu、kiu分别为电压PI控制器的比例和积分系数；φd、φq为电压比较的积分量；G为前馈增益。

电流内环控制的动态特性为：

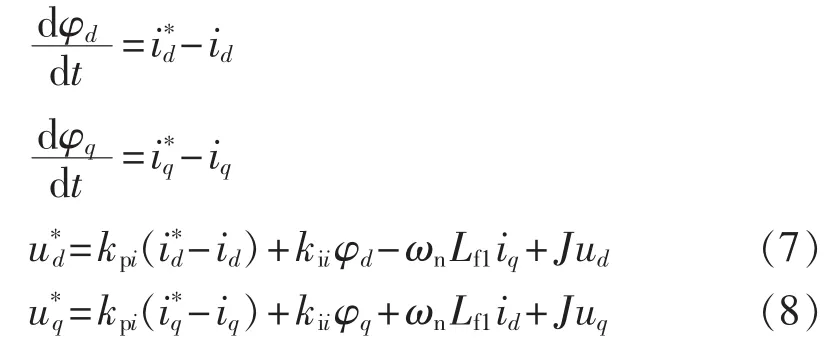
其中，ud、uq、id、iq分别为逆变器d、q 轴的电压和电流；kpi、kii分别为电流PI控制器的比例和积分系数；φd、φq为电流比较的积分量；J为前馈增益。

3 微电网小信号动态建模与分析

3.1 微电网的小信号动态建模

为了分析微电网的内在运行机理以及控制参数对微电网运行特性的影响，建立如图1所示的微电网电路及控制结构的小信号动态模型。

每个DG的逆变器模型建立在其输出电压确定的旋转角频率为ωi的dq旋转坐标系上，为建立整个微电网的动态模型，需要将DG模型变换到旋转角频率为ωcom的微电网全局参考坐标系下[14]，则第i个DG的逆变器参考坐标系与微电网全局参考坐标系的夹角为：

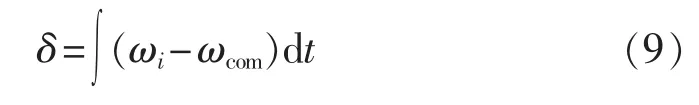
DG1接口电路的电压、电流动态特性可以表示为：

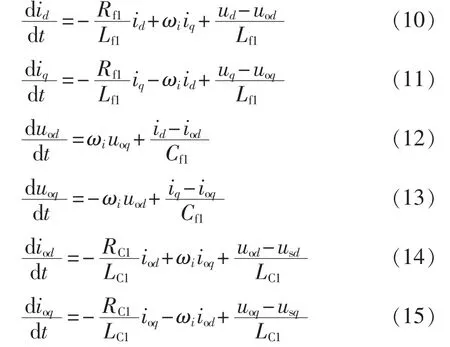
其中，usd、usq分别为d、q轴的交流母线电压。

式（1）—（15）描述了微电网中DG的动态特性，将其在稳态运行点处线性化可得：

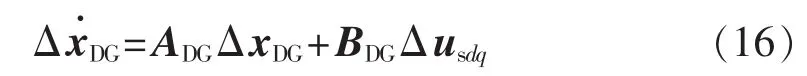
其中，ΔxDG=[Δδ ΔP ΔQ ΔφdqΔφdqΔidqΔuodqΔiodq]T；ADG、BDG分别为状态矩阵和输入矩阵；Δusdq=[ΔusdΔusq]T，文中所有下标为dq的变量均为类似列向量。

ADG、BDG为：

其中，ω1为 DG1的旋转角频率，Id、Iq、Iod、Ioq分别为 id、iq、iod、ioq的稳态值，Uod、Uoq、Usd、Usq分别为 uod、uoq、usd、usq的稳态值。

整个微电网的小信号动态模型包括：DG的小信号动态子模型和网络及负载小信号动态子模型。类似于DG的接口电路模型，网络及负载小信号模型由网络及负载的电路等效微分方程线性化后得到[15]。通过坐标变换将各DG的小信号模型和网络及负载小信号模型变换到全局参考坐标系下，得到整个微电网的小信号状态空间模型：

其中，A、B分别为微电网的状态矩阵和输入矩阵，Δx、Δu分别为包含DG、线路和负载状态变量的微电网状态矢量和输入矢量。

3.2 小信号动态分析

根据经典控制理论，小信号模型的特征根反映了系统的稳定性、动态性能和阻尼特性，而且系统的频率模式与特征根也密切相关[16-17]。微电网小信号模型的所有特征根分布如图4所示，在较宽的频带内，系统的特征根被明显地分为高频（约1.6 kHz）、中频（400～650 Hz）、低频（2～10 Hz）3 组频率模式。 根据敏感度分析理论，特定的特征根针对某频率模式的敏感度很强，而对其他频率模式的敏感度可以忽略不计。例如高频模式对应于电流控制闭环和滤波电路；中频模式对电压控制闭环的特征根较为敏感；功率分配控制器处于低频模式。这种频率模式分布特征避免了外层控制闭环对内层控制闭环稳定性和鲁棒性的影响，保证了微电网的良好运行，同时为单独整定不同频率模式下的控制器参数提供了理论基础。功率控制器的特征向量对应于低频模式下的主导极点，对微电网运行的稳定性和动态性能的影响起主导作用。因此，功率控制器的下垂增益mp、nq和暂态增益md、nd的优化设计，可以有效提高微电网系统的运行特性。

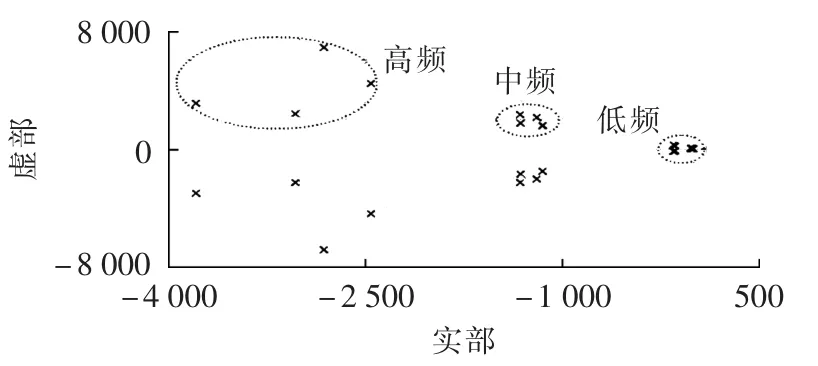
图4 微电网的特征根分布Fig.4 Eigenvalue distribution of microgrid

图5（a）为 5×10-6≤mp≤3×10-4且 md=0、10-6、5×10-6、10-5、2×10-5时，功率控制器的特征根 λ1、λ2、λ3的变化轨迹，其中实线箭头表示mp增加时特征根的变化方向，虚线箭头表示md增加时根轨迹簇的变化方向。当mp较小时，系统的一对共轭复根λ2、λ3距虚轴较远，接近虚轴的实根λ1为主导极点，系统可以等价为一阶系统。此时系统无超调，但是存在稳态误差且动态响应慢。随着mp的增加，实根λ1逐渐远离虚轴而共轭复根λ2、λ3逐渐接近虚轴成为主导极点，系统近似为二阶系统，动态响应性能提高。同时，共轭复根λ2、λ3也逐渐远离实轴，系统有超调且存在振荡，振荡幅值越来越大。当加入暂态环节时，随着md的增大，特征根 λ1、λ2、λ3与虚轴的距离越来越大，因此系统的动态响应越来越快，验证了本文采用的功率控制器能够有效提高微电网的动态性能。图5（b）为 5×10-6≤mp≤3×10-4且 nq=10-4、5×10-4、10-3、2×10-3、3 × 10-3时，功率控制器的特征根 λ1、λ2、λ3的变化轨迹，其中实线箭头表示mp增加时特征根的变化方向，虚线箭头表示nq增加时根轨迹簇的变化方向。从图中可以看出，不断增加nq，会使系统共轭复根λ2、λ3落在虚轴的右侧，此时系统不稳定。

根据上述分析可知，功率控制器参数的匹配选择决定了微电网系统的稳定性和动态性能，同时不同参数对系统稳定性和动态性能的影响不同，且参数间也存在耦合作用。 图 6（a）和（b）分别为 0≤md≤2×10-5和 5×10-6≤mp≤3×10-4时的根轨迹在 nd取不同值时形成的曲线簇，其中实线箭头分别表示md、mp增加时特征根的变化方向，虚线箭头表示nd增加时根轨迹簇的变化方向。

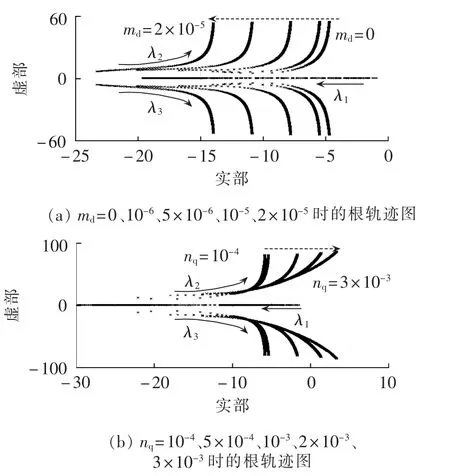
图5 mp变化时的根轨迹图（5×10-6≤mp≤3×10-4）Fig.5 Root locus diagram for mp change（5×10-6≤mp≤3×10-4）

图6 nd取 0、5×10-6、10-5、3×10-5时的根轨迹图Fig.6 Root locus diagram for nd=0，5×10-6，10-5，3×10-5

综合考虑微电网系统的稳态性能和动态特性，基于小信号动态分析理论设计参数 mp、md、nq、nd的优化取值域，可以有效提高优化效率，大幅降低计算成本，保证综合优化目标的实现。表1为经过小信号动态分析之后的参数优化取值域。在复平面上对应于参数优化取值域的特征根区域如图7所示，其兼顾了微电网系统的稳定性和动态性能。

表1 参数优化取值域Tab.1 Optimization range of parameters

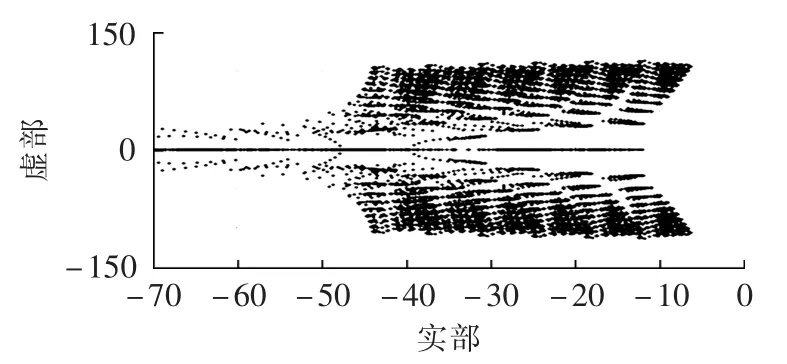
图7 参数优化取值域的特征根区域图Fig.7 Root area diagram of optimization range of parameters

4 基于小生境遗传算法的微电网运行优化

4.1 目标函数

微电网运行涉及多种工作模式：并网运行模式、并网与独立运行模式的切换、负荷突变的独立运行模式、重新并网运行模式。为了使微电网实现多种工作模式的稳定运行和平滑切换，稳定高效地控制DG输出，同时使系统电压幅值和频率较快地稳定在额定值附近，建立了微电网运行优化的目标函数：

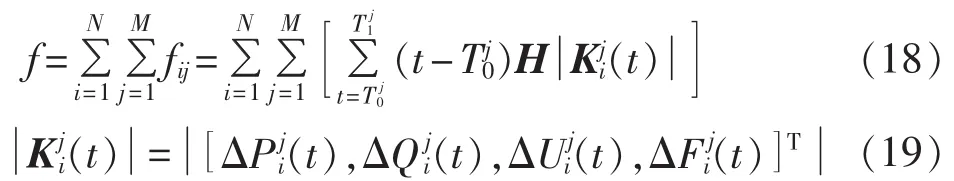
其中，N和M分别为微电网的DG数量和工作模式数量，N=2，M=4；t为仿真时间；T0j、T1j分别为工作模式j下的计算开始与终止时间；H为权值矩阵，H=[1，1，10，20]；为t时刻第i个DG在工作模式j下的绝对误差矩阵，ΔPji（t）和 ΔQji（t）分别为 t时刻采样的第i个DG在工作模式j下的有功功率和无功功率控制误差；ΔUij（t）和 ΔFij（t）分别为 t时刻采样的第i个DG在工作模式j下的电压幅值和频率与额定值的偏差。需要指出的是，计算目标函数的采样数据均转化为标幺值。

目标函数的计算需要不断采样t时刻的有功功率、无功功率、输出电压幅值和频率等数据，因此采样数据的准确性决定了微电网运行优化结果的实用性和有效性。电力系统暂态仿真软件PSCAD／EMTDC能够有效逼近真实的电力系统稳态和暂态过程，在国际电力系统分析领域得到了广泛应用和认可[18-19]。为了实现目标函数的准确建模，本文利用PSCAD／EMTDC软件建立了如图1所示的微电网模型并进行微电网多种工作模式及模式切换的非线性时域仿真。利用PSCAD／EMTDC与MATLAB的数据接口，基于MATLAB的强大计算能力和可视化技术进行了优化算法编程和数据处理。

4.2 基于小生境遗传算法的微电网运行优化

微电网的运行优化是具有约束域的非线性优化问题，其优化变量[mp，md，nq，nd]之间存在复杂的耦合作用且目标函数不可微，故常规的数学优化方法并不适用。遗传算法是一种模拟生物遗传和进化过程的现代启发式算法，具有高度并行、随机、全局搜索以及自适应等特点，非常适合复杂非线性优化问题的求解。但遗传算法容易发生非全局性收敛或收敛速度缓慢等问题，主要表现在种群中所有个体都趋于同一状态时停止进化，从而收敛于局部最优解。

本文采用小生境技术[20]和自适应技术[21]改进传统遗传算法。小生境技术采用海明距离作为共享函数，当遗传算法种群中的2个个体Xi和Xj之间的海明距离小于预先指定的某一距离L时，比较个体Xi和Xj的适应度大小，并对其中适应度较低的个体处以惩罚函数。这样，较差的个体在后面的进化过程中被淘汰的概率极大，即在距离L之内只存在1个优良个体，从而既维护了种群的多样性，又使得个体能够在整个优化取值域中分散开来，避免陷入局部最优。同时，采用自适应概率算术交叉与变异运算，根据进化过程自适应调整算术交叉和变异的概率，有效提高小生境遗传算法的寻优效率和收敛速度。

本文以微电网控制参数为优化变量X=[mp，md，nq，nd]，综合利用 PSCAD／EMTDC 与 MATLAB 软件，基于小生境遗传算法优化微电网运行的流程如图8所示，其中无阴影图框表示MATLAB环境下的进程，有阴影图框表示PSCAD／EMTDC环境下的进程。

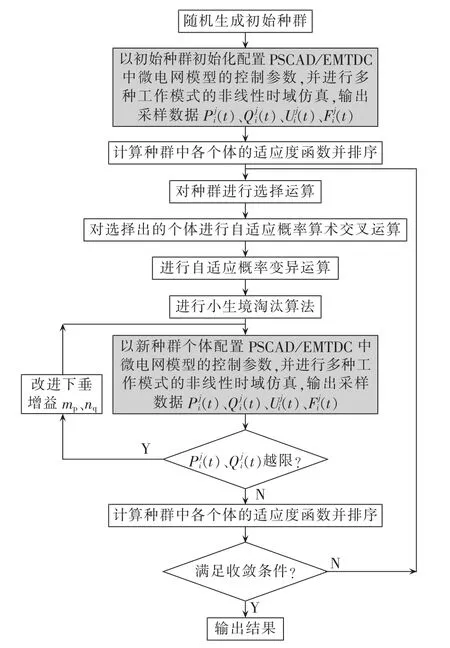
图8 微电网运行优化的流程图Fig.8 Flowchart of microgrid operation optimization

需要说明的是，在实际微电网运行中，算法优化结果可能会超出DG出力的限制，造成系统的电压幅值和频率不符合 IEEE Std 1547.4—2011[22]标准要求，严重时会导致系统失稳。因此，在循环周期内根据PSCAD／EMTDC下的微电网仿真结果对下垂增益进行改进：

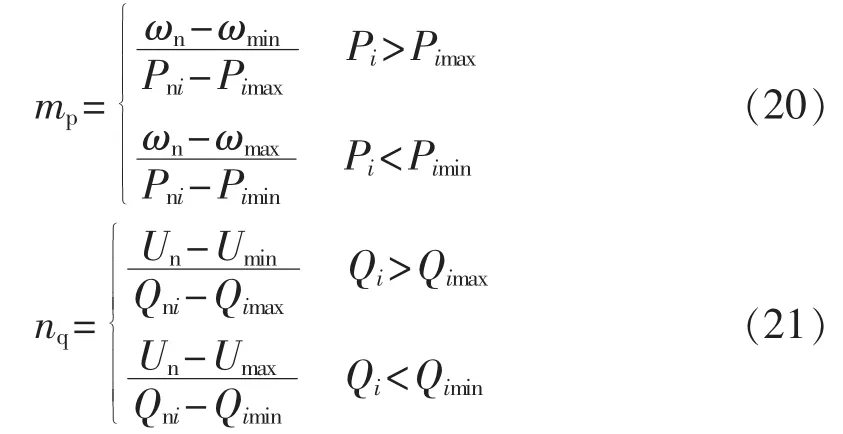
其中，Pi、Qi、Pni、Qni分别为微电网中第 i个 DG 的实际输出功率和额定功率；Pimax、Qimax、Pimin、Qimin分别为微电网中第i个DG输出有功功率和无功功率的上限和下限；微电网的电压频率和幅值范围分别为[ωmin，ωmax]、[Umin，Umax]，ωmax=50.2Hz，ωmin=49.0 Hz，Umax-Un=Un-Umin=10%×Un。

5 算例分析

在PSCAD／EMTDC环境下搭建了图1所示结构的微电网平台，具体参数如下。

为了验证所设计控制策略的可行性和鲁棒性，微电网的运行过程涉及多种工作模式：1.0 s前并网运行；1.0 s时与主电网断开独立运行；2.0 s时独立运行状态下发生负荷突变，Load3突降为16kW／5kVar；3.0 s时重新联到电网。

5.1 基于小生境遗传算法的微电网运行优化

根据第4节所述优化过程，基于小生境遗传算法优化微电网的运行性能。小生境遗传算法的种群数量为20，最大进化代数为100。优化后的微电网控制参数[mp，md，nq，nd]=[2.44×10-5，0.72×10-5，5.13×10-4，1.29×10-5]。 由图9优化过程中目标函数f的收敛曲线可以看出，小生境遗传算法能够较快地收敛到全局最优。图10为第30代至第35代进化时，微电网中DG1和DG2输出的有功功率变化曲线。随着种群的不断进化，微电网稳态运行的误差和振荡越来越小，而且动态切换过程的响应时间越来越短，超调也越来越小，验证了所采用的优化方法可以不断改进微电网控制的稳态性能和动态特性。

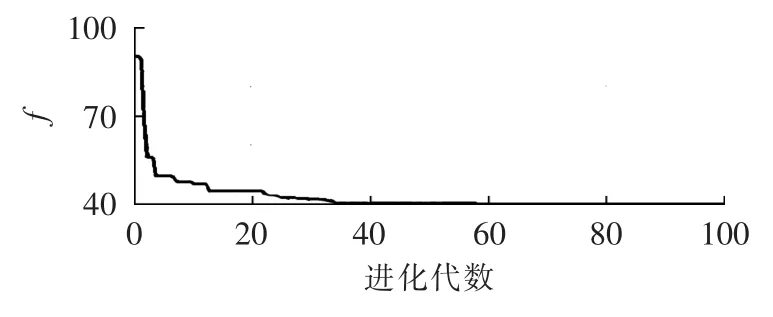
图9 目标函数的收敛曲线Fig.9 Convergence curve of objective function

图10 微电网的有功功率优化过程Fig.10 Process of active power optimization for microgrid

5.2 优化后的微电网运行特性

基于小生境遗传算法优化后的微电网，DG1和DG2输出的有功功率和无功功率分别如图11（a）和（b）所示，交流母线频率和电压分别如图 11（c）和（d）所示。由于断开前微电网从主电网吸收部分功率，所以独立运行后微电网中DG输出的有功功率和无功功率均增加。在独立运行时，微电网能够快速准确地实现DG间负荷功率分配，且电压幅值和频率都稳定在允许范围内。 图 11（e）、（f）为 DG 输出电流及局部放大图，表明系统均流特性良好，且重新并网过程中无明显的冲击电流。

从优化后的微电网运行特性可以看出，本文所设计的控制策略及优化方法有效实现了微电网在不同工作模式间的平滑切换，且在不同工作模式下都能快速无振荡地进入稳态运行，保证了系统稳定性的同时提高了动态性能。

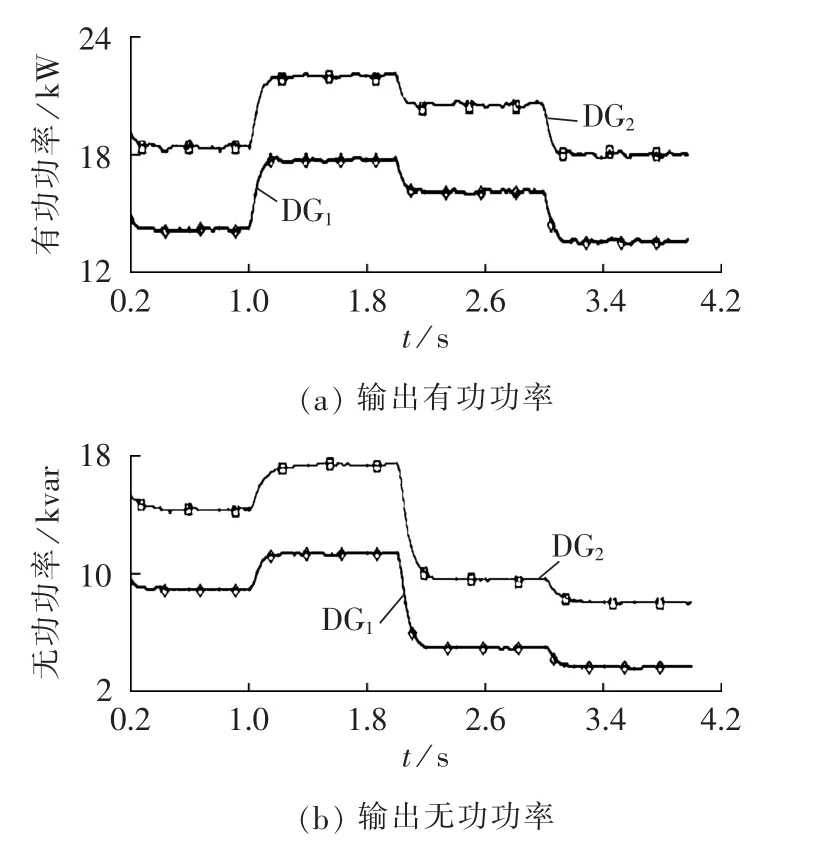
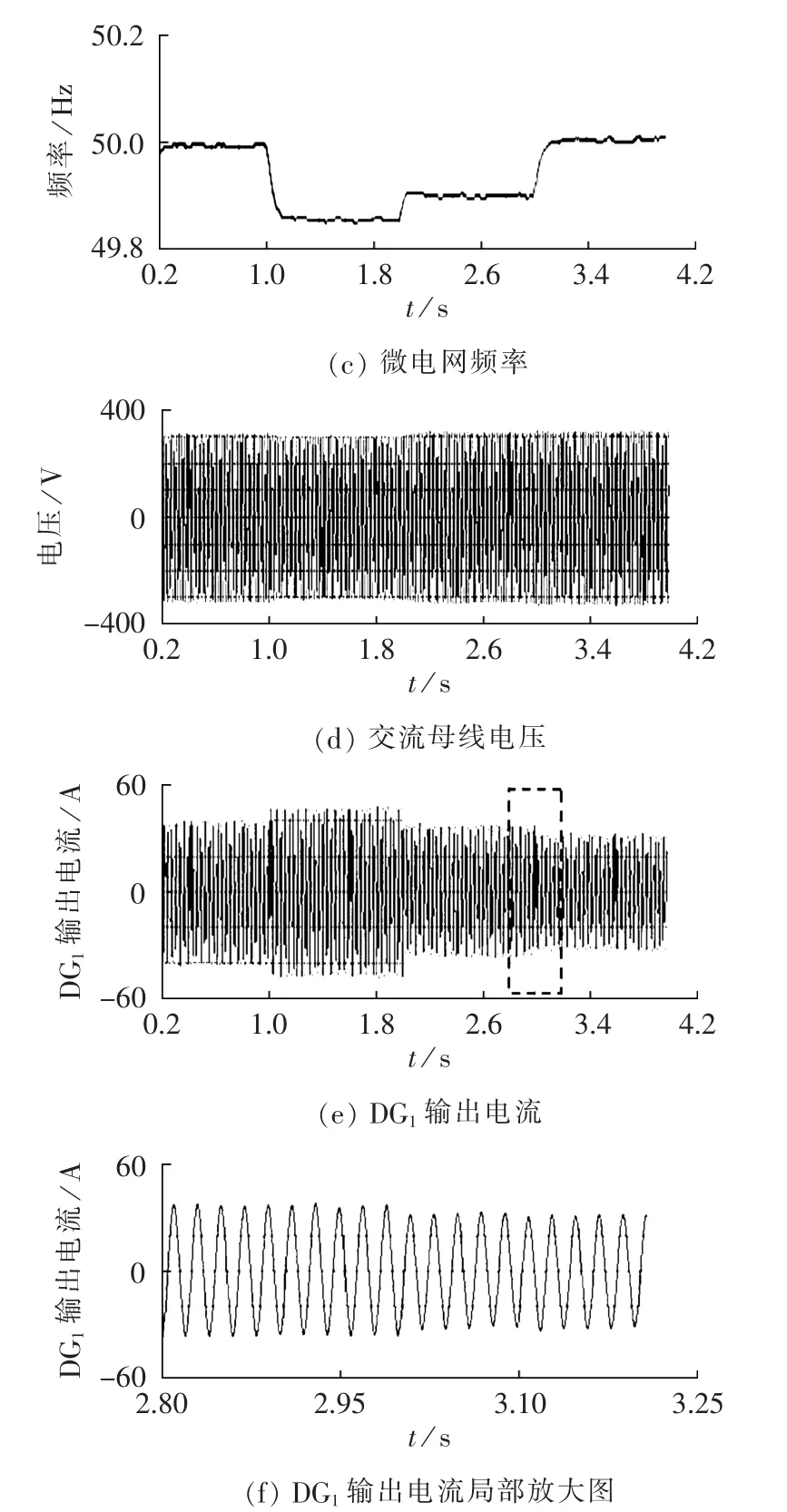
图11 微电网运行特性Fig.11 Operating performance of microgrid

5.3 优化方法的鲁棒性测试

基于小生境遗传算法的微电网运行优化考虑了微电网的多种运行状态，从而保证了本文优化设计的控制策略在多种工作模式下都具有较强的鲁棒性。

图12为在初始种群不同的情况下，多次优化过程的目标函数收敛曲线。可以看出，目标函数在多次优化过程中都收敛于相同值，表明了基于小生境遗传算法的优化方法对于初始种群具有较强鲁棒性，能够有效避免非全局性收敛。

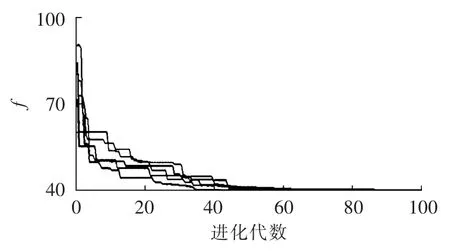
图12 多次运行的目标函数收敛曲线Fig.12 Convergence curve of objective function for multiple runs

6 结论

为了提高微电网在不同工作模式下以及模式切换过程中的稳态特性和动态性能，本文提出了一种包含改进动态特性的功率分配控制器、带前馈补偿的电压电流双闭环控制器的微电网控制策略，并基于小生境遗传算法优化微电网运行特性。基于小信号动态模型分析了影响微电网运行特性的主要控制参数及其优化取值域，有效提高了优化过程的计算效率。构建了基于PSCAD／EMTDC时域仿真模型的优化目标函数，采用小生境技术和自适应技术改进的遗传算法对所提出微电网控制策略的主要参数进行了优化设计。微电网多种工作模式和模式切换的时域仿真以及自适应小生境遗传算法保证了微电网控制策略及优化方法的鲁棒性。对于具有不同原动机部分的DG及不同拓扑结构的微电网的控制与优化值得进一步研究。同时，微电网运行涉及的因素较多，其运行优化的目标函数建模有待后续研究。