电动汽车充电对配电网负荷的影响及有序控制研究

王 建，吴奎华，刘志珍，吴奎忠，孙 伟

（1.山东大学 电气工程学院，山东 济南 250061；2.山东电力经济技术研究院，山东 济南 250001；3.吉林电力有限公司，吉林 长春 130021；4.山东电力集团公司，山东 济南 250001）

0 引言

利用电能替代传统石油燃料，可减少温室气体排放和对石油进口的依赖[1]。目前，国际上各大汽车公司已开始电动汽车EV（Electric Vehicle）产业化的进程，而大规模电动汽车接入电网势必会对电网规划运行产生影响[2-3]。

无序充电将会对电力系统安全、经济运行带来严重的负面影响。利用峰谷分时电价，引导用户采用低谷时间充电，对削峰填谷有一定效果。而协调充电或智能充电，被认为是解决协调这一系列问题的有效措施之一[4-5]。

调度机构直接对每台接入的电动汽车进行统一调度，实现有序控制，但规模庞大，变量维数激增，收敛困难[6]。 本文通过中间管理者运行架构[7]，提出集中、分布相结合的优化控制策略以解决该问题。文献[8]采用粒子群算法，以用户获利最大为目标函数，但未考虑充电电流约束。文献[9]建立的模型中则未考虑电池寿命等实际制约因素和终端接入网的随机性。本文优化控制模型考虑了充电电流、电池寿命等约束条件，更接近实际。

电动汽车充电负荷影响因素较多，模型建立困难。本文根据电动公交车充电实测数据和美国交通部对全美居民出行调查（NHTS）最新数据，建立充电负荷模型，研究电动汽车不同渗透率下对电网的影响。针对电动汽车规模化应用及无序充电对电网规划运行带来的负面影响，提出时段控制策略和智能优化控制策略，采用集中式与分布式结合的优化控制理念，建立了协调控制模型，通过对山东电网不同充电情景下的仿真，验证了充电负荷模型和智能优化控制策略的有效性和可行性，对未来电网的规划运行有一定参考价值。

1 电动汽车充电负荷特性建模

为了研究电动汽车充电对电网的影响，首先需要根据负荷特性建模。影响电动汽车电力需求的因素主要包括电池特性、充电模式、用户行为习惯等，难点在于充电行为时空不确定性。

本文从分析电动汽车充电行为入手，分为以公交车为代表的商用车和以私家车为主的乘用车两大类。前者充电行为及行驶里程规律相近，都较为有序，易实现时间调控；后者使用和充电随机性、灵活性较大。结合山东实际情况，本文将以公交车和私家车作为典型研究对象。

1.1 电池特性

本文电动公交车参数依据山东焦庄充电站电池实际参数选取如下：电池容量为163.8kW·h，每100 km耗电为113 kW·h，初始容量为10%，充电效率为90%，快速充电功率为80 kW。电池容量在一定程度上影响制造成本和充电性能，因此小容量电池更易普及。电动私家车电池参数根据市面有代表性的丰田RAVA4、比亚迪F3DM等车型综合选取，目前国内居民用电通常采用220 V／16 A、220 V／25 A这2种规格，受家庭充电设施所限，取充电功率3 kW。电动私家车具体参数如下：电池容量为30 kW·h，每100 km耗电为15kW·h，初始容量为10%，充电效率为90%，充电功率因数为0.95，正常充电功率为3.0 kW。

1.2 充电模式

按照充电电流大小，其充电模式可分为快充和慢充。前者电池充电电流通常在1C～3C（如2C表示电池在理想状态下0.5 h充满，其他同理）范围内，主要通过充换电站进行充电，充电时间短；后者主要针对大量低电压充电桩（主要集中于居民楼、办公区停车场）和家庭慢充方式，充电电流一般在0.1 C～0.5 C，通常需要5～8 h充满。依据薛家岛一体化示范充电站运行经验，取充电桩充电效率93%，功率因数0.95，充电功率9.5 kW。

1.3 用户行为

用户行为是影响电动汽车功率需求的关键因素，主要包括开始充电时刻和日行驶里程两方面。根据2009年NHTS数据[10]，结合山东私家车行驶特点，得到日行驶里程电动私家车分布见图1。

图1 日行驶里程Fig.1 Daily trip length

拟合[11]得出日行驶里程概率密度函数：

其中，a1、a2和 σD1、σD2分别为电动汽车日行驶里程正态分布函数的系数和标准差，μD1=17.79，μD2=38.35。该函数满足正态分布。

汽车最后一次行程结束时刻满足以下概率密度分布函数[11]：

式（2）符合分段正态分布，其标准差均为σs，而数学期望则分别为μs和μs-24。假设最后一次行程结束时刻即为开始充电时间，根据式（1）、（2）和电动私家车参数可得到电动私家车充电负荷特性。

本文通过对山东焦庄电动公交车充电站24 h负荷，以10 min为间隔进行充电功率实测，得到充电站日常运行负荷数据，并利用最小二乘法[12]进行曲线拟合得到公交车充电负荷曲线如图2所示。

由图2可以看出，曲线基本符合正态分布，考虑到安全、运营等因素，公交车每天需充电2次，晚间充电时间为非运营时间（20∶00 至次日 05∶00），统一集中充电，采用慢充模式，白天运营时间内的充电是在运营中为公交车补充充电，公交车难以长时间停留，一般采取快充模式。

图2 电动公交车充电负荷曲线Fig.2 Charging load profile of electric bus

2 电动汽车充电对配电网负荷特性的影响

《中国汽车产业发展报告（2012 年）》[13]中提出，未来20年是我国电动汽车产业发展的关键时期，将重点推进纯电动汽车和插电式混合动力汽车产业化，提升我国电动汽车产业整体技术水平。预测2030年山东私家车总量为2284万辆，按目前山东私家车与公交车比例，2030年山东公交车为12.6万辆。

根据山东电网“十二五”及中长期规划成果，以山东电网2030年夏季某日负荷曲线为例，假设2030年电动私家车占私家车总量的比例分别为10%、20%和50%，电动公交车占公交车总量的比例分别为25%、35%和50%，分析比较在不同渗透率情况下，电动汽车无序充电对电网日负荷曲线的影响见图3。

由图3可见，随着电动汽车规模化发展，大量无序充电负荷与原有峰值时间重叠且持续时间增长，在高渗透率情景下会使电网峰值负荷显著增加。不仅增加调峰容量需求，还可能导致电能质量下降、损耗增加等系列问题。图3中，10%＋25%表示电动私家车占10%、电动公交车占25%，后类似。

图3 无序充电对山东电网2030年日负荷曲线的影响Fig.3 Impact of uncoordinated charging on daily load curve of Shandong Grid in 2030

3 优化控制策略

3.1 时段控制策略

电动汽车有序充电的实现依赖高级计量体系AMI（Advanced Metering Infrastructure）和智能电网通信技术的软硬件支持，因此，利用激励政策引导用户避峰充电在短期内将会是一种易行、有效的调控措施。本文结合延迟充电和低谷充电[14]2种模式的特点，依据目前国内对时段分时电价的划分原则和山东地区峰、谷、平多个时段的具体划分，并考虑电动汽车的行驶规律，提出了针对山东电网充电行为的时段控制策略。

对电动汽车充电的控制或调度前提是电动汽车处于驻留状态，并接入电网。因此电动私家车驻留时间长短、所处时间段是调控策略的依据之一。式（2）中 μs=17.6，σs=3.4，即用户下班到家高峰时间集中在18∶00左右，驻留时间直到次日06∶00左右，本文在MATLAB7.0中采用蒙特卡洛模拟方法，结合NHTS统计数据，得到电动私家车最后一次行程结束时刻的累积分布如图4所示。

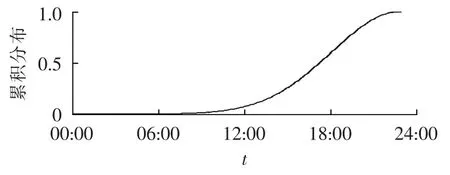
图4 电动私家车最后一次出行结束时间Fig.4 Ending time of last trip of private electric car

如图 5[15]所示，在 06∶00—09∶00 时间段内，驻留时间超过6 h的汽车可达总数的10%以上，使得电动汽车在下午负荷高峰前进行长时间充电成为可能。因此，除夜间低谷充电外，避开尖峰时段，在白天分别增设 08∶00—10∶00 和 12∶00—14∶00，作为电动私家车快速补充电量的调控时段，引导用户利用办公区停车场充电设施进行充电。06∶00—09∶00开始的慢充则在15∶00负荷高峰之前完成。图中时段编号1～12 分别对应 06∶00 — 07∶00、07∶01 — 08∶00、08∶01—09∶00、09∶01—10∶00、10∶01 — 11∶00、11∶01 — 12∶00、12∶01—13∶00、13∶01—14∶00、14∶01—15∶00、15∶01 —16∶00、16∶01—17∶00、17∶01—18∶00。

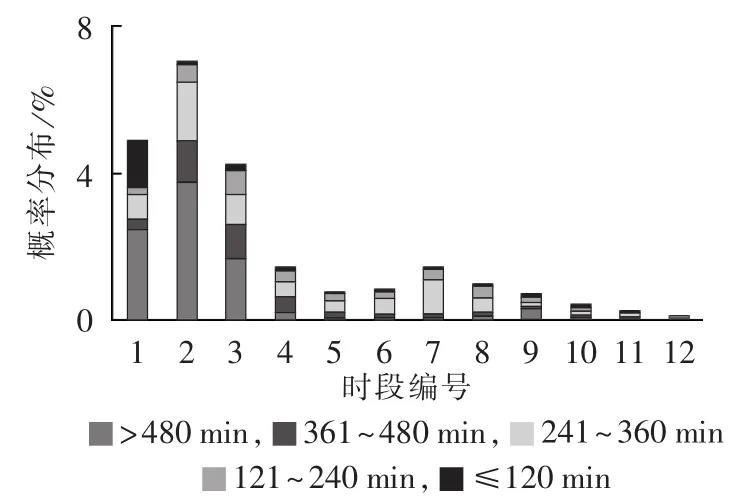
图5 电动私家车06∶00—18∶00驻留时间分布Fig.5 Dwell time distribution of private electric car during 06∶00-18∶00

根据电动公交车和电动私家车不同行驶规律，将每天分为不同时段按不同充电模式加以引导、调控，各充电模式占充电总数比例分布见图6。

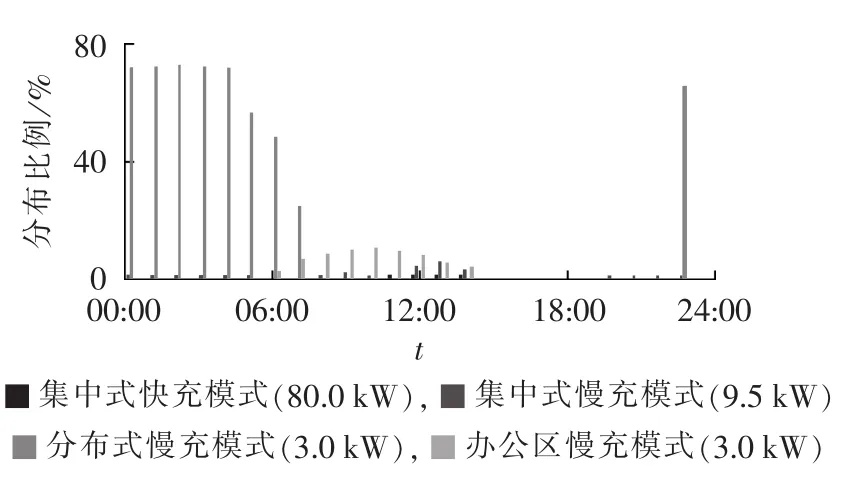
图6 不同充电模式各时段充电分布比例Fig.6 Distribution of EV charging period for different charging modes

根据各时段电动汽车数量分布和充电模式，即可得出总充电需求，进而分析本文所提出的时段控制策略对山东电网负荷的影响。由第4节可以看出，时段控制策略可有效地实现电动汽车充电负荷的转移，避免无序充电峰值与自然峰值的重叠，在一定程度上能够改善负荷曲线，但该方法缺点在于机械化，缺乏灵活性。针对该缺点，在满足用户利益的前提下，本文进一步提出有序充电的智能控制策略，并和时段控制策略加以比较。

3.2 智能充电优化控制模型

电动汽车充电优化控制考虑的2个重要因素是：规模庞大；随机变量较多，如电池充电状态SOC（State Of Charge）、充放电时间、充电地点等。 文献[7]中提出通过中间管理者来解决充电用户大范围分散决策与电网调度集中决策之间的矛盾，回避时空不确定性对电网调度带来的问题，充分发挥目前电网集中调度、运行优点。本文提出借助中间管理者将集中优化控制与分布式优化控制相结合的优化控制策略实现有序充电的智能控制。

3.2.1 集中式优化控制

集中式优化控制的目标为减小负荷峰谷差，使负荷波动最小化，实现平抑负荷。假设有L个中间管理者，第l个中间管理者管理Ml辆电动汽车，将全天24 h平均分为N个时段，间隔为15 min，负荷最小化目标函数如下：

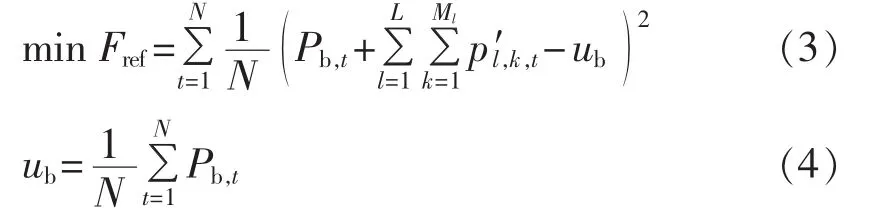
其中，Pb，t和ub分别为电动汽车未接入时电网t时段的负荷和各时段的平均负荷水平；p′l，k，t为第 l个中间管理者第k辆电动汽车在t时段内的充电功率需求预测，p′l，k，t＞ 0 表示充电，反之表示放电，本文暂不对后者进行讨论。

3.2.2 分布式优化控制

中间管理者通过电网通信技术，将每个时间段接入电网的电动汽车的开始充电时间、电池初始状态和充电功率等信息实现动态检测。在每个时段开始时，通过动态时间窗将更新信息与优化过程有机结合，并根据电网与中间管理者在前一阶段优化过程所得的参考优化功率和24 h动态电价，按照式（5）对个体充电方案进行优化。

优化目标是各时段充电需求与集中优化控制结果之间的偏差、用户充电成本最小化，同时考虑延长电池寿命。目标函数如下：

其中，ct为实时浮动电价；dl，k，t为电池寿命表示项；β为影响系数，此处取1；pl为t时段内各电动汽车实际充电功率与电网分配给中间管理者的参考优化功率（集中优化控制结果）之间的偏差；αl，k，t和 pl，k，t分别为第l个中间管理者所管辖的第k辆电动车在t时段内的动态参数和实际充电功率；P′l，t为电网在 t时段内分配给第l个中间管理者的参考优化功率。

为了定义第k辆电动汽车充放电状态和时间段t的关系，通过动态时间窗 ω（t）定义矩阵 AMmax×Nl，其中，Mmax=max｛M1，M2，…，Ml｝，Ml为第 l个中间管理者的电动汽车总数，αl，k，t（k=1，2，…，Mmax；t=1，2，…，N）为矩阵 AMmax×Nl的元素，αl，k，tє｛0，1｝，当 ω（t）落在第 k 辆电动汽车充放电时段中时，αl，k，t=1，否则表示非调控状态，等于0。

电池寿命通常通过充放电频繁程度来衡量[16]。本文利用相邻时间段的充电负荷变化率来间接表示充放电对电池寿命的影响，如式（7）所示。

3.2.3 优化控制约束条件

第l个中间管理者所有充电设施所能提供充电功率上限，以及每辆电动汽车受充电设施制约的最大充电功率，分别如式（8）、（9）所示。

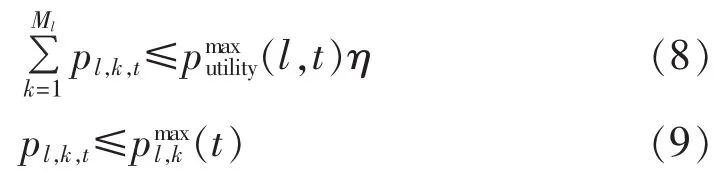
电池充电约束：

电池放电约束：

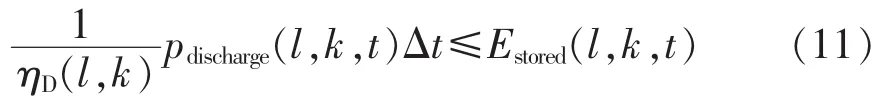
其中，pmutailxity（l，t）为第 l个中间管理者在 t时段内所有充电设施所能提供充电功率上限；η 为充电效率；pml，akx（t）为每辆电动汽车受充电设施制约的最大充电功率；ηc（l，k）、ηD（l，k）和 pcharge（l，k，t）、pdischarge（l，k，t）分别为第l个中间管理者的第k辆电动车电池充、放电效率以及电池充、放电功率；Ebattery-limit（l，k）为由 SOC 和电池温度决定的变量，本文假设该变量为常数，即电池容量 Ebattery-capacity（l，k）；Estored（l，k，t）为电池存储电量。

充放电电流约束：

其中，I0为起始充电时最大电流，由电池初始SOC和物理特性决定；α为放电电流指数，由充电电路和电池特性决定。

电池SOC约束：

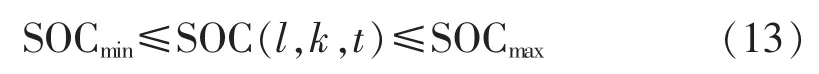
其中，SOC（l，k，t）为 Estored（l，k，t）与 Ebattery-capacity（l，k）的比值，为保护电池，防止电池过充、过放，延长电池使用寿命，规定 SOCmin=0.1，SOCmax=max｛0.9，SOCuser｝，SOCuser为用户充电时设置的充电上限。

3.3 智能充电优化控制实现步骤

上述模型是一个动态规划问题，本文采用AMPL建立了模型，调用外部求解器CPLEX 12.2求解。步骤如下：中间管理者提出充电需求计划，电网调度机构采用相似日法[17]进行负荷预测，利用集中式优化控制方法计算得出集中式优化控制结果，分发给中间管理者，作为中间管理者进行优化控制的参考。中间管理者利用动态时间窗检测充电相关信息（充电起始时间、电池状态和充电功率等），采用分布式优化控制策略，优化控制各充电用户的充电时间，并及时更新终端变量，反馈给电网调度机构用于调整集中式优化控制结果。算法流程图如图7所示。

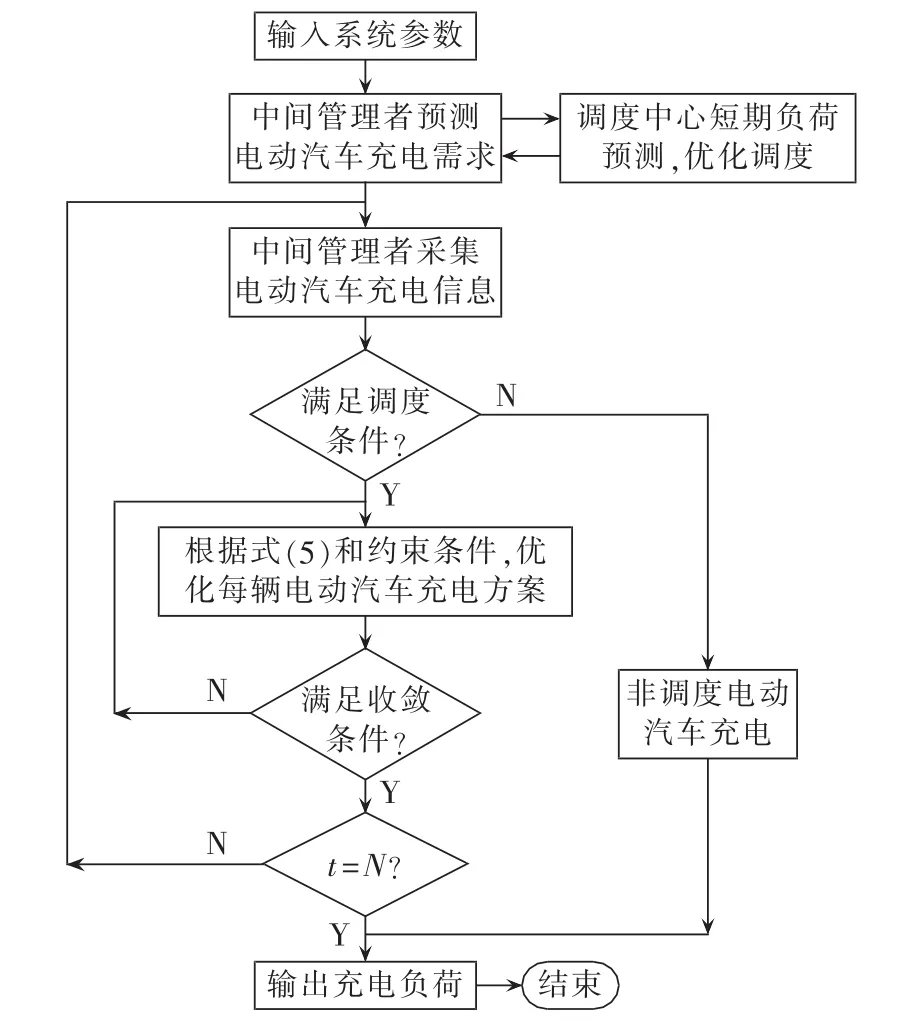
图7 算法流程图Fig.7 Flowchart of algorithm

4 优化控制策略对配电网影响

根据山东电网“十二五”及中长期规划成果，结合山东电网未来用电结构调整、需求侧管理、产业结构变化及智能电网建设等相关因素，得到山东电网2030年夏季某日负荷曲线，并以此为基础研究时段控制和智能充电优化控制策略对配电网的影响。

本文结合车辆驻留时间、行驶规律所划分的时段，可以在一定程度上实现削峰填谷，然而由图8可以看出，在渗透率为50%时，12∶00左右出现了新的负荷峰值；此外，随着电动汽车逐渐充满电池，夜间充电负荷在原有低谷时间05∶00左右反而开始下降。因此，时段划分具有机械性，无法根据日负荷情况自动进行动态调整。

由图9可知，通过实时电价和负荷波动最小化的优化控制策略，在05∶00左右，充电负荷并未出现下降。另外，浮动电价使得充电负荷避开通常10∶30和19∶00左右的2个尖峰，对于将负荷从峰值段转移到其他区段具有较为明显的效果，尤其是当电动私家车和公交车市场占有率分别为50%时，日峰谷差缩减到25 GW，最小日负荷率为84%，智能充电优化效果显著。

图8 时段控制对山东电网2030年日负荷曲线的影响Fig.8 Impact of period control on load curve of Shandong Grid in 2030

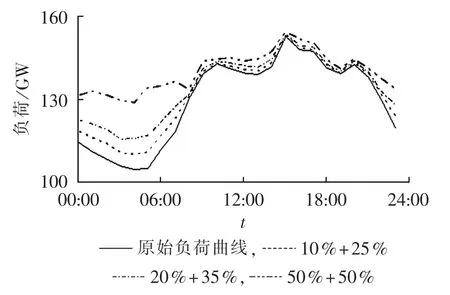
图9 有序充电对山东电网2030年日负荷曲线的影响Fig.9 Impact of coordinated charging on load curve of Shandong Grid in 2030

5 结语

本文从分析电动汽车的充电行为入手，分别以电动公交车的充电功率实地调研数据和2009年NHTS报告为基础，利用最小二乘法和概率统计方法建立充电负荷模型，研究电动汽车无序充电对电网的影响。针对电动汽车规模化应用及无序充电对电网规划运行带来的负面影响，提出时段控制策略和智能优化控制策略，但时段控制策略灵活性较差。提出采用集中式与分布式结合的优化控制理念，建立了协调控制模型，引入动态时间窗实时更新电动汽车充电的动态信息，在满足充电需求前提下，实现平抑负荷、用户充电成本最小化的目标，同时对模型进一步改进，增加电池实际约束条件，更符合实际情况。以山东电网2030年某日负荷曲线为例，分析无序充电、时段控制充电、有序充电对配电网负荷的影响，验证了充电负荷模型和智能优化控制策略的有效性和可行性，对未来电网的规划运行有一定的参考价值。