HHT法的基本原理及其应用探讨

张丽娜， 李凤臣， 彭必全， 袁青竹， 郑喜亮

(1.东华理工大学建筑工程学院，江西南昌 330013;2.中冶赛迪工程技术股份有限公司，重庆 400013)

对于给定的非平稳信号，传统的信号处理方法是基于Fourier变换的频谱分析法，Fourier变换在任一频点上的值是信号在整个时域上的统计平均值(应怀樵，1985)，因此不能准确反映非平稳信号的时变特征，且要求分析信号是稳态的、线性的。近年来，基于小波变换的时频分析法受到了广泛关注(Kareem et al.，1996，Hou et al.，2000，李洪泉等，2003)。小波分析能同时提供振动信号的时域和频域的局部化信息，但小波分析法仍然以Fourier变换为基础，是对Fourier变换的改进，在识别振动信号包含的非线性和非稳态特性时，需假定先验的小波基函数形式，同一信号采用不同的小波基函数可能导致分析结果差别较大，难以对信号做精确的时频域分析。然而，在土木工程领域，环境激励下的结构振动响应信号多为非线性、非平稳信号，传统的Fourier变换和小波分析所提供的时频分析方法在实际应用中存在一定的局限性(钱七虎，2004，孙占学等，2004)。目前发展的 Hilbert-Huang Transform(HHT)方法是由Huang等(1998)提出的一种全新的信号处理方法，能够在时频域内对信号进行分析处理，其依据信号本身的局部特征信息进行自适应分解，不需要预先设定参数。因此，克服了依赖预测人员主观经验的问题，且具有较强的抵抗噪声能力，能更好地反映信号的本质特征。这一方法在此后短短几年内，便在地质、海洋、医学等工程领域得到了成功应用。实践表明，该方法是一种较为理想的非线性和非稳态信号的分析工具(喻晓今，2004，杨恒山，2008)。

本文应用HHT对冲击荷载作用下结构瞬态响应的信号进行分析，观察结构的内部物理特征，更加深入的了解结构在荷载作用下的响应。

1 Hilbert-Huang变换的基本原理

HHT包含两大部分:经验模态分解(Empirical Mode Decomposition，EMD)和 Hilbert谱分析(Hilbert Spectrum Analysis，HSA)，其核心是EMD分解(李凤臣等，2012)。经验模态分解是建立在任何信号都包含不同的单一固有振动模态的假设上的。无论是线性还是非线性信号，每个固有模态都代表一个简单的振动，即具有相同数目的极值和零点的振动。在任何给定时间内，信号可能有很多共同存在的振动模态，一个个叠加在一起，结果就组成了复杂的信号数据。这些单一的振动模态就叫做固有模态函数(Intrinsic Mode Function，IMF)。

HHT处理非平稳信号的基本过程是:首先利用EMD方法将给定的信号分解为若干固有模态函数(IMF)，然后对每一个IMF进行Hilbert变换，得到相应的Hilbert谱，最后将所有IMF的Hilbert谱叠加就会得到原始信号的Hilbert谱。EMD分解过程是通过一种称为筛选的计算步骤来实现。设x(t)代表需要分解的信号。首先找出x(t)上所有的极值点，用三次样条曲线连接各极大值点形成x(t)的上包络线，同样连接各极小值点形成下包络线，确保x(t)上的所有点在上下包络线之间。定义上下包络线之间的均值为m1，x(t)与m1的差定义为

随后，将x(t)与C1的差:r1(t)=x(t)－C1作为新的数据重复上述筛选过程，可得第二阶IMF分量C2。当IMF分量Cn或余量rn小于预先设定的值，或者余量已经成为单调函数时，则整个筛选过程结束。经过上述步骤后，x(t)可分解为n阶IMF分量及余量rn的和，即

对任意一个时间函数 x(t)，其Hilbert变换y(t)定义为

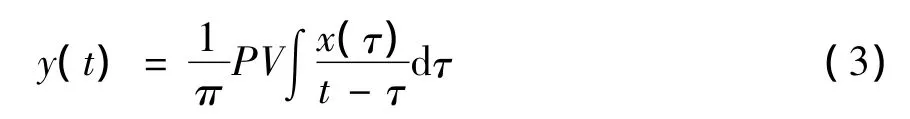
其中PV为柯西主值。则对应于x(t)的解析信号z(t)为

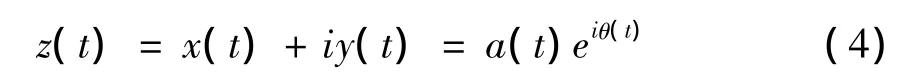
其中a(t)称为信号x(t)的瞬时振幅，θ(t)称为信号的瞬时相位，两者按下式计算

由瞬时相位可以得到信号的瞬时频率

对原始信号的每一阶IMF进行Hilbert变换后，原始信号可以表达成一下形式

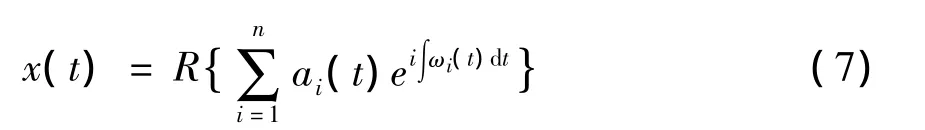
其中R代表函数的实部。此处，原始信号x(t)的表达式中，已经去除了rn，因为rn是一个单调函数或者常数。

式(7)中既有瞬时振幅ai(t)，又有瞬时频率ωi(t)，且都是随时间变化的。而信号x(t)的傅立叶变换为

其中振幅ai和频率ωi都是常数。所以，同傅立叶变换相比，HHT中的IMF是一种广义的模态，具有随时间变化的振幅和频率。

根据式(7)，可将信号x(t)表示在一个三维图中，在联合的时间-频率平面上，将瞬时振幅ai(t)的轮廓画出来。信号x(t)的这种时频表示即为其Hilbert谱，H(t，ω)，其定义为

2 Hilbert-Huang变换有效性验证

下面举个简单的例子，来说明HHT的有效性。两个频率不同的正弦信号叠加在时域的图形如图1所示。

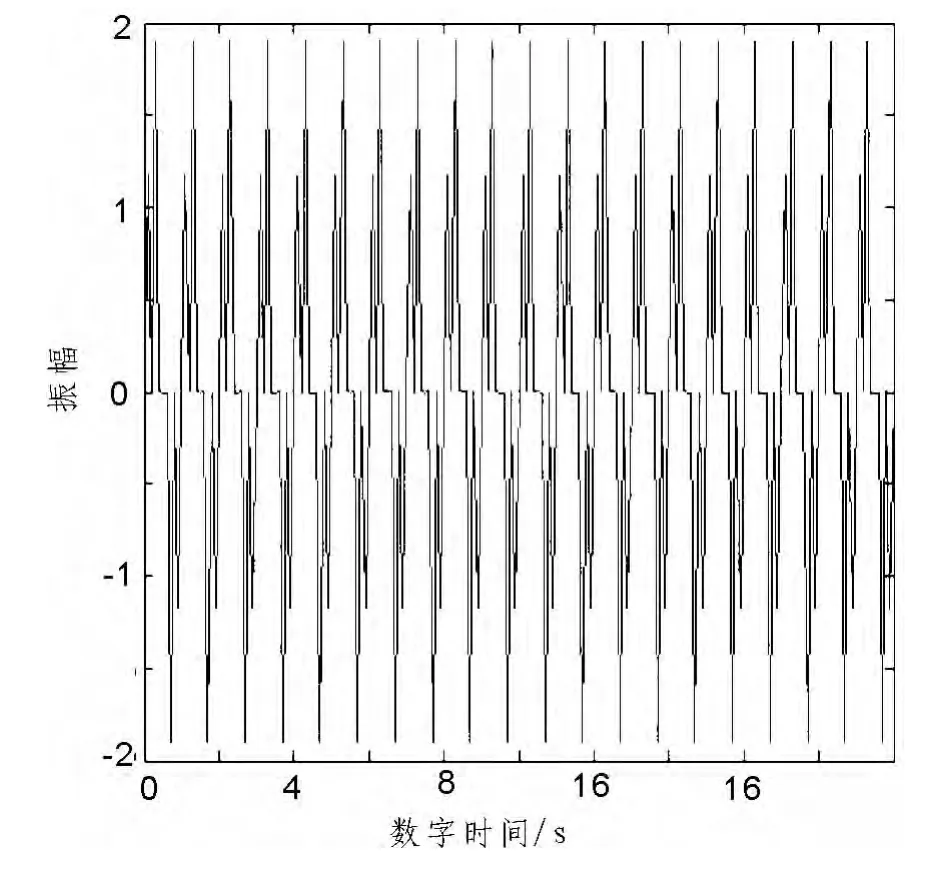
图1 正弦混和信号Fig.1 mixed sine signal

其表达式为

取信号从0～20 s的数据进行HHT变换，得到EMD和Hilbert谱分别如图2和图3所示。

图2 信号的EMD分解Fig.2 EMD decomposition of signal

图3 信号的Hilbert谱Fig.3 Hilbert spectrum of signal

由图2可以看出，EMD分解将原始信号中所含的两个不同频率的正弦信号完整的分离了出来，达到了很好的滤波效果。图3则反映了原始信号中能量随时间和频率的分布，其中可以清楚的看到两个IMF分量c1(t)和c2(t)，所占能量比重很高。其他几个是经验模态分解时的误差，所占能量很少。所以，可以看出HHT是一种十分有效的信号分析方法。

3 应用HHT处理MRRM计算梁瞬态响应的数据

梁在冲击荷载作用下的瞬态响应为非平稳信号，具有频率随时间变化的特性，可以用HHT方法对其进行分析，看其在时间和频率域内能量的分布情况，研究结构自身频率与响应频率之间的关系。

现在就对一两端固定的Timoshenko单跨梁瞬态响应信号进行分析。如图4所示，两端固定的单跨低碳钢梁几何物理参数为:梁高h=0.5 m，梁宽b=0.04 m，梁长度 L=2 m，密度 ρ=7 850kg/m3，截面积 A=0.002m2，弹性模量 E=206 GPa，剪切模量G=79 GPa，剪切因子κ=0.833 3。其冲击荷载为

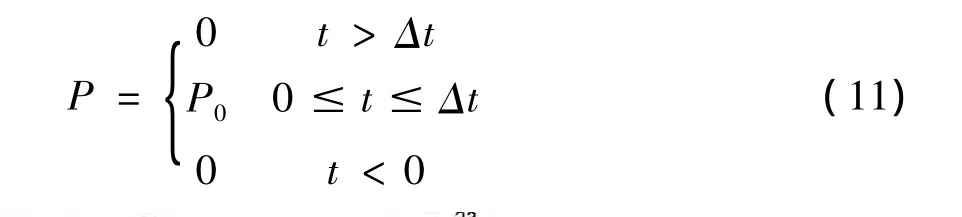
图4 两端固定的Timoshenko单跨梁Fig.4 Single-span Timoshenko beam with two end fixed

通过Matlab软件编程，利用MRRM法进行单跨Timoshenko梁的动力响应计算，对其动力响应分别进行快速傅立叶变换(FFT)和HHT变换。现取其跨中加速度信号进行分析，原始数据a21的数据结果如图5所示。

原始信号中有几个明显的波动，主要是波经过两端支座反射，经过一定时间后，回传至该观察点发生叠加的结果。

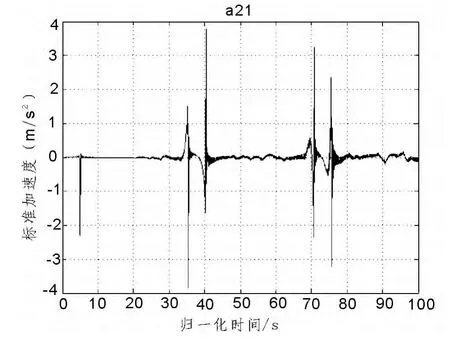
图5 跨中加速度a12响应信号Fig.5 Acceleration response signal of a12 at mid-span

加速度响应信号a21的Fourier谱如图6所示。从图6中可以看出，波峰所对应的频率值是结构的各阶自振频率，主要是结构在外荷载激励下，其自振频率与外荷载发生共振，导致该点处幅值增大，从图6中可以粗略的得到结构的自振频率。

图6 a21信号的Fourier谱Fig.6 Fourier spectrum of a21

原始信号a12经过EMD分解后的结果如图7所示。从图7可以看出，前三阶IMF分量有比较明显的波动现象，后面几阶IMF分量趋于平缓，这表明前几阶IMF分量反映了结构瞬态响应的高频部分的特性，而后几阶IMF则反映了低频部分的特性。EMD分解能够将信号中高频和低频的部分分离出来，并能够简洁明了的将低、高频信号反映在IMF图中。

接下来对原始信号进行Hilbert变换，得到响应的Hilbert谱，更能够看到信号能量在低频和高频段的分布情况(图8)。从图8中可以看出，频率较低且较为平直的几条线为结构的自振频率，其数值与图6中的自振频率相等。当结构不受外界荷载冲击时，表现的是结构自身的自振频率;当受外界脉冲作用时，表现出来的频率比较丰富，即图中三处起伏明显的地方。这表明结构受外界荷载作用后，产生波动，其高频的部分被激起，且随时间变化，所以在Hilbert谱中会出现高频的特性，这个特点是Fourier谱无法展示的。

同时，对于图5中跨中加速度a12的响应，在无量纲时间5处，信号出现大幅度波动，表明卸除荷载过程，出现一个脉冲。波经过两端支座反射后，回传到跨中经叠加后产生了两个明显的波动。在EMD分解中，也可以看到三处明显的波动现象，在Hilbert谱中则表现在三处有高频出现的地方。同样可以看出，高频波动所占比例不大，主要还是以低频波动为主，体现了结构本身自振频率的特性。

图7 a21信号的EMD分解Fig.7 EMD decomposition of a21

图8 a21信号的Hilbert谱Fig.8 Hilbert spectrum of a21

4 结论

本文重点利用HHT对回传射线矩阵法计算的梁的瞬态响应信号进行了分析处理，并得出以下结论:

(1)HHT方法的基函数具有自适应性，比以往的各种方法更适合非平稳信号的分析和处理。

(2)HHT方法不仅可以将瞬态信号中低频和高频的部分通过EMD分解分离出来，还可以通过Hilbert谱展示信号能量在时频域内的分布，可以更为清楚地了解信号中低高频部分的分布情况，更为深入的了解信号的本质。

(3)通过分析梁瞬态响应信号，发现梁在受到外界突加荷载时，在短时间内产生高频震动，即所谓的波动现象;当荷载作用一段时间后，结构才产生频率相对较低的振动现象。

李凤臣，郑喜亮，张丽娜.2012.Timoshenko梁的动力问题探讨——基于回转射线矩阵法的动力响应分析［J］.东华理工大学学报:自然科学版，35(4):438-442.

李洪泉，董亮，吕西林.2003.基于小波变换的结构损伤识别与试验分析［J］.土木工程学报，36(5):52-57.

钱七虎.2004.深部岩体工程响应的特征科学现象及“深部”的界定［J］.东华理工学院学报.27(1):1-5.

孙占学，朱永刚，张文.2004.矿物-水反应的地球化学动力学研究进展［J］.东华理工学院学报，27(1):14-18.

杨恒山.2008.向量加权平均值在桥梁控制网平差中的应用［J］.东华理工大学学报:自然科学版，31(3):256-258.

应怀樵.1983.波形和频谱分析与随机数据处［M］.北京:中国铁道出版社.

喻晓今.2004.求梁位移的比拟梁法［J］.东华理工学院学报，27(4):398-400.

Hou Z，Nonri M，Amand R S.2000.Wave based approach for structural damage detection［J］.Journal of Engineering Mechanics，ASCE，126(7):677-683.

Huang N E，Shen Z，Long S.R et al.1998.The empirical mode decomposition and the Hilbert spectrum for non-linear and non-stationary time series analysis［A］.Proceedings of the Royal Society of ondon［C］.A454:903-995.

Kareem A，Gueley K.1996.Damping in structures Itsevaluation and treatment of uncertainty［J］.Journal of Wind Engineering and Industrial Aerodynamics，59(2):131-157.