非负矩阵分解和Curvelet在遥感图像融合中的应用

曾立庆， 童怀水

(1.东华理工大学江西省数字国土重点实验室，江西抚州 344000;2.东华理工大学理学院，江西抚州 344000)

在图像处理的诸多研究领域中，图像融合技术一直是近些年的研究热点，数据融合技术是将多个已配准的多传感器图像采用适当的方法融合成一幅具有更好的空间分辨率或光谱特性的融合图像。融合的方法有早期的IHS变换、PCA方法、金字塔变换、小波变换等，以及近些年较新的多尺度分析方法，如 Ridgelet变换、Curvelet变换、Contourlet变换等。一些学者在采用上述方法的同时，还结合其他领域的方法进行研究，比如结合支持向量机SVM(Support Vector Machine)、模糊理论、非负矩阵分解(Non-negative matrix factorization，NMF)方法和脉冲耦合神经网络(Pulse Coupled Neural Network，PCNN)方法等(Sheng Zheng，2008;吴俊政等，2010;颜建军等，2007;李美丽等，2010)。根据本实验室课题项目的要求，本文结合Curevelet多尺度变换和NMF的特点，提出了一种多光谱图像和全色图像的融合方法。多光谱遥感图像保留了较多的光谱信息，但在空间细节信息上有所欠缺，而全色图像可弥补图像的空间细节信息，两种源图像互补，融合出具有较高的空间分辨率和光谱特性的融合图像。

1 非负矩阵分解

本小节仅对 Lee等(1999，2000)提出的 NMF理论和在图像处理中的应用做简单论述。

非负矩阵分解是一种在矩阵元素为非负的前提下对其进行分解的算法，即 NMF(Lee et al.，1999)。其非负性的特点非常适用于很多现实应用，如图像像素值的非负性、文本单词统计数目的非负性等。其理论可描述为:已知一个非负矩阵V，对其进行非负分解，得到一个n×r的W矩阵和一个r×m的H矩阵，使得:

其中r满足(n+m)r＜mn。在图像处理中，可将一幅图像的像素值按照行优先的方式存储为一个列向量中，则i(i≥2)幅图像组成一个含有i个列向量的数据向量集Vn×m。其中m=i，n为一幅图像中像素数量，Vn×m可以表示为:

图像质量的退化模型为:

其中V为观测图像，W为标准图像，ε为噪声信息。其运用于图像融合问题可看成是:将原始数据构成的V矩阵分解为包含特征基的向量W和权重系数H，从V中恢复出标准图像W。当r取值1时，得到唯一的特征基，它包含了原始数据的整体特征，可用于源图像的近似再现且有效抑制背景噪声(张素文等，2008)。

2 第二代Curvelet变换

2.1 Curvelet变换理论研究进展和现状

Curvelet变换是近年来常用的一种多尺度分析方法，最早的第一代 Curvelet变换是1999年由Candes和Donohot提出，它提供了稳定的、高效的和近乎最优的表示。在2-D情况，当图像具有奇异曲线且是二次可微的，则Curvelet可以自适应地“跟踪”奇异曲线。在2002年，Candes等人提出了新的Curvelet框架体系，称为第二代Curvelet变换。随后在2005年提出了两种基于第二代Curevelet变换理论的快速离散实现方法，分别是 USFF(Unequispaced FFT)算法和Wrap(Wrapping-based transform)算法。本文实验所采用的算法是Curvelet工具箱中的Wrap算法，下面对其算法求解过程做简单介绍。

2.2 基于Wrapping的快速离散Curvelet变换实现方法

算法的前期理论基础论述请有兴趣的读者参考相关文献，这里仅给出算法的过程。Wrap算法的核心思想是围绕原点Wrap，在具体实现时对任意区域，通过周期化技术一一映射到原点的仿射区域(Candès et al.，2004，2005)。具体步骤如下:

(1)对于给定的一个笛卡尔坐标下的二维函数进行2D FFT变换，得到二维频域表示:

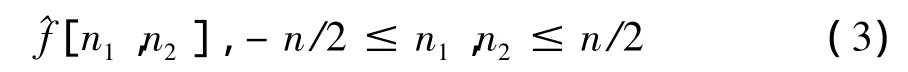
(2)在频域，对于每一对(j，l)(尺度，角度)，重采样得到采样［n1，n2］值，

Optimization of Spreader Path for Container Yard Crane

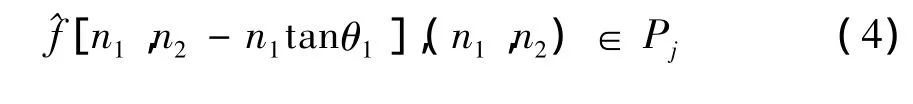
(3)将内插后的与窗函数相乘可得到，

经过变换后得到的C{j}{l}(k1，k2)结构的系数，j表示尺度，l表示方向，(k1，k2)表示 j尺度层上第l方向的矩阵坐标。

2.3 Curvelet变换的图像特征

Curvelet变换能将图像变换到不同分解层，不同方向的频带上，其不同的频带都包含了不同特征和细节信息。若分解的层次为六层，对原始图像进行Curvelet变换，然后分别保留单层系数，其余各层系数置零，进行重构，可得到图1各层的系数。

图1 Curvelet变换各层系数Fig.1 The different frequency coefficients of Curvelet

从图1中，可以看出Corase层是低频系数，包含了图像的近似图像;Detail层是中高频系数，主要包含了多个方向边缘特征信息;Fine层是高频系数，体现了图像的细节、边缘特征。

3 基于NMF和Curvelet的遥感图像融合方法

根据2.3节所述Curvelet变换的特征，设计了本文的算法，首先对多光谱图像和全色图像做Curvelet变换得到不同的频带系数，由于Corase尺度层(低频系数)能反映图像的概貌，所以分别将多光谱图像各个波段的Corase系数与全色图像的Corase系数构建初始矩阵V，对其进行非负矩阵分解，提取出各波段的特征基(考虑r=1)作为融合图像的低频系数;其次对Detail和Fine尺度层(高频系数)采用方差为测度参数进行3×3(或5×5)邻域融合;最后进行Curvelet逆变换得到最终融合图像。其算法的流程如图2所示:

图2 基于NMF+Curvelet的算法流程Fig.2 Schematic diagram for NMF+Curvelet image fusion method

(1)对已配准的多光谱图像各个波段和全色图像分别进行Curvelet分解。分别得到两种源图像的 变 换 系 数和表示多光谱图像第i个波段的低频子带系数k2)表示其高频子带系数，j表示当前分解级数，l表示分解的方向数，k1，k2表示像素点坐标值;表示全色图像的低频子带系数，表示其高频子带系数。

(4)将各波段融合后的系数进行Curvelet逆变换，最后合成融合图像。

4 仿真实验与分析

为了验证本文算法的性能，使用MATLAB7.0进行编程，操作系统:WinXP，CPU:2.2Ghz，内存:2GB，显存:512M。实验图像为多光谱图像(3个波段)与全色图像，如图3(a)、(b)所示，图像大小256×256。对比融合方法分别为:①小波融合方法(低频采用加权平均;高频用绝对值取大优先);②Curvelet融合方法(低频采用加权平均;高频用绝对值取大优先);③本文NMF+Curvelet融合算法。各方法的融合图像如图3(c)、(d)、(e)所示。

从主观上观察图3的不同方法的融合效果，可以看出小波的图像视觉效果最差，后两者视觉效果较好。本文的算法图像在轮廓、细节信息上丰富，且保留了较好的光谱特性。

图3 原始图像和各方法融合Fig.3 Original image and the fusion images of different methods

除主观评价外，对实验结果采用两类客观评价指标，一类是反映空间细节信息的指标:方差、信息熵和清晰度;另一类反映遥感图像光谱信息的指标:扭曲度和相关系数(颜建军等，2007)。结果如表1所示。由表1可以看出:本文NMF+Curvelet方法在均值、方差、信息熵最大，清晰度略低于Curvelet方法，说明该方法在空间信息上得到了增强，优于前两者;本文方法扭曲度上最大，相关系数略大于Curvelet，表明在光谱特性上与Curvelet方法相当。

表1 融合结果比较Table1 Compare Fusion Experimental Results

5 结束语

本文提出了一种结合非负矩阵分解和第2代Curvelet多尺度变换的遥感图像融合方法，在实验中表明，该方法能较好地保留了源图像的光谱特性，并在图像的空间细节信息上有所增强。但缺点是:Curvelet变换和NMF分解数字实现比较复杂，在计算的时间上相对较长，因此实时性较弱。该方法适用于本实验室的课题内容的研究，对其他的一些特定类型或特定场景的图像融合应用值得进一步探讨。

李美丽，李言俊，王红梅，等.2010.基于NSCT和PCNN的红外与可见光图像融合方法［J］.光电工程，37(6):90-95.

吴俊政，严卫东，刘俊民，等.2010.基于曲波变换和模糊理论的遥感图像融合［J］.计算机应用，30(6):162-165.

颜建军，夏春明，郑建荣.2007.基于NMF的多光谱图像和全色图像融合方法［J］.计算机工程，33(21):169-171.

张素文，陈娟.2008.基于非负矩阵分解和红外特征的图像融合方法［J］.红外技术，30(8):446-449.

CandèsE J，DemanetL，Donoho D L.2005.Fast Discrete Curvelet Transforms［R］.Stanv，CA，USA:Applied and Computational Mathematics California Institute of Technology，1-43.

CandèsE J，DonohoD L.2004.New tight frames of curve lets and optimal representations of objects with singularities［J］.Communication on Pure and Application of Math，57(2):219-266.

Lee D D，Seung H S.1999.Learning the parts of objects by non-negative matrix factorization［J］.Nature，401(6755):788-791.

Lee D D，Seung H S.2001.Algorithms for non-negative matrix factorization［C］//Advances in Neural Information Processing Systems.Cambridge:MTT Press，(13):556-562.

Sheng Zheng，Wen-zhong Shi.2008.Remote Sensing Image Fusion U-sing Multiscale Mapped LS-SVM［J］.IEEE Transactions on Geoscience and Remote Sensing，46(5):1313-1322.