基于稀疏反演的OBS数据多次波压制方法

刘国昌，陈小宏，宋家文＊

1 中国石油大学（北京）油气资源与探测国家重点实验室，北京 102249 2中国石油大学（北京）CNPC物探重点实验室，北京 102249

1 引 言

海底地震仪OBS观测是一种将检波器直接放置于海底的地震观测系统［1］.近年研究表明，在海洋地球物理调查中，可以利用OBS探测海底地质构造、天然气水合物和游离气、海底油气资源，调查地下岩层岩性，确定海底的弹性和各向异性等物性参数［2］.在油气勘探中，由于OBS造价昂贵，成本较高，OBS站点一般分隔较远，不同于海底电缆地震勘探观测系统［3］.在海洋深水区域，海底电缆的应用受到限制，因此，OBS技术在海洋深水勘探中具有重要的作用.OBS数据和其他海洋勘探数据（拖缆数据、海底电缆数据等）一样面临着多次波干扰问题，由于海水表面反射系数大，与表层相关的多次波压制就成为OBS数据处理中最需解决的问题之一［4－5］.

多次波的压制方法主要分为两类［6－7］：一类是利用一次波和多次波的特征差异来压制多次波，统称为滤波法，如预测反褶积、抛物Radon变换等；另一类是从地震数据中预测多次波，然后将其从地震数据中减去，该类方法基于波动方程理论，也称为波动方程预测相减法，主要有：波场外推法［8］、反馈迭代法［9］、逆散射级数法［10］等.本文研究涉及的方法属于反馈迭代法的范畴.在反馈迭代方法中，SRME是经典的自由表面多次波压制方法［9］.SRME一般分为两步：多次波预测和自适应相减，在多次波与一次波同相轴相交的情况下，基于一次波能量最小假设的自适应相减方法会损伤一次波，黄新武等［7］、薛亚茹等［11］、李鹏等［12］都对该方法做过深入的研究.Berkhout（2006）将SRME理论推广到反数据域压制多次波，该方法与正数据域的SRME相比，理论表达简单，避免了自适应相减过程，因此地震记录可以完全保留有效波信息［13］.马继涛等在反数据域压制多次波理论基础上，提出了平面波域反数据压制多次波的方法，提高了矩阵求逆的稳定性和计算有效性［14－15］.Van Borselen等［16］，Biersteker［17］在反演理论基础上，通过最小能量约束研究了一次波的反演估计问题，从反演的角度避免了自适应相减的过程.van Groenestijn和 Verschuur（2009）［18］提出了EPSI方法，在稀疏约束的基础上，通过多维反演迭代求解估计一次波，该方法可以精确地估计一次波，不需要自适应相减，且计算稳定.

对于不同的地震观测方式，采用SRME的方法略有不同.马继涛等［19］在SRME理论基础上，研究了海底电缆地震数据中自由表面多次波的压制问题，得到了较好的效果.反馈迭代法需要全波场的信息，如果地震数据有缺失，需要对地震数据做插值重建处理.然而对于OBS数据，检波点非常稀疏，插值结果难以保真，因此仅仅采用OBS数据利用反馈迭代法预测多次波具有很大的局限性［3，5］.Verschuur和 Neumann（1999）［4］在 SRME 基础上，利用拖缆数据和OBS数据联合研究了OBS多次波压制问题.本文将SRME方法拓展到EPSI方法，联合海洋常规拖缆数据和OBS数据，研究OBS数据自由表面多次波压制方法.首先，详细介绍了反馈迭代自由表面多次波压制理论；然后在此基础上推导了联合拖缆数据压制OBS多次波的EPSI原理，给出了OBS多次波压制的具体步骤；最后，利用模拟数据验证了本文方法的有效性.

2 反馈迭代模型与多次波预测理论

地震数据是炮点坐标xs＝ ［sx，sy，sz］、检波点坐标xr＝ ［rx，ry，rz］和时间t的函数，将地震数据表示为d（xs，xr，t），在频率域地震数据变为d（xs，xr，ω）.省略炮点和检波点坐标，某一频率切片的地震数据可以用矩阵D表示.地震数据可以表示为一次波（指除了自由表面多次波之外的波场信息，即包含层间多次波）和自由表面多次波的和

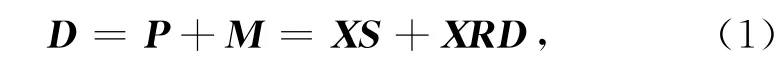
其中，P表示一次波，M表示多次波，X为一次波脉冲响应，S为震源矩阵，R为表面反射系数矩阵.通过公式（1），可以推导出压制多次波的三种反馈迭代方法.

（1）SRME方法.由公式M＝XRD，可以看出，表面相关多次波可以通过地震数据D作用算子XR预测得到.因此有M＝PS－1RD，S－1R是表层相关算子，通过迭代法就可以预测多次波模型，然后利用自适应相减方法消除掉S－1R的影响，这就是经典的SRME方法.

（2）反数据域方法.公式（1）可以写成 （IXR）D＝XS，那么

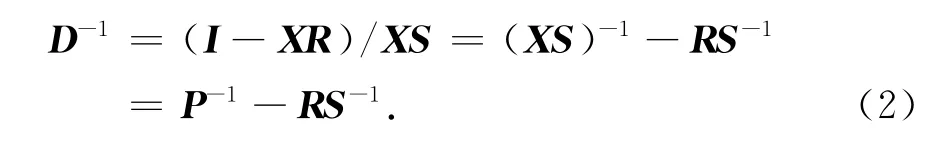
由于表层相关算子RS－1不含有任何与时间相关的信息，在反数据域是一个位于零时间附近聚焦点，因此在反数据域地震数据变成一次波加上表面相关算子，在时间域可以通过切除零时间附近的表面相关算子，从而得到一次波的估计.该方法需要做矩阵的逆运算，因此需要采用稳定的矩阵求逆方法.

（3）EPSI方法.SRME方法需要自适应相减，反数据域方法在频率域矩阵求逆存在不稳定性问题，而EPSI方法很好地解决了这些问题，该方法直接从方程（1）入手，对时间域一次波脉冲响应施加稀疏约束，采用迭代反演的方法估计一次波与多次波.假设自由表面反射系数为－1，那么方程（1）中的R＝－I.采用Claerbout对优化问题的描述方式［20］，EPSI方法可以描述成下面的优化问题：

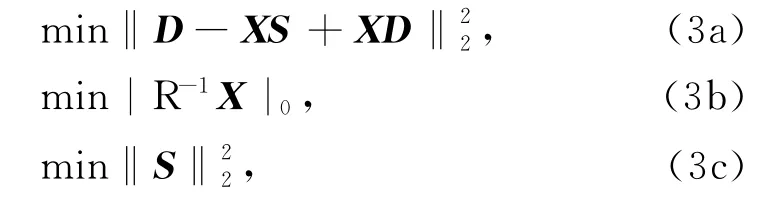
其中‖A‖表示对矩阵A所有元素求平方和，｜A｜0表示A的L－0范数.公式（3a）是由公式（1）得到的，采用L－2范数最小描述公式（1）两端的能量差最小；公式（3b）表示时间域一次波脉冲响应是稀疏的，采用零范数最小描述其稀疏性，R－1表示是对所有频率切片的X做逆Fourier变换；公式（3c）表示满足震源特性S的能量最小，采用L－2范数描述.由于Fourier变换满足能量守恒性质（Parseval定理），公式（3a）和（3c）中的L－2范数问题在频率域求解与时间域求解是等同的，而公式（3b）中的L－0范数需要在时间域中求解.可以看出，公式（3）中需要求解的变量有两个：一次波脉冲响应X和震源特性S，其他均是已知量.由于存在零范数问题，该优化问题是非线性问题，不能直接采用共轭梯度迭代法求解，van Groenestijn和 Verschuur（2009）［18］在迭代过程中结合零范数约束利用最速下降法求解上述问题.时间域X的稀疏约束问题还可以采用其他的稀疏约束方法，比如 Lin和 Herrmann等［21］提出的curvelet域稀疏约束的EPSI方法，就是利用curvelet变换的稀疏特性，假设一次波在curvelet域中具有稀疏的特性来估计一次波，但是curvelet变换稀疏约束估计一次波需要较大的计算量.

3 联合拖缆数据压制OBS多次波的EPSI方法

上述EPSI方法是针对常规观测系统地震数据的方法，要求检波点与炮点位于同一观测平面上，且只用一个数据体.而OBS数据观测方式不同于常规观测方式，检波点稀疏且放置于海底，炮点和检波点并不位于同一观测平面上，因此本文研究联合拖缆数据压制OBS多次波.图1显示了OBS波场传播示意图，可以看出，OBS接收到的表面相关多次波（包括上行波场和下行波场）都可以看作是拖缆采集数据Dsur与OBS一次波脉冲响应Xobs的多维褶积，因此我们将公式（1）改写为

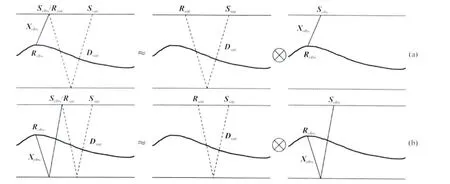
图1 OBS波场传播示意图（a）OBS下行波场中的多次波示意图；（b）OBS上行波场中的多次波示意图.左：OBS多次波；中：拖缆采集数据Dsur；右：OBS一次波（包括直达波）脉冲响应Xobs.Fig.1 The sketch map of OBS wavefields（a）OBS downgoing wavefield；（b）OBS upgoing wavefield.Left：OBS multiples；middle：streamer data Dsur；right：the primary（including direct wave）impulse response of OBS data Xobs.

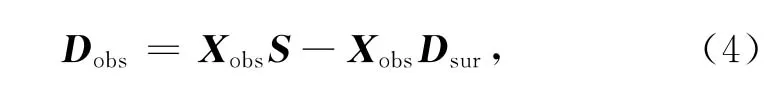
其中，Dsur是常规拖缆数据，Dobs是OBS数据，Xobs是OBS一次波脉冲响应，S是震源矩阵.在计算过程中，由于OBS数据检波点非常稀疏，我们仅仅需要在共检波点道集上压制多次波，对某一共检波点道集来说，Dobs和Xobs是一维向量，Dsur是拖缆数据的二维矩阵.在采集过程中，拖缆和OBS数据一般采用同样类型的震源，因此这里假设震源特性S是不变的.公式 （4）与公式（1）的差别是公式（4）含有拖缆数据和OBS数据两个数据体，但求解过程与公式（1）近似.类似于公式（3），我们将公式（4）写成下面的优化问题

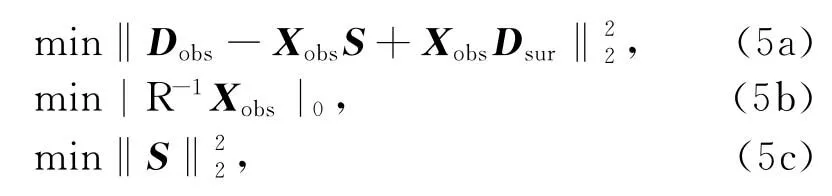
类似于van Groenestijn和 Verschuur（2009）［18］给出的公式（3）的求解方法，这里我们给出公式（5）的详细求解方法.

（1）首先，确定Xobs及其梯度 ΔXobs.将公式（5a）写成目标函数的形式

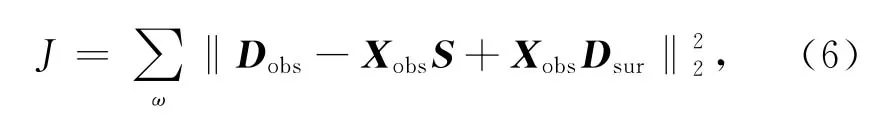
对上述目标函数求导得到Xobs的梯度

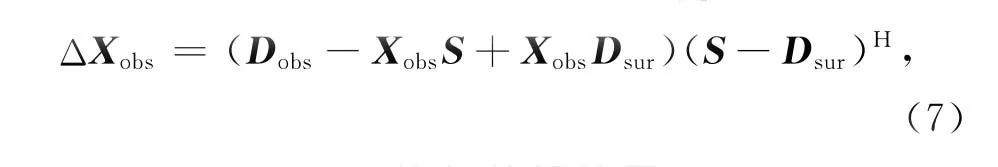
其中 （·）H表示 （·）的复共轭转置，Dobs－XobsS＋XobsDsur是残差项.（Dobs－XobsS＋XobsDsur）SH的作用是将残差中的OBS一次波信息转化为OBS一次波脉冲响应，而 （Dobs－XobsS＋XobsDsur）DsurH的作用是将残差中的OBS多次波信息转化为OBS一次波脉冲响应.如果迭代初始值设为：X（0）obs＝0，S（0）＝0，那么经过一次迭代的ΔXobs结果是OBS数据与拖缆数据的多维相关，即

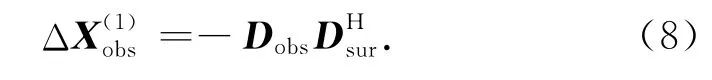
（2）其次，满足时间域Xobs的稀疏性.为了采用稀疏约束，van Groenestijn和 Verschuur（2008）［22］研究了直接对X加稀疏约束的方法，结果表明反演收敛速度非常慢.为了提高计算效率，van Groenestijn和 Verschuur（2009）［18］将稀疏约束加到X的更新项ΔX上.类似地，本文将约束加到OBS一次波脉冲响应更新项ΔXobs上.具体做法是将ΔXobs变换到时间域，选择一个时间窗口，在时间窗口内保留一个或者几个时间域ΔXobs的最大值，其他设为零，该最大值代表了时间域的同相轴，这样保证了ΔXobs在时间域同相轴的个数比较少，从而满足了稀疏性.随着迭代次数的增加，选择的时间窗口依次增大以保证迭代能够收敛，然后将稀疏的ΔXobs加到一次波脉冲响应上，得到一次波脉冲响应下一次迭代的结果

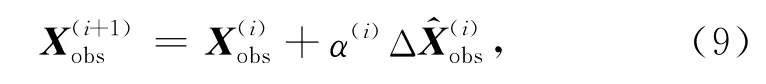
其中i，j是矩阵坐标，“·＊”表示矩阵元素对应相乘.第一次迭代的时间窗口选取要适当，不能将多次波同相轴包括进来参与计算.随着迭代次数的增加，残差里面浅层一次波及其产生的多次波能量已经被减掉了，这有助于估计深层的弱一次反射.

（3）最后求解震源特性S.震源特性可以在时间域通过匹配得到，也可以通过频率域的除法得到.

至此，已经得到迭代一次后的一次波脉冲响应Xobs和震源特征S，通过多次迭代即可得到最终结果.估计的一次波可以直接通过Xobs和S的乘积得到

也可以采用保守的方法，即从原始数据中减去估计的多次波

通过少量的迭代计算浅层对应的多次波就能够估计出来，而深层产生的多次波能量非常弱，因此在精度要求不高的情况下，可以用较少的迭代运算来估计多次波，然后采用保守方法计算一次波，从而提高计算效率.对于海底地震仪不同分量（压力和X，Y，Z分量）的数据，可以分别利用EPSI估计各分量数据中的一次波.本文算例以压力分量为例说明EPSI压制OBS多次波的方法.

4 模型算例

用一个模拟的OBS数据压力分量和拖缆数据说明本文提出算法的有效性.图2a是速度模型，图2b是模拟的OBS共检波点道集，由于炮点和检波点不在同一平面上，因此直达波具有双曲线形态.为便于比较，这里也给出了吸收边界条件下模拟的不含表面相关多次波的记录（图2c）.图3是模拟的拖缆数据.比较图2b和图2c可以看出OBS数据多次波干扰非常严重，尤其在深层部分，一次波能量几乎被多次波淹没，例如箭头所指的第四个反射界面，一次波和多次波几乎完全重合，对于这样的同相轴SRME自适应相减会有很大的局限性.

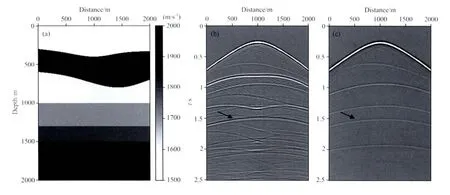
图2 （a）速度模型；（b）自由表面模拟的OBS数据；（c）吸收边界条件模拟的OBS数据Fig.2 （a）Velocity model；（b）Synthetic OBS data with free－surface boundary conditions；（c）Synthetic OBS data with absorbing boundary conditions

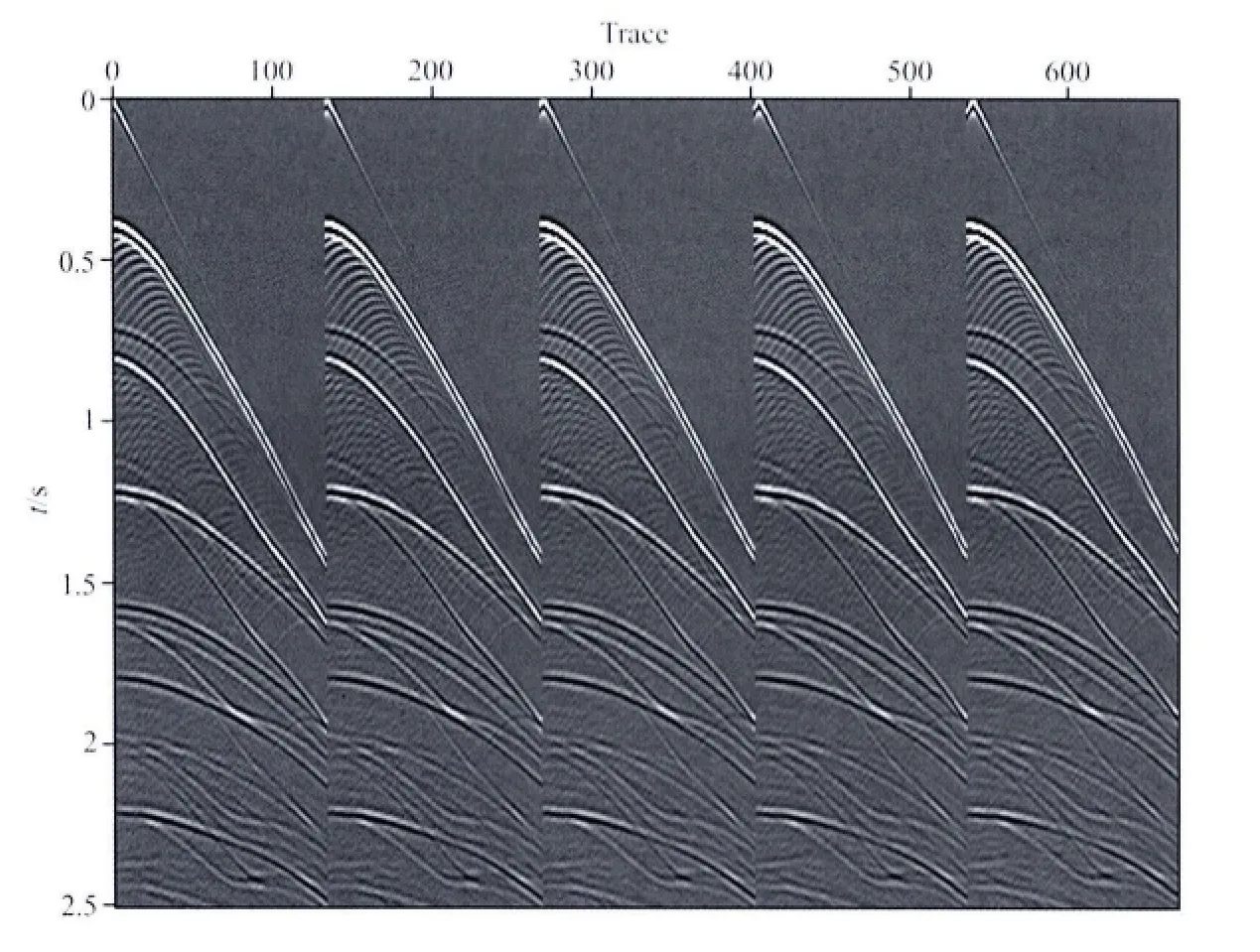
图3 模拟的拖缆数据（前5炮数据）Fig.3 Synthetic streamer data（first five shot gathers）

图4—图7显示了EPSI方法迭代的结果.随着迭代次数的增加，浅层的梯度逐渐衰减，说明在迭代过程中选择时间窗口应逐渐变大，这样才能把新的一次波能量包含进来（图4）.从图5可以看出，一次波脉冲响应随着迭代次数的增加，逐渐地被反演出来，当迭代10次时，浅层的一次波脉冲响应已经被反演出来，由于时间窗口还没有达到深层对应的时间，因此深层的一次波脉冲响应没有被反演出来.正是由于迭代过程是从浅层到深层逐步地估计一次波，所以保证了一次波和多次波能够很好的预测和分离.从EPSI估计得到的一次波数据（图6c）可以看出EPSI得到的一次波非常清晰，很好地保持了有效信号.图7给出了估计的多次波随着迭代次数的变化情况，随着迭代次数的增加，与深层有关的多次波逐渐被反演出来，由于深层有关的多次波能量非常弱，第一次迭代的结果（图7a）就能够反映主要的多次波能量.注意箭头所指的深层有关的多次波能量，在第一次迭代结果中并没有被估计出来，随着迭代次数的增加它被很好地估计出来了.由于深层有关的多次反射波能量很弱，利用EPSI方法时，可以选用较少的迭代次数得到多次波，然后根据公式（12）得到一次波，这样可以提高计算效率，当然也会降低计算精度.最后比较EPSI、SRME自适应相减和吸收边界条件模拟得到的一次波记录（图8）.这里SRME自适应相减采用的是非稳态自回归自适应相减方法［23］，该方法充分考虑了子波的时变性.从图8可以看出SRME方法由于深层多次波和一次波相交比较严重，效果较差，第四个反射轴与多次波几乎完全重合，SRME自适应相减将其当作多次波能量直接减掉了，第五个反射轴处多次波同相轴非常复杂，SRME自适应相减结果也不理想.而EPSI方法可以很好地估计一次波，与吸收边界条件模拟得到的一次波记录非常相近，充分说明EPSI方法可以很好地压制OBS数据中的多次波.

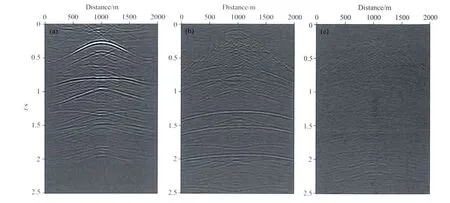
图4 不同迭代次数的梯度ΔXobs（a）迭代1次；（b）迭代10次；（c）迭代20次.Fig.4 The gradientΔXobsduring different iterations（a）Iterations i＝1；（b）Iterations i＝10；（c）Iterations i＝20.

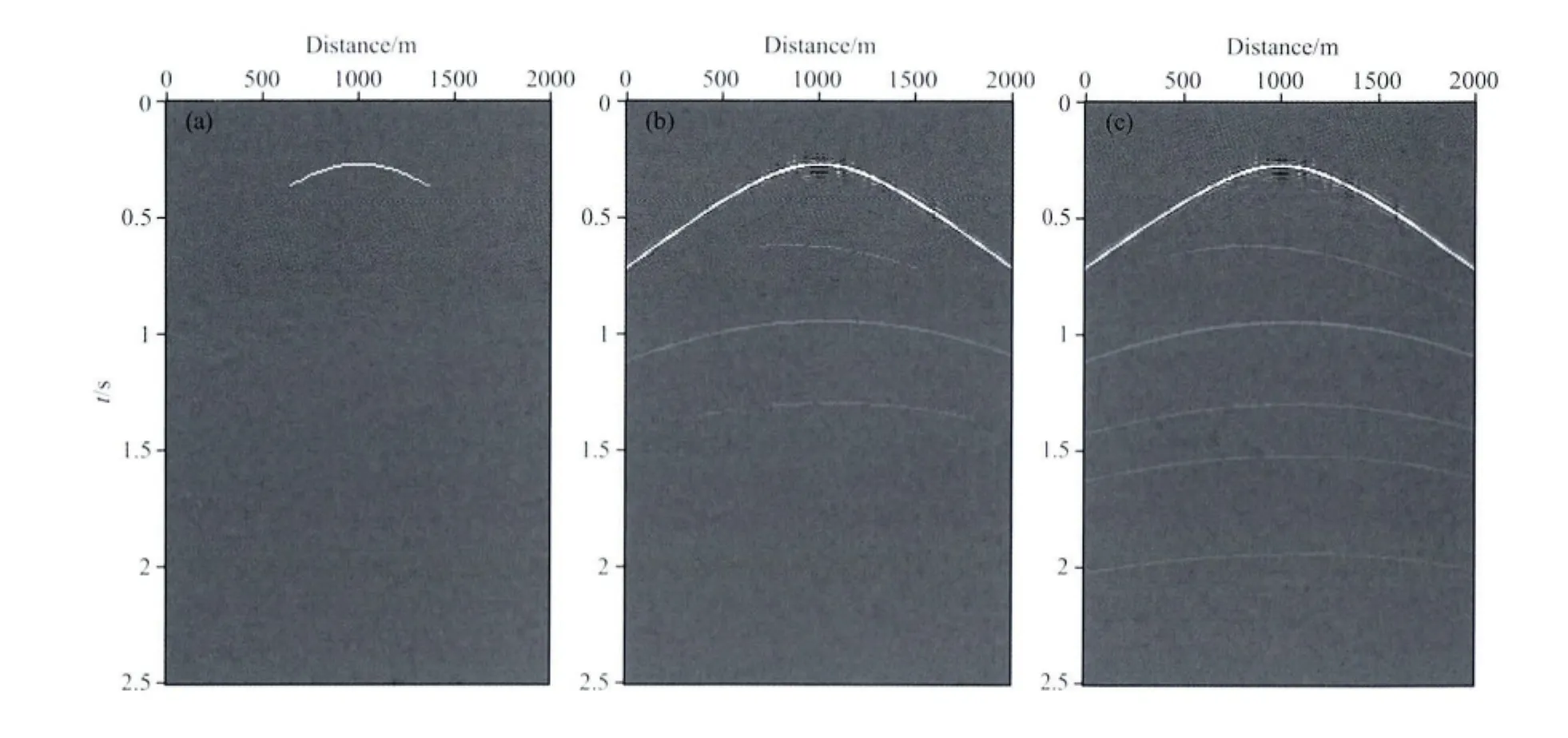
图5 不同迭代次数的一次波脉冲响应Xobs（a）迭代1次；（b）迭代10次；（c）迭代20次.Fig.5 The primary impulse response Xobsduring different iterations（a）Iterations i＝1；（b）Iterations i＝10；（c）Iterations i＝20.

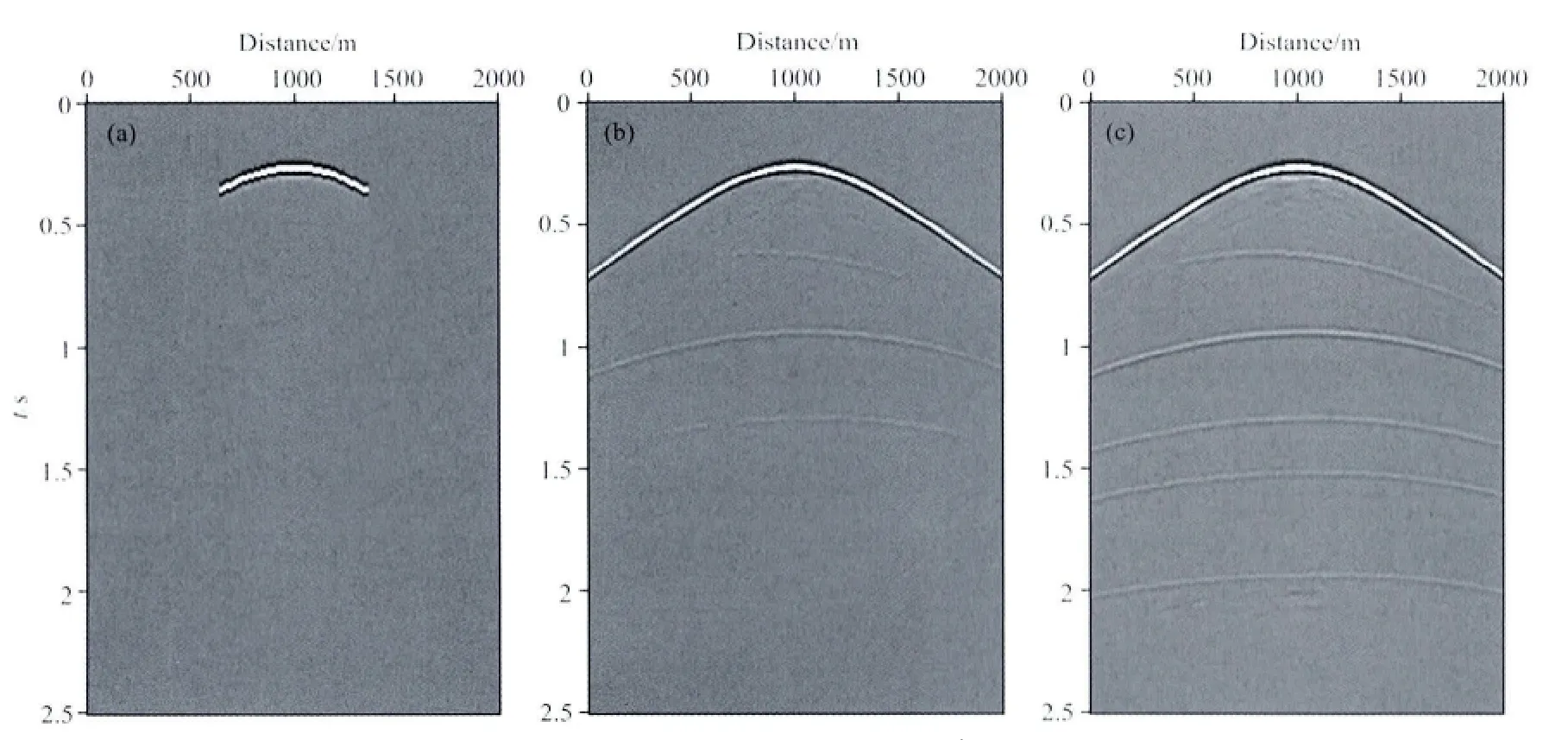
图6 不同迭代次数估计的一次波数据obs＝XobsS（a）迭代1次；（b）迭代10次；（c）迭代20次.Fig.6 The estimated primaries XobsSduring different iterations（a）Iterations i＝1；（b）Iterations i＝10；（c）Iterations i＝20.

图7 不同迭代次数估计的自由表面多次波数据XobsDsur（a）迭代1次；（b）迭代10次；（c）迭代20次.Fig.7 The estimated multiples XobsDsurduring different iterations（a）Iterations i＝1；（b）Iterations i＝10；（c）Iterations i＝20.

在OBS偏移成像过程，由于检波点鬼波数据有较大的照明范围，常常用来做镜像偏移［5］，这时需要用到检波点鬼波信息，在图8得到的一次波记录中不含有检波点鬼波信息.为了得到含有检波点鬼波信息的一次波记录，首先需要将OBS数据中的直达波（图9a中虚线以上的部分）切除作为EPSI的输入数据.图9c显示的多次波是不含有检波点鬼波的记录，通过上下行波的分离可以用于OBS数据镜像偏移.

5 结论与讨论

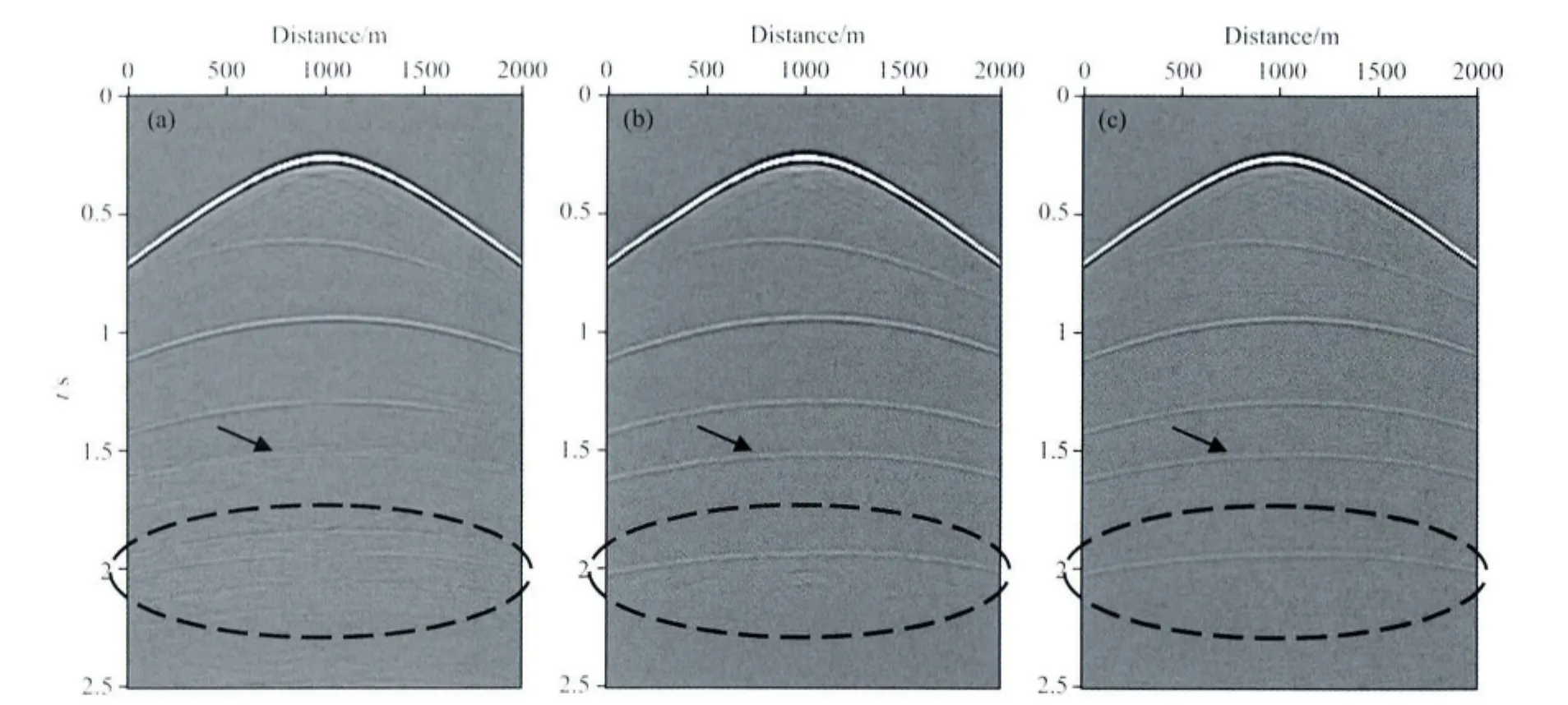
图8 不同方法得到的一次波结果比较（a）SRME自适应相减；（b）EPSI方法由公式（11）得到的一次波；（c）EPSI方法由公式（12）得到的一次波.Fig.8 The comparison of obtained primaries between different methods（a）SRME；（b）EPSI by Eq.（11）；（c）EPSI by Eq.（12）.

文中介绍了压制多次波的反馈迭代模型及其衍生的三种方法：经典SRME方法、反数据域方法和EPSI方法.EPSI方法与其他反馈迭代法一样是一种完全数据驱动的方法，不需要地下介质的任何信息.但EPSI与SRME不同，EPSI方法不需要自适应相减步骤，在稀疏约束基础上直接反演估计一次波信息，从而保护了一次有效波反射信息；EPSI与反数据域方法不同，EPSI方法不需要考虑矩阵求逆的稳定性问题，采用矩阵乘法的迭代计算估计一次波.OBS数据采集具有自己的特点，与海底电缆数据不同，海底电缆数据一般检波点较多，可以只用海底电缆数据本身预测和估计一次波，而OBS数据检波点非常稀疏，本文充分考虑了OBS采集的特点，以EPSI方法为理论基础，提出了联合拖缆数据压制OBS多次波方法，利用拖缆数据的信息克服了稀疏检波点OBS多次波预测的困难.模拟算例验证了本文方法的有效性.

EPSI方法需要大量的矩阵乘法运算，计算量较大，但由于OBS数据量相对较少，计算量可以接受.另外，为了提高计算效率可以采用较少的迭代次数，利用公式（12）保守方法估计一次波，这样，在满足精度的要求下可以提高计算效率.本文采用时间域L－0范数稀疏约束的EPSI方法估计OBS一次波，还可以将其扩展到利用其他稀疏变换（如curvelet变换，seislet变换等）稀疏约束的EPSI方法，发展利用其他稀疏变换的EPSI方法压制OBS多次波是下一步的研究方向.

致 谢 感谢马继涛博士对SRME和反数据域压制多次波方法的有关讨论，感谢荷兰Delft理工大学的Verschuur博士的指导和国家留学基金委的资助.

（

）

［1］ Moghaddam P，Libak A，Keers H，et al.Efficient and accurate modeling of ocean bottom seismometer data using reciprocity.Geophysics，2012，77（6）：T211－T220.

［2］ 阮爱国，初凤友，孟补.海底天然气水合物地震研究方法及海底地震仪的应用.天然气工业（地质与勘探），2007，27（4）：46－48.Ruan A G，Chu F Y，Meng B.Seismic methods and OBS application in the study of oceanic gas hydrates.NaturalGas Industry（in Chinese），2007，27（4）：46－48.

［3］ Dash R，Spence G，Hyndman R，et al.Wide－area imaging from OBS multiples.Geophysics，2009，74（6）：Q41－Q47.

［4］ Verschuur D J，Neumann E I.Integration of OBS data and surface data for OBS multiple removal.SEGTechnical ProgramExpandedAbstracts，1999：1350－1353.

［5］ Pica A，Manin M，Granger P，et al.3DSRME on OBS data using waveform multiple modeling.SEGTechnicalProgram ExpandedAbstracts，2006：2659－2663.

［6］ Weglein A B.Multiple attenuation：an overview of recent advances and the road ahead.TheLeadingEdge，1999，18（1）：40－44.

［7］ 黄新武，孙春岩，牛滨华等.基于数据一致性预测与压制自由表面多次波——理论研究与试处理.地球物理学报，2005，48（1）：173－180.Huang X W，Sun C Y，Niu B H，et al.Surface－related multiple prediction and suppression based on data－consistence：A theoretical study and test.ChineseJ.Geophys.（in Chinese），2005，48（1）：173－180.

［8］ Sava P，Guitton A.Multiple attenuation in the image space.Geophysics，2005，70（1）：V10－V20.

［9］ Verschuur D J，Berkhout A，Wapenaar C.Adaptive surface related multiple elimination.Geophysics，1992，57（9）：1166－1177.

［10］ 李翔，胡天跃.逆散射级数法去除自由表面多次波.地球物理学报，2009，52（6）：1633－1640.Li X，Hu T Y.Surface－related multiple removal with inverse scattering series method.ChineseJ.Geophys.（in Chinese），2009，52（6）：1633－1640.

［11］ 薛亚茹，陈小宏，陆文凯.压制多次波的正交多项式谱减法.地球物理学报，2009，52（3）：817－823.Xue Y R，Chen X H，Lu W K.Orthogonal polynomial spectrum subtraction for multiple attenuation.ChineseJ.Geophys.（in Chinese），2009，52（3）：817－823.

［12］ 李鹏，刘伊克，常旭等.均衡拟多道匹配滤波法在波动方程法压制多次波中的应用.地球物理学报，2007，50（6）：1844－1853.Li P，Liu Y K，Chang X，et al.Application of the equipoise pseudomultichannel matching filter in multiple elimination using wave－equation method.ChineseJ.Geophys. （in Chinese），2007，50（6）：1844－1853.

［13］ Berkhout A J.Seismic processing in the inverse data space.Geophysics，2006，71（4）：A29－A33.

［14］ Ma J T，Sen M K，Chen X H.Free－surface multiple attenuation using inverse data processing in the coupled planewave domain.Geophysics，2009，74（4）：V75－V81.

［15］ 马继涛，Sen M K，陈小宏.平面波域反数据处理压制多次波方法研究.地球物理学报，2009，52（3）：808－816.Ma J T，Sen M K，Chen X H.Multiple attenuation using inverse data processing in the plane－wave domain.ChineseJ.Geophys.（in Chinese），2009，52（3）：808－816.

［16］ van Borselen R G，Fokkema J T，van den Berg P M.Removal of surface－related wave phenomena—the marine case.Geophysics，1996，61（1）：202－210.

［17］ Biersteker J.Magic：Shell′s surface multiple attenuation technique.SEGTechnicalProgramExpandedAbstracts，2001：1301－1304.

［18］ van Groenestijn G，Verschuur D.Estimating primaries by sparse inversion and application to near－offset data reconstruction.Geophysics，2009，74（3）：A23－A28.

［19］ 马继涛，Sen M，陈小宏等.海底电缆多次波压制方法研究.地球物理学报，2011，54（11）：2960－2966.Ma J T，Sen M，Chen X H，et al.OBC multiple attenuation technique using SRME theory.ChineseJ.Geophys.（in Chinese），2011，54（11）：2960－2966.

［20］ Claerbout J F.Image estimation by example：Geophysical soundings image construction.Stanford Exploration Project，2012，available on http：／／sep.stanford.edu／sep／prof／.

［21］ Lin T， Herrmann F. Estimating primaries by sparse inversion in a curvelet－like representation domain.The 73rd Conference and Exhibition，EAGE，Extended Abstracts，2011.

［22］ van Groenestijn G，Verschuur D.Towards a new approach for primary estimation.SEGTechnicalProgramExpanded Abstracts，2008：2487－2491.

［23］ Fomel S.Adaptive multiple subtraction using regularized nonstationary regression.Geophysics，2009，74：V25－V33.