基于非正交网格的带地形三维瞬变电磁场模拟
邱稚鹏,李展辉,李墩柱,黄清华*
1 北京大学地球与空间科学学院地球物理学系,北京 100871
2 美国加州理工学院地球与行星科学系,美国加州帕萨蒂纳 91125
1 引 言
在野外瞬变电磁(Transient electromagnetics,TEM)的测量过程中,测区的地形不可避免地存在起伏,有时甚至起伏很剧烈.这就导致实际的测量数据除包含地下结构的有效信息之外,还会掺杂着地形的影响.考察地形对瞬变电磁场影响的正演模拟对实际测量、反演方法的研究以及测量数据的解释有着重要的指导意义.
现有的关于瞬变电磁正演的研究包括有限元法(Finite-element method,FEM)[1-5]、积 分 方 程 法(Integral equations method,IEM)[6-10]、时域有限差分(Finite difference time domain,FDTD)方法[11-22]等,其中,带地形瞬变电磁场正演模拟的研究相对较少[1-2,6-9,12-14].FEM 进行带地形 TEM 三维正演 时 可以很好地刻画地形,但其求解的过程需要解大型矩阵,耗费大量时间.IEM的主要计算量与异常体或地形的规模、形状有关,当地形较简单时,IEM的计算量很小,可以高效地进行计算.但若要计算较为复杂的地形时,IEM会明显受到限制.
Hohmann与Wang[15]提出了一种基于修正的Du Fort-Frankel格式[18]的有限差分法,该方法可以显式地得到任意时间点的电磁场分量;但他们没有考虑如何计算带地形情况下的电磁场.Endo与Noguchi[12]提出了垂向网格变换算法,通过将带地形的物理域的场映射到平坦的计算域,实现了对地形的近似;该算法在地表采用向上延拓作为边界条件,但在地形起伏较大时并不能获得准确的边界条件;该文还计算了简单地形起伏的TEM场,但计算区域比较小,模型的设计仅限于单一模型.Mitsuhata[1]利用有限元法分析了二维长偏移距瞬变电磁法(Long offset TEM,LOTEM)在电偶源激发的情况下地形的影响,认为对于远离地形的测点,地形的影响不显著.唐新功等[6-9]利用积分方程法进行的LOTEM数值模拟表明,在电偶源情况下,地形的影响是一种“本地”的影响,并建议实际测量时选择较平坦或开阔的地形[8];但该方法对地形刻画采用的是阶梯近似,所以其地形刻画比较粗糙.李墩柱[14]将非正交网格算法[19-20]引入到瞬变电磁场中,在地表引入了空气层,避免了地形起伏给向上延拓带来的问题;该算法在由逆变分量计算协变分量时,采用某点周围四个点的等权投影的平均来近似该点的对应分量,当网格的划分存在一定梯度时,该近似可能带来一定的误差.本文针对李墩柱算法中存在的上述问题,提出了一种采用非等权投影的改进算法,在一定程度上提高了该算法的精度.
总体上讲,以往针对地形影响的研究大都局限于对山峰、山谷、斜坡等地形类型的简单分析,对决定地形影响效果的各种因素的讨论并不充分.为此,本文利用我们改进的非正交网格算法开展了瞬变电磁场的数值模拟研究,探讨了地形的深度、宽度和相对源的距离等参数对瞬变电磁场的影响,获得了一些初步认识.
2 非正交网格FDTD
2.1 非正交网格
空间中的任意矢量都可以按照非正交的一般坐标系(图1)进行展开.若选取该坐标系的三分量作为基矢量,则可以得到任意矢量的展开式(以电场为例):
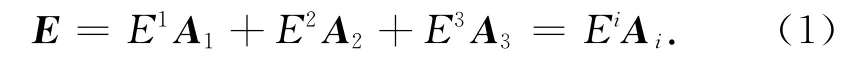

图1 一般坐标系逆变基矢量与协变基矢量[20]Fig.1 Covariant vectors and contravariant vector in a general coordinate system[20]
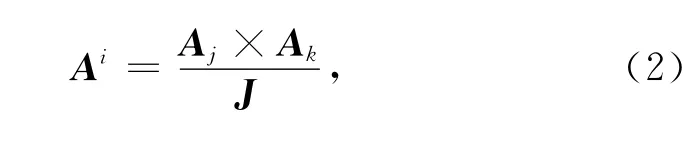
其中,
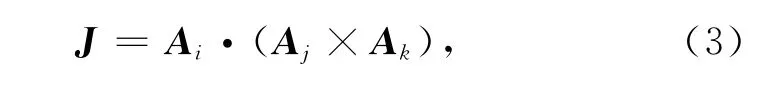
协变基与逆变基有如下关系:
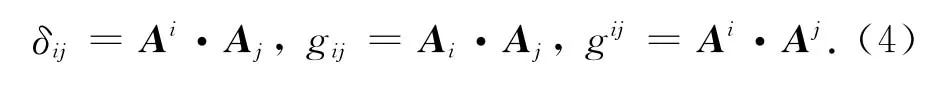
gij与gij称为度量张量的分量.
同样的,任意矢量也可对逆变基矢量进行展开.将协变基定义为非正交网格的棱,则该坐标系中线积分与面积分可分别表示如下:
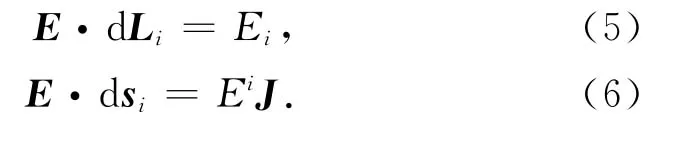
2.2 非正交网格FDTD
对于麦克斯韦方程组,散度方程可以利用边界条件自然满足,实际计算中主要是对两个旋度方程进行计算.网格的划分采用Yee网格[21],电场定义在网格的棱心和整数时间点上,磁场各分量定义在
在非正交坐标系中,相应于上述协变基矢量Ai,存在一套相应的逆基,称为逆变基矢量Ai,其定义如下:网格的面心和半整数时间点,考察积分形式的安培定律和法拉第定律,在各向同性的情况下可以表示为:
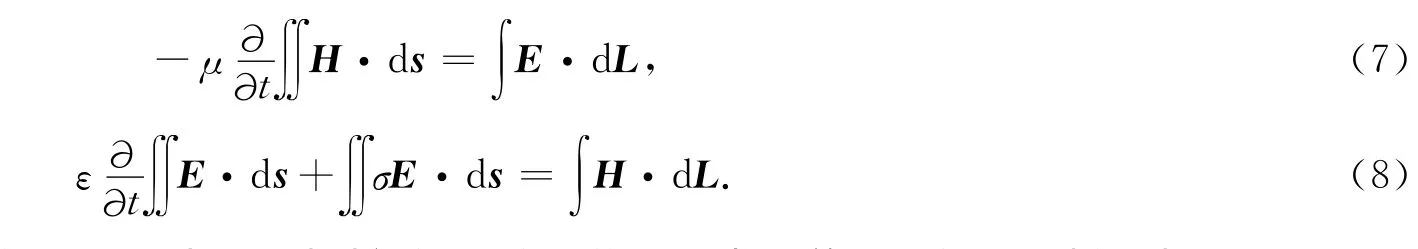
将式中的线积分和面积分利用式(5),(6)表示.对时间的一阶导数采用中心差分近似,可以得到
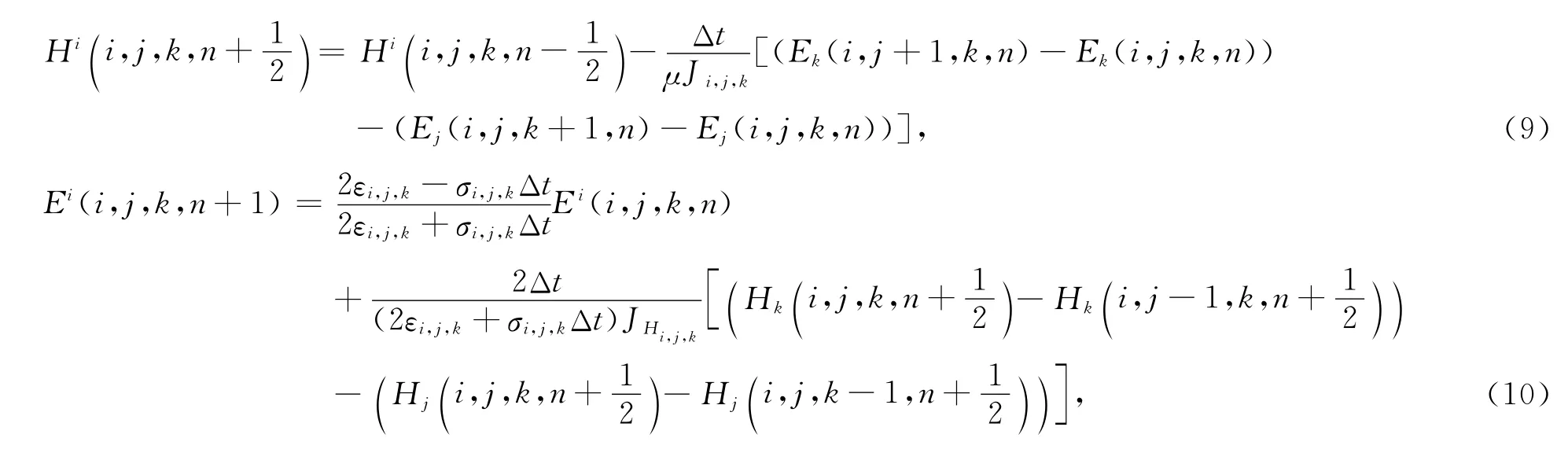
其中,Ji,j,k,JHi,j,k分别表示电场和磁场相应位置协变基矢量围成的晶格体积.最后,为完成电场与磁场的迭代,需要将等式左边的电场与磁场的逆变分量转换为协变分量.考虑到Yee网格的任意点只定义了一个分量,相应的另外两个分量需要由该点周围点的分量平均近似得到[14]:
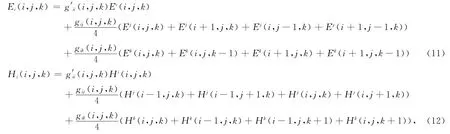
其中g′ii=Ai·AHi.Ai,AHi分别表示电场与磁场相应位置的基矢量.非正交网格的稳定性条件为[20]:
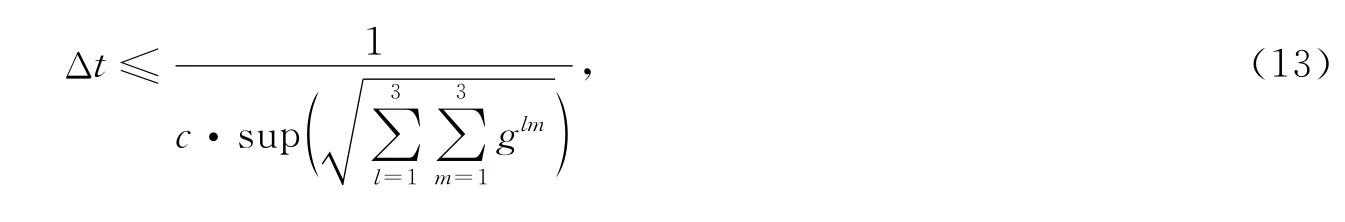
其中,sup代表上限(upper-bound).
同时,因为瞬变电磁场近似为扩散场,为了保证方程中的波动不会影响到扩散项,还需要保证最大时间步长[15]:

其中α的选取一般小于0.2.
2.3 改进的非正交网格FDTD
在上一小节介绍的非正交网格FDTD方法中,由逆变分量计算协变分量时,不同方向分量间的投影采用了等权投影作为近似.这在网格的划分存在梯度时,可能带来一定的误差.为此,本文进行以下改进,将上述等权投影改为相应位置实际的不等权投影,即通过每一点场的分量乘以相应位置上的度量张量来计算相应的投影,从而减小在带地形模型中由于网格划分存在梯度所带来的误差.这样,式(11)、(12)可修正如下:
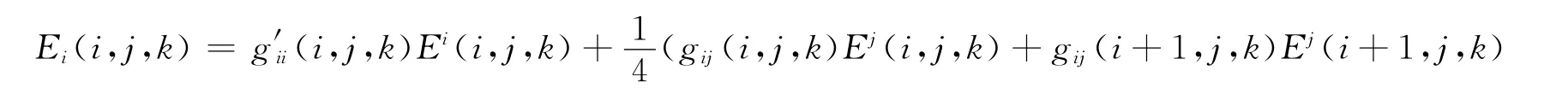
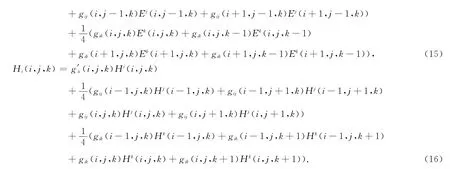
2.4 初始条件与边界条件
在本文数值模拟中,采用磁偶极子源作为激励源,便于与相应的理论解进行对比检验.为避免磁偶极子源的奇异性,数值模拟中常使用某一时刻的初始场来代替源的影响.模拟脉冲信号下的电磁场,在柱坐标下,磁矩为M的磁偶极子产生的电场的阶跃响应为[22]
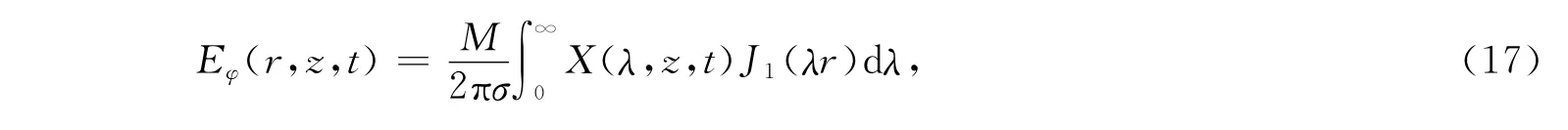
其中,
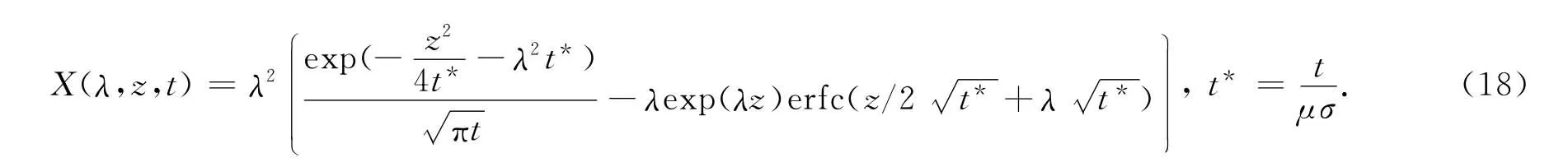
对式(17)求t的一阶数值导数即可以得到电场的初始响应,再求旋度即可得到磁场的初始响应.
在上边界,由于地形起伏的影响,采用向上延拓边界条件有一定的困难.在本研究中直接将空气层作为模型的一部分,用电导率为10-6S/m的高阻层来近似.数值模拟表明这种近似并不会对结果造成明显的影响.由于空气层的引入会导致空气层中的波动传播很远,因此,对于外边界,我们采用卷积完全匹配层(CPML)作为吸收边界.
3 算法验证
为了验证算法的有效性,我们在均匀半空间模型(图2,红实线为地下均匀介质与空气的界面)的地下介质内部引入虚拟的高斯地形界面(图2中黑实线所示),在图2中品红实线以下的均匀半空间采纳非正交网格.整个计算区域(包括品红线以上网格与底部网格)均采用非正交网格算法进行计算.非正交网格算法在正交网格中自动退化为常规的FDTD算法.在网格的底部,网格的划分是由非正交网格逐渐向最底层吸收边界的正交网格过渡得到.
考虑到实际测量时是记录z方向的电动势(即磁场Hz分量的响应),本文只针对Hz分量的结果进行讨论.图3给出了上述模型在虚拟地形界面处不同时刻的理论解(蓝实线)以及李墩柱的非正交FDTD算法[14](红实线)和本文提出的改进的非正交FDTD算法(淡蓝实线)的数值模拟结果.从图3可以看出,无论是李墩柱算法还是本文的改进算法的数值模拟结果都与理论解非常接近,两种数值算法的结果也很一致,表明非正交FDTD算法可以有效地模拟带地形的瞬变电磁场.
为了进一步考察本文提出的改进算法的效果,我们对图3的黑色矩形区域进行放大,如图4a所示.结果显示,与李墩柱算法的结果(红实线)相比,本文改进算法的结果(淡蓝实线)更接近于理论解(蓝实线),与理论解的误差分析结果(图4(b—d))也表明改进算法比李墩柱算法在精度方面有一定的提高.
4 数值计算结果与讨论
为简单起见,本文统一用高斯型的地形来近似各种地形模型,定义垂直方向的z坐标轴正方向向下,0点在地表,地形上任意点(x,y)的z坐标为:
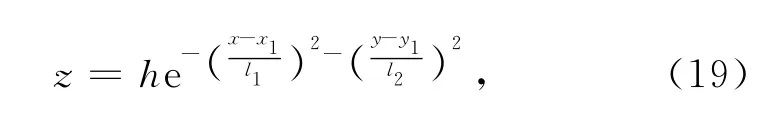
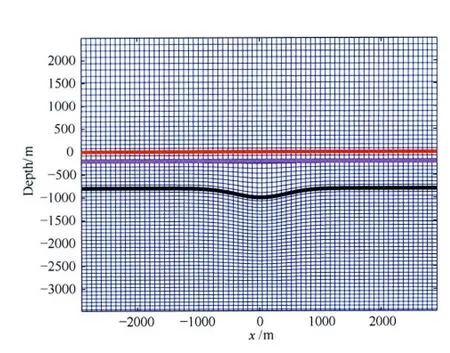
图2 带虚拟地形的均匀半空间模型的网格划分剖面图Fig.2 Gridding profile of a half-space model with a virtual topographical interface
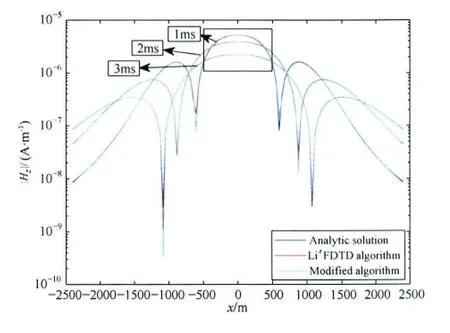
图3 带虚拟的200m山谷高斯地形界面的理论解以及非正交网格FDTD算法的数值模拟结果的对比Fig.3 Comparison of the analytical solution and the numerical results of the non-orthogonal FDTD method of a half-space model with a virtual topographical interface of a 200mdepth Gaussian-type subsurface
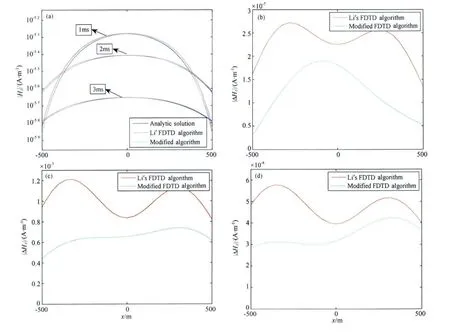
图4 (a)图3中矩形区域的放大图;(b)高斯界面处1ms两种非正交网格算法与理论解误差对比;(c)高斯界面处2ms两种非正交网格算法与理论解误差对比;(d)高斯界面处3ms两种非正交网格与理论解误差对比Fig.4 (a)The enlarged figure of the black rectangular region in Fig.3;Error comparison between Li′s FDTD method and modified FDTD method on the Gaussian-type subsurface(b)1ms,(c)2ms,(d)3ms
其中,点(x1,y1)为地形在地表的中心位置,h为地形深度(见图5a,即地形在点(x1,y1)的z值,正值表示山谷,负值表示山峰),宽度特征参数l1(见图5a)和l2(见图5b)分别为描述沿水平方向x和y的地形宽度特征的参数.
4.1 地形深度的影响
为了考察地形深度变化对瞬变电磁场的影响,我们令地形宽度特征参数l1和l2均为400m,图5a给出了深度分别为h1=100m,h2=200m,h3=300m和h4=400m的山谷模型的剖面示意图,源位于点(0,0,0),地形模型在地表的中心点相对源的距离|x1|为1600m,且在x轴负方向,地下介质电导率为10-2S/m,空气中电导率近似取为10-6S/m.
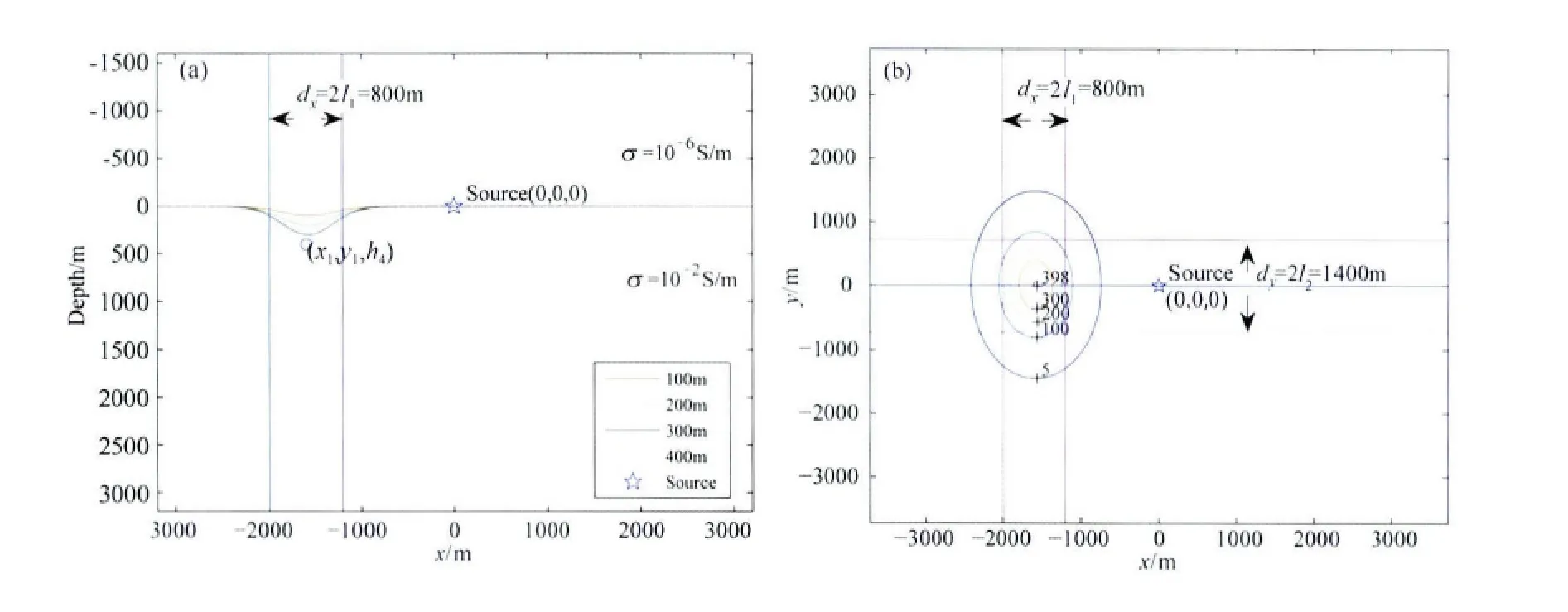
图5 (a)在半空间地表带高斯型山谷地形模型的剖面图;(b)半空间地表高斯型山谷地形俯视图Fig.5 (a)Vertical section of a half-space model with a Gaussian-type topography on the ground surface;(b)Cross-section of a Gaussian-type topographical model
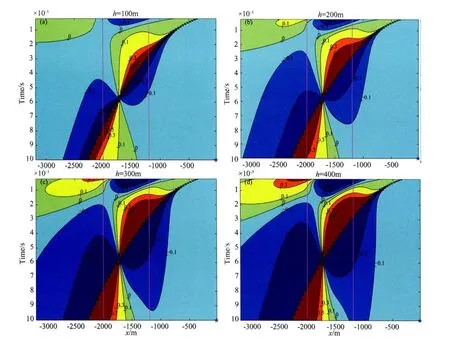
图6 基于图5a中的山谷模型计算得到的地形深度h对瞬变电磁场的归一化影响随时间的演化图(a)h=100m;(b)h=200m;(c)h=300m;(d)h=400m.Fig.6 Evolution of normalized influence due to the varied height,hof a topographical model
由于带地形情形下的场可以看作半空间的场与地形影响的叠加,为了定量描述地形对瞬变电磁场的影响,我们将带地形模型在地表的数值模拟结果减去半空间模型的相应结果,并计算其与半空间模型背景场的比值.作为一个例子,我们针对图5a所示的山谷模型进行了数值模拟,图6给出了地形深度对瞬变电磁场的归一化影响随时间演化的结果.图中地形的宽度由品红线标出,五角星指示源的位置.
图6表明,随着地形深度增加,地形对场的影响的强度和范围也逐渐变大,但影响的范围集中在地形附近.图中折线的产生是由于在“烟圈”附近的值很小,所以场的变化与背景场的比值很大,等值线变化比较密集.因此,折线的轨迹可以表示“烟圈”传播的轨迹.
为了进一步定量考察地形对瞬变电磁场的整体影响,我们基于图5a所示带地形模型计算得到的磁场Hz分量,并选择地形所在的x轴负半轴作为考察对象,按照以下公式计算地形整体影响相对于半空间模型理论解的归一化相对误差rn=其中,Hzm和Hzt分别代表带地形模型数值解和半空间模型理论解在x轴负半轴的值.图7给出了计算得到的地形深度的整体归一化影响随时间的变化曲线.
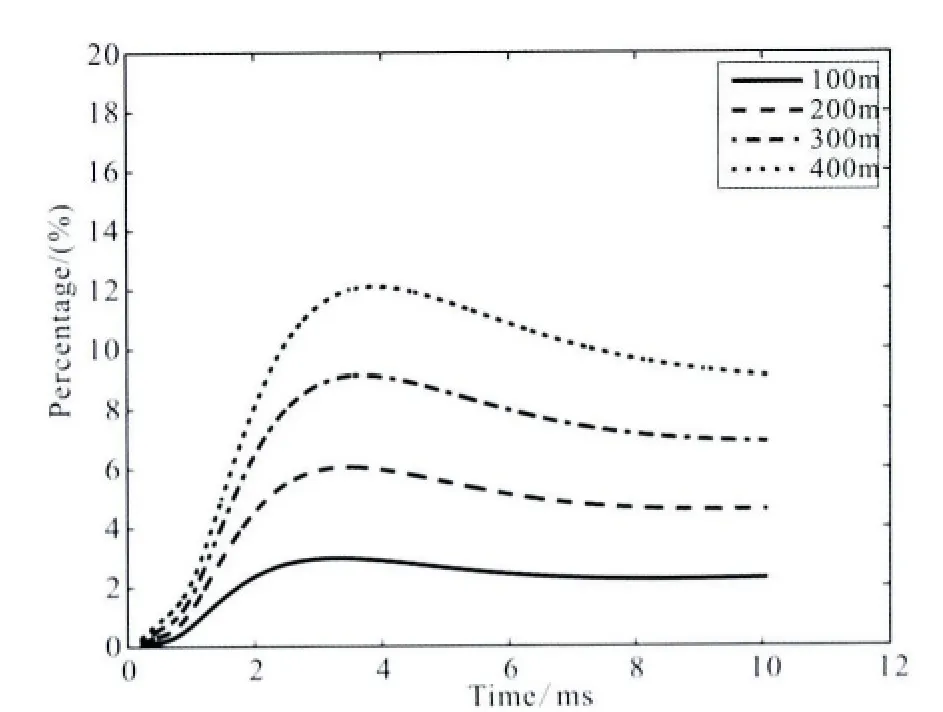
图7 不同时刻的地形深度整体的归一化影响Fig.7 Temporal variation of the total topographical effect normalized by a half-space model while the height of topography changes
沿x轴负半轴各点所受地形影响随时间演化结果(图6)表明,在早期,地形对垂直磁场的影响主要集中在地形附近.图7对地形整体效应的计算结果则显示,地形对场整体的影响在早期相对较小,这反映了场的主要能量此时还没有传过来;随着“烟圈”到达地形处,地形对场产生的整体影响相对较大,但其随时间增加的幅度逐渐趋于平缓,在一定程度上反映了地形的影响也随着场的衰减而减弱.图8给出了地形最低点处场值随时间的变化曲线.可以看出随着地形深度的增加,该点处场偏离半空间结果的幅度也相应地增加,这与地形整体的归一化影响相一致.
4.2 地形宽度的影响
由于本研究采用的是高斯型地形模型,其宽度的改变可以通过宽度特征参数l1和l2来控制.为方便起见,我们定义高斯型地形的宽度d为地形的两侧的深度减小为最大深度1/e处的距离,即x和y轴方向的宽度分别满足dx=2l1和dy=2l2(参见图5b的模型俯视图).为了考察地形宽度对瞬变电磁场的影响,作为具体的算例,保持源的位置、地形中心位置以及x轴方向的宽度等参数与图5a中400m山谷模型一致(亦即l1不变),令l2的取值从400m变化到700m(步长为100m),即相应y轴方向的宽度由800m变化到1400m(步长为200m).
类似图6的做法,我们将带地形模型在地表的数值模拟结果减去半空间模型的理论解,并相对半空间的理论解进行归一化.图9给出了y轴方向地形宽度变化模型对瞬变电磁场在x轴负半轴(x轴方向地形宽度由品红线标出)的归一化影响随时间的演化结果.
图9表明,尽管地形的y轴方向宽度由800m变化到1400m,地形对x轴负半轴的磁场垂直分量的影响范围和幅度并没有显著的变化.类似图7的做法,图10给出了地形y轴方向宽度变化对x轴负半轴磁场垂直分量的整体影响情况,结果显示,与地形深度相比,上述影响依旧不太显著.
4.3 地形与源距离变化的影响
考虑到源与地形中心的距离可能也是影响瞬变电磁场的相关因素之一,我们比较了相同地形(深度、宽度)条件下,源与地形中心距离改变时,地形模型对瞬变电磁场的影响.作为具体的算例,我们选择深度为400m的山谷模型,水平方向的两个宽度特征参数均为400m,令地形中心与源的距离分别为1600m,1720m,1840m和1960m.
从图11可以看出,“烟圈”抵达地形处的时间随着源与地形相对位置的增加而增加,地形的影响范围在“烟圈”到达地形处以前,主要集中在地形附近,几乎不随源与地形中心相对距离的变化而明显变化,但受影响的强度随之有所改变.随着“烟圈”抵达地形处,地形对瞬变电磁场的影响范围和强度都发生了变化.
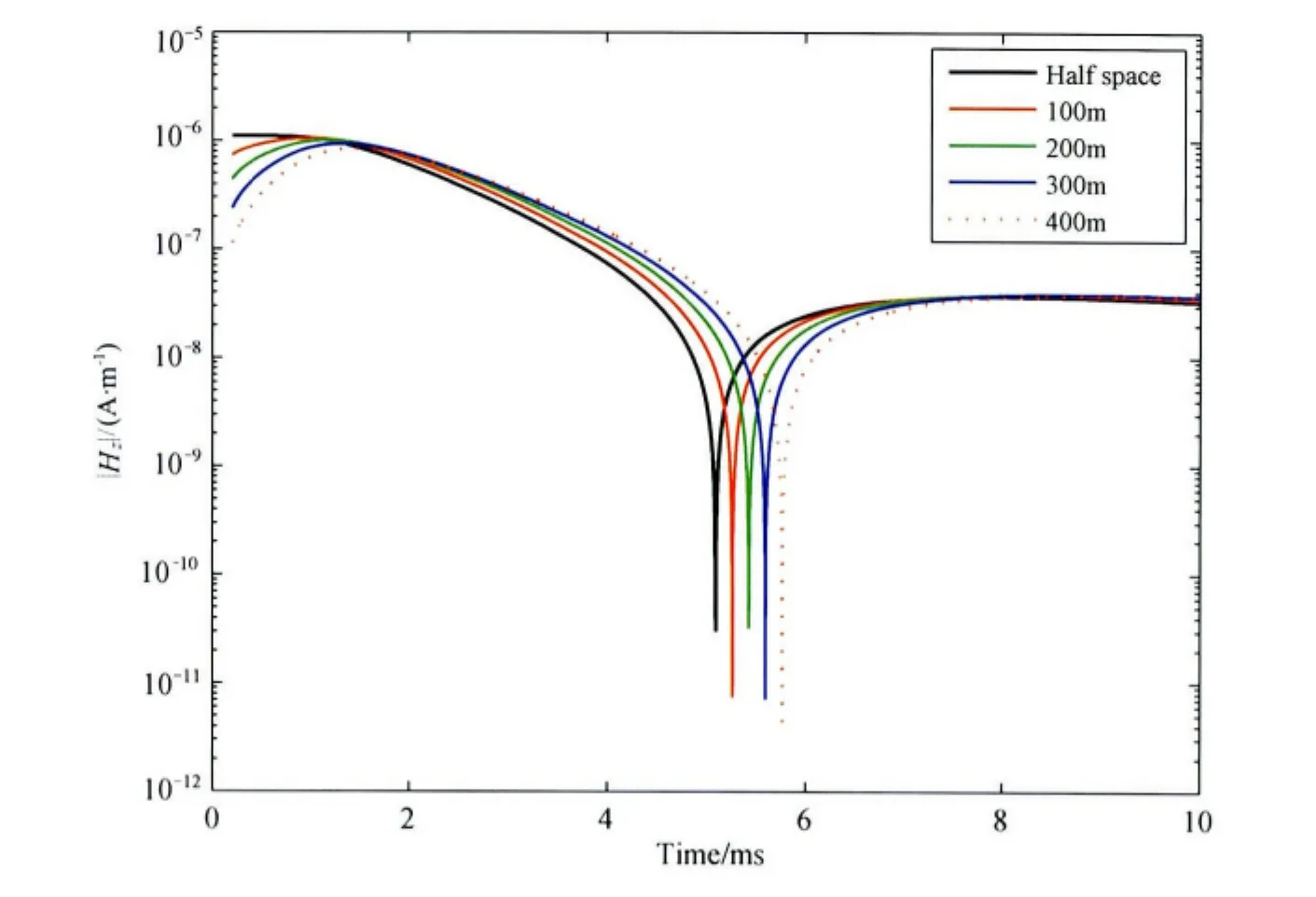
图8 不同地形深度的地形最低点处Hz分量随时间变化曲线Fig.8 Temporal variation of component Hzat the lowest point of topography while the height of topography changes

图9 y轴方向地形宽度dy对瞬变电磁场在x轴负半轴的归一化影响随时间的演化(a)dy=800m;(b)dy=1000m;(c)dy=1200m;(d)dy=1400m.Fig.9 Evolution of normalized influence due to a topographical model with a varied width(dy)along the y-axis
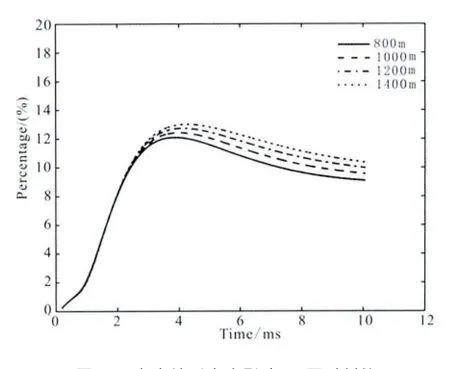
图10 考察地形宽度影响,不同时刻的地形整体的归一化影响Fig.10 Temporal variation of the total topographical effect normalized by a half-space model while the width of topography changes
图12给出了地形对瞬变电磁场的整体影响,结果反映源与地形相对位置的变化导致地形对瞬变电磁场的影响随时间而变化,不再是单调的影响.在早期,地形对场整体的影响相对有限,但随着场逐渐到达地形处,地形对场的整体影响逐渐增大,且随地形与源相对距离的增加而减小,这在一定程度上反映了地形对场整体的影响随着距离的增加而推迟.
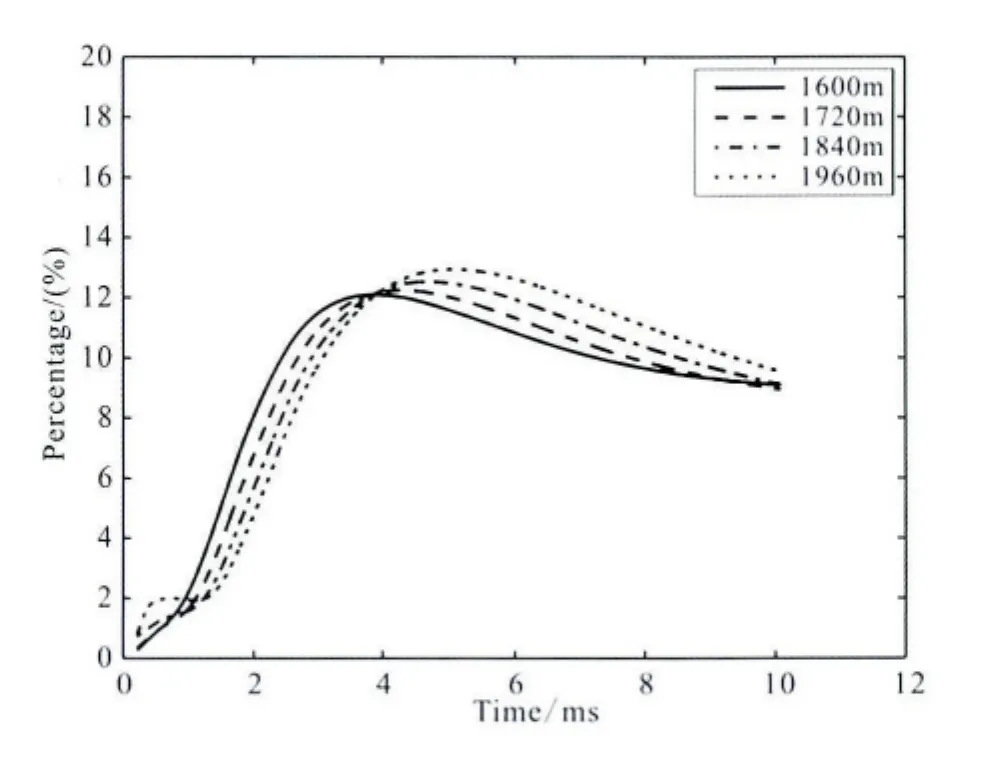
图12 考虑地形中心与源距离变化,不同时刻的地形整体的归一化影响Fig.12 Temporal variation of the total topographical effect of a topographical model with a varied distance from the source
5 结 论
本文的数值模拟研究表明,非正交网格可以有效地模拟带地形的瞬变电磁场,与以往带地形瞬变电磁正演中采纳的梯度网格和垂向变换网格相比,非正交网格更利于刻画精细的地形,从而提高算法精度.本文提出的采用非等权投影的改进非正交网格FDTD算法,进一步提高了带地形瞬变电磁场三维正演算法的精度.
利用我们提出的改进非正交网格FDTD算法,对不同地形模型进行了数值模拟,结果表明,地形的深度、宽度以及地形与源的相对位置等都可能影响瞬变电磁场的测量结果,但影响程度不一.瞬变电磁场的地形响应与地形的深度存在正相关,而宽度的影响可能与测线方向和宽度变化方向有关,地形与源的相对位置变化对瞬变电磁场的影响随时间并非单调变化,但随着“烟圈”的抵达时间推后,地形对瞬变电磁场归一化影响效果也相应地延迟.
致 谢 感谢两位审稿专家提出建设性修改意见.
(
)
[1] Mitsuhata Y.2-D electromagnetic modeling by finite-element method with a dipole source and topography.Geophysics,2000,65(2):465-475.
[2] 肖明顺.带地形的瞬变电磁2.5维有限元数值模拟研究[硕士论文].北京:中国地质大学,2008.Xiao M S.Study on 2.5Dnumerical modeling for transient electromagnetic method by finite element method with topography[Master′s thesis](in Chinese).Beijing:China University of Geosciences,2008.
[3] Sugeng F.Modeling the 3DTDEM response using the 3D full-domain finite-element method based on the hexahedral edge-element technique.ExplorationGeophysics,1998,29(4):615-619.
[4] Li J H,Zhu Z Q,Liu S C,et al.3Dnumerical simulation for the transient electromagnetic field excited by the central loop based on the vector finite-element method.Journalof GeophysicsandEngineering,2011,8(4):560-567.
[5] Xiong B.2.5Dforward for the transient electromagnetic response of a block linear resistivity distribution.Journalof GeophysicsandEngineering,2011,8(1):115-121.
[6] 唐新功,胡文宝,严良俊.地堑地形对长偏移距瞬变电磁测深的影响研究.工程地球物理学报,2004,1(4):313-317.Tang X G,Hu W B,Yan L J.Graben topographyic effects to the long offset transient electromagnetic responses.ChineseJournalofEngineeringGeophysics(in Chinese),2004,1(4):313-317.
[7] 唐新功,胡文宝,严良俊.瞬变电磁法对存在山谷地形时的多个异常体的探测能力研究.地震地质,2005,27(2):316-323.Tang X G,Hu W B,Yan L J.The detectability of transient electromagnetic method to multiple 3Dbodies with valley topography.SeismologyandGeology(in Chinese),2005,27(2):316-323.
[8] Tang X G,Hu W B,Yan L J.Topographic effects on long offset transient electromagnetic response.AppliedGeophysics,2011,8(4):277-284.
[9] 唐新功,胡文宝,严良俊.斜坡和垂直断层地形的瞬变电磁响应.石油天然气学报,2011,33(10):57-60.Tang X G,Hu W B,Yan L J.The transient electromagnetic responses of slope and vertical fault topography.Journalof OilandGasTechnology(in Chinese),2011,33(10):57-60.
[10] Zhdanov M S,Lee S K,Yoshioka K.Integral equation method for 3Dmodeling of electromagnetic fields in complex structures with inhomogeneous background conductivity.Geophysics,71(6):G333-G345.
[11] Commer M,Newman G.A parallel finite-difference approach for 3Dtransient electromagnetic modeling with galvanic sources.Geophysics,2004,69(5):1192-1202.
[12] Endo M,Noguchi K.Chapter 6three-dimensional modeling considering the topography for the case of time-domain electromagnetic method.MethodsinGeochemistryand Geophysics,2002,35:85-107.
[13] 肖怀宇.带地形的瞬变电磁法三维数值模拟研究[硕士论文].北京:中国地质大学,2006.Xiao H Y.Three-dimensional numerical modeling considering the topography of TEM[Master′s thesis](in Chinese).Beijing:China University of Geosciences,2006.
[14] 李墩柱.用正交网格模拟带地形的瞬变电磁场[硕士论文].北京:北京大学,2010.Li D Z.TEM simulation with topography using nonorthogonal grid FDTD[Master′s thesis](in Chinese).Beijing:Peking University,2010.
[15] Wang T,Hohmann G W.A finite-difference,time-domain solution for 3-dimensional electromagnetic modeling.Geophysics,1993,58(6):797-809.
[16] 许洋铖,林君,李肃义等.全波形时间域航空电磁响应三维有限差分数值计算.地球物理学报,2012,55(6):2105-2114.Xu Y C,Lin J,Li S Y,et al.Calculation of full-waveform airborne electromagnetic response with three-dimension finitedifference solution in time-domain.ChineseJ.Geophys.(in Chinese),2012,55(6):2105-2114.
[17] 孙怀凤,李貅,李术才等.考虑关断时间的回线源激发TEM三维时域有限差分正演.地球物理学报,2013,56(3):1049-1064.Sun H F,Li X,Li S C,et al.Three-dimensional FDTD modeling of TEM excited by a loop source considering ramp time.ChineseJ.Geophys.(in Chinese),2013,56(3):1049-1064.
[18] Du Fort E C,Frankel S P.Stability conditions in the numerical treatment of parabolic differential equations.MathematicalTablesandOtherAidstoComputation,1953,7(43):135-152.
[19] Holland R.Finite-difference solution of Maxwell′s equations in generalized nonorthogonal Coordinates.IEEETransactionson NuclearScience,1983,30(6):4589-4591.
[20] Lee J F,Palandech R,Mittra R.Modeling three-dimensional discontinuities in waveguides using nonorthogonal FDTD algorithm.IEEETransactionsonMicrowaveTheoryand Techniques,1992,40(2):346-352.
[21] Yee K S.Numerical solution of initial boundary value problems involving Maxwell′s equations in isotropic media.IEEETransactionsonAntennasandPropagation,1966,14(3):302-307.
[22] 陈丹丹.瞬变电磁法三维正演研究[硕士论文].北京:中国地质大学,2008.Chen D D.Study of three-dimensional forward of TEM[Master′s thesis](in Chinese).Beijing:China University of Geosciences,2008.

